Lý thuyết
Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Công thức
Công thức Toán học
Soạn văn
Toán THPT
Toán THCS
Thi vào lớp 10
Tuyển sinh
Đại học
Bản tin
Thư viện câu hỏi
Thi Online
Hỏi bàiKhảo sát sự biến thiên và vẽ đồ thị của hàm số (hàm phân thức hữu tỷ)
1. Kiến thức cần nhớ
Cho hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\)
* Tập xác định \(D = R\backslash \left\{ {\dfrac{{ - d}}{c}} \right\}\)
* Sự biến thiên
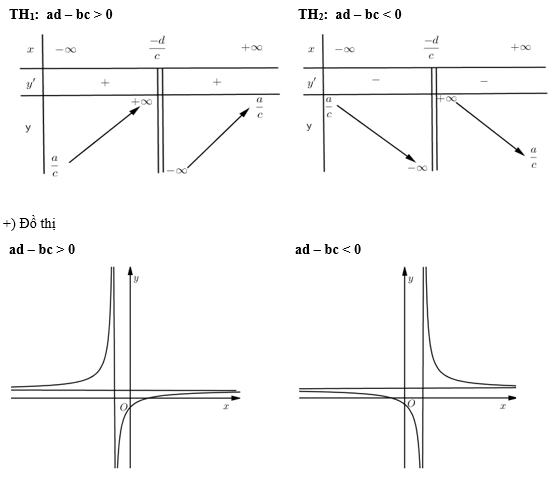
+) \(y' = \dfrac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}\)
+) Đường tiệm cận: tiệm cận đứng \(x = - \dfrac{d}{c}\); tiệm cận ngang \(y = \dfrac{a}{c}\).
+) Tâm đối xứng \(I\left( { - \dfrac{d}{c};\dfrac{a}{c}} \right)\).
+) Bảng biến thiên :
2. Các dạng toán thường gặp
Phương pháp:
- Bước 1: Tìm các tiệm cận đứng, tiệm cận ngang của đồ thị hàm số đã cho.
+ Tiệm cận đứng là đường thẳng \(x = {x_0}\) song song với trục \(Oy\), khi đó \({x_0}\) là nghiệm của mẫu thức.
+ Tiệm cận ngang là đường thẳng \(y = {y_0}\) song song với trục \(Ox\), khi đó \({y_0} = \dfrac{a}{c}\).
- Bước 2: Tìm giao điểm của đồ thị hàm số với hai trục tọa độ.
+ Giao điểm của đồ thị với trục \(Oy\) là \(\left( {0;\dfrac{b}{d}} \right)\).
+ Giao điểm của đồ thị với trục \(Ox\) là \(\left( { - \dfrac{b}{a};0} \right)\).
- Bước 3: Xét tính đơn điệu của hàm số.
+ Hai nhánh đồ thị hướng lên từ trái qua phải thì hàm số đồng biến \( \Leftrightarrow ad - bc > 0\).
+ Hai nhánh đồ thị hướng xuống từ trái qua phải thì hàm số nghịch biến \( \Leftrightarrow ad - bc < 0\).
Khi thực hành, HS có thể áp dụng từng bước để loại trừ đáp án, đến khi chọn được đáp án đúng thì kết luận, không nhất thiết phải thực hiện cả 3 bước nếu đã có được đáp án.
Phương pháp:
- Bước 1: Tìm các tiệm cận của đồ thị hàm số.
+ Tại điểm \({x_0}\) mà \(\mathop {\lim }\limits_{x \to x_0^ - } y = \pm \infty \) hoặc \(\mathop {\lim }\limits_{x \to x_0^ + } y = \pm \infty \) thì \(x = {x_0}\) là tiệm cận đứng của đồ thị hàm số, khi đó \({x_0}\) là nghiệm của mẫu thức.
+ Nếu có \(y = {y_0}\) tại điểm \(x = \pm \infty \) thì \(y = {y_0}\) là tiệm cận ngang của đồ thị hàm số, khi đó \({y_0} = \dfrac{a}{c}\).
- Bước 2: Xét tính đơn điệu của hàm số.
+ Nếu trên cả 2 khoảng \(\left( { - \infty ;{x_0}} \right)\) và \(\left( {{x_0}; + \infty } \right)\), đạo hàm đều mang dấu \( + \) thì hàm số đồng biến trên 2 khoảng đó, khi đó \(ad - bc > 0\).
+ Nếu trên cả 2 khoảng \(\left( { - \infty ;{x_0}} \right)\) và \(\left( {{x_0}; + \infty } \right)\), đạo hàm đều mang dấu \( - \) thì hàm số nghịch biến trên 2 khoảng đó, khi đó \(ad - bc < 0\).