Cực trị của hàm số

1. Các kiến thức cần nhớ

a) Cần phân biệt các các khái niệm:

- Điểm cực trị \({x_0}\) của hàm số.

- Giá trị cực trị của hàm số.

- Điểm cực trị \(\left( {{x_0};{y_0}} \right)\) của đồ thị hàm số.

b) Nếu \(y = f\left( x \right)\) có đạo hàm trên \(\left( {a;b} \right)\) và đạt cực trị tại \({x_0} \in \left( {a;b} \right)\) thì \(f'\left( {{x_0}} \right) = 0\).

Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng \(K = \left( {{x_0} - h;{x_0} + h} \right)\) và có đạo hàm trên \(K\) hoặc \(K\backslash \left\{ {{x_0}} \right\}\left( {h > 0} \right)\).

a) Nếu \(\left\{ \begin{array}{l}f'\left( x \right) > 0,\forall x \in \left( {{x_0} - h} \right)\\f'\left( x \right) < 0,\forall x \in \left( {{x_0} + h} \right)\end{array} \right.\)  thì \({x_0}\) là một điểm cực đại của hàm số.

b) Nếu \(\left\{ \begin{array}{l}f'\left( x \right) < 0,\forall x \in \left( {{x_0} - h} \right)\\f'\left( x \right) > 0,\forall x \in \left( {{x_0} + h} \right)\end{array} \right.\)  thì \({x_0}\) là một điểm cực tiểu của hàm số.

Hàm số có thể đạt cực trị tại những điểm mà tại đó đạo hàm không xác định.

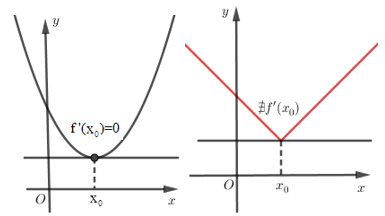
Giả sử \(y = f\left( x \right)\) có đạo hàm cấp 2 trong \(\left( {{x_0} - h;{x_0} + h} \right)\left( {h > 0} \right)\).

a) Nếu \(\left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) > 0\end{array} \right.\) thì \({x_0}\) là một điểm cực tiểu của hàm số.

b) Nếu \(\left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) < 0\end{array} \right.\) thì \({x_0}\) là một điểm cực đại của hàm số.

2. Tìm cực trị của hàm số

Phương pháp:

Có thể tìm cực trị của hàm số bởi một trong hai quy tắc sau:

- Bước 1: Tìm tập xác định của hàm số.

- Bước 2: Tính \(f'\left( x \right)\), tìm các điểm tại đó \(f'\left( x \right) = 0\) hoặc không xác định.

- Bước 3: Lập bảng biến thiên và kết luận.

+ Tại các điểm mà đạo hàm đổi dấu từ âm sang dương thì đó là điểm cực tiểu của hàm số.

+ Tại các điểm mà đạo hàm đổi dấu từ dương sang âm thì đó là điểm cực đại của hàm số.

- Bước 1: Tìm tập xác định của hàm số.

- Bước 2: Tính \(f'\left( x \right)\), giải phương trình \(f'\left( x \right) = 0\) và kí hiệu \({x_1},...,{x_n}\) là các nghiệm của nó.

- Bước 3: Tính \(f''\left( x \right)\) và \(f''\left( {{x_i}} \right)\).

- Bước 4: Dựa và dấu của \(f''\left( {{x_i}} \right)\) suy ra điểm cực đại, cực tiểu:

+ Tại các điểm \({x_i}\) mà \(f''\left( {{x_i}} \right) > 0\) thì đó là điểm cực tiểu của hàm số.

+ Tại các điểm \({x_i}\) mà \(f''\left( {{x_i}} \right) < 0\) thì đó là điểm cực đại của hàm số.

Đối với các bài toán tìm cực trị của hàm số lượng giác thì dùng quy tắc 2 sẽ thuận tiện hơn, tránh được việc xét dấu đạo hàm.