Đồ thị của hàm số và phép tịnh tiến hệ tọa độ

Lý thuyết về đồ thị hàm số và phép tịnh tiến hệ tọa độ môn toán lớp 12 với nhiều dạng bài cùng phương pháp giải nhanh kèm bài tập vận dụng
(445) 1483 26/07/2022
Bài viết đã được lưu

Nội dung bài viết

    Xem thêm

    1. Các kiến thức cần nhớ

    Công thức tịnh tiến hệ tọa độ:

    Cho điểm I(x0;y0),M(x;y) đối với hệ tọa độ Oxy

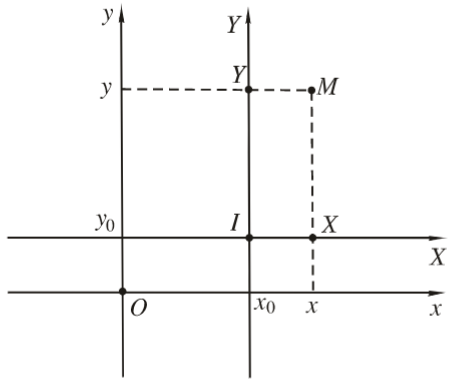
    Công thức chuyển hệ tọa độ trong phép tịnh tiến theo véc tơ →OI là: {x=X+x0y=Y+y0

    Khi đó điểm I(0;0),M(X,Y) đối với hệ tọa độ IXY

    Phương trình đường cong trong hệ tọa độ mới:

    Cho đường cong (C):y=f(x) trong hệ tọa độ Oxy, khi đó phương trình của (C) trong hệ tọa độ IXY là:

    Y=f(X+x0)−y0

    Tâm đối xứng của đồ thị hàm số:

    Nếu hàm số Y=g(X) là hàm số lẻ (trong hệ tọa độ mới IXY) thì điểm I(x0;y0) trong hệ tọa độ Oxy là tâm đối xứng của đồ thị hàm số y=f(x)

    2. Một số dạng toán thường gặp

    Dạng 1: Tìm công thức chuyển hệ tọa độ.

    Phương pháp:

    - Bước 1: Tính tọa độ điểm I (nếu cần).

    - Bước 2: Viết công thức chuyển hệ tọa độ {x=X+x0y=Y+y0

    Dạng 2: Viết phương trình đường cong sau khi chuyển hệ tọa độ.

    Phương pháp:

    - Bước 1: Tìm tọa độ điểm I (nếu cần)

    - Bước 2: Viết công thức chuyển hệ tọa độ {x=X+x0y=Y+y0

    - Bước 3: Viết phương trình đường cong đối với hệ tọa độ mới: Y=f(X+x0)−y0

    Dạng 3: Tìm tâm đối xứng của đồ thị hàm số y=ax+bcx+d(ad−bc≠0)

    Phương pháp:

    - Bước 1: Tìm tọa độ điểm I: {x0=−dcy0=ac

    - Bước 2: Viết công thức chuyển hệ tọa độ {x=X+x0y=Y+y0

    - Bước 3: Viết phương trình đường cong đối hệ tọa độ mới: Y=f(X+x0)−y0.

    - Bước 4: Chứng minh g(−X)=−g(X)=−Y suy ra hàm số Y=g(X) là hàm số lẻ và kết luận.

    Dạng 4: Tìm tâm đối xứng của đồ thị hàm số bậc ba.

    Phương pháp:

    - Bước 1: Tính y′,y″, giải phương trình y'' = 0 tìm nghiệm {x_0} \Rightarrow điểm I\left( {{x_0};{y_0}} \right)

    - Bước 2: Viết công thức chuyển hệ tọa độ \left\{ \begin{array}{l}x = X + {x_0}\\y = Y + {y_0}\end{array} \right.

    - Bước 3: Viết phương trình đường cong đối hệ tọa độ mới: Y = f\left( {X + {x_0}} \right) - {y_0}.

    - Bước 4: Chứng minh g\left( { - X} \right) =  - g\left( X \right) =  - Y suy ra hàm số Y = g\left( X \right) là hàm số lẻ và kết luận.

    Xem toàn bộ nội dung Toán 12:

    (445) 1483 26/07/2022
    Bài viết đã được lưu
    Bài trước
    Bài sau  
    Tìm thêm: Lý thuyết Lý Thuyết Lớp 12 Toán 12