Hàm số logarit

- Hàm số logarit cơ số \(a\) là hàm số có dạng \(y = {\log _a}x\left( {0 < a \ne 1} \right)\).

- Hàm số logarit có đạo hàm tại \(\forall x > 0\) và \(y' = \left( {{{\log }_a}x} \right)' = \dfrac{1}{{x\ln a}}\)

(đặc biệt \(\left( {\ln x} \right)' = \dfrac{1}{x}\) )

- Giới hạn liên quan \(\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln \left( {1 + x} \right)}}{x} = 1\).

- Đạo hàm: \(y = {\log _a}x \Rightarrow y' = \left( {{{\log }_a}x} \right)' = \dfrac{1}{{x\ln a}};y = {\log _a}u\left( x \right) \Rightarrow y' = \dfrac{{u'\left( x \right)}}{{u\left( x \right)\ln a}}\)

(đặc biệt \(\left( {\ln x} \right)' = \dfrac{1}{x}\) )

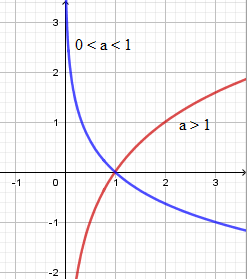
Khảo sát \(y = {\log _a}x\):

- TXĐ: \(D = \left( {0; + \infty } \right)\)

- Chiều biến thiên:

+ Nếu \(a > 1\) thì hàm đồng biến trên \(\left( {0; + \infty } \right)\).

+ Nếu \(0 < a < 1\) thì hàm nghịch biến trên \(\left( {0; + \infty } \right)\).

- Đồ thị:

+ Đồ thị hàm số có tiệm cận đứng \(x = 0\).

+ Đồ thị hàm số luôn đi qua các điểm \(\left( {1;0} \right)\) và \(\left( {a;1} \right)\).

+ Đồ thị nằm hoàn toàn phía bên phải trục tung vì \(x > 0\).

+ Dáng đồ thị:

Dạng 1: Tìm tập xác định của hàm số.

Phương pháp:

- Bước 1: Tìm điều kiện để các logarit xác định.

Hàm số \({\log _a}\left( {u\left( x \right)} \right)\) xác định \(\left\{ \begin{array}{l}a > 0\\u\left( x \right) > 0\end{array} \right.\)

- Bước 2: Tìm điều kiện để các biểu thức dưới dấu căn bậc hai, biểu thức dưới mẫu trong các phân thức,…(nếu có).

+ Căn bậc hai \(\sqrt {u\left( x \right)} \) xác định nếu \(u\left( x \right) \ge 0\).

+ Phân thức \(\dfrac{{u\left( x \right)}}{{v\left( x \right)}}\) xác định nếu \(g\left( x \right) \ne 0\).

- Bước 3: Giải các bất phương trình ở trên và kết hợp nghiệm ta được tập xác định của hàm số.

Dạng 2: Tìm hàm số có đồ thị cho trước và ngược lại.

Phương pháp:

- Bước 1: Quan sát dáng đồ thị, tính đơn điệu,…của các đồ thị bài cho.

- Bước 2: Đối chiếu với hàm số bài cho và chọn kết luận.

Dạng 3: Tìm mối quan hệ giữa các cơ số khi biết đồ thị.

Phương pháp:

- Bước 1: Quan sát các đồ thị, nhận xét về tính đơn điệu để nhận xét các cơ số.

+ Hàm số đồng biến thì cơ số lớn hơn \(1\).

+ Hàm số nghịch biến thì cơ số lớn hơn \(0\) và nhỏ hơn \(1\).

- Bước 2: So sánh các cơ số dựa vào phần đồ thị của hàm số.

- Bước 3: Kết hợp các điều kiện ở trên ta được mối quan hệ cần tìm.

Dạng 4: Tính đạo hàm các hàm số.

Phương pháp:

- Bước 1: Áp dụng các công thức tính đạo hàm của tổng, hiệu, tích, thương để tính đạo hàm hàm số đã cho.

\(\left( {u \pm v} \right)' = u' \pm v';\left( {uv} \right)' = u'v + uv';\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}\)

- Bước 2: Tính đạo hàm các hàm số thành phần dựa vào công thức tính đạo hàm các hàm số cơ bản: hàm đa thức, phân thức, hàm mũ, logarit, lũy thừa,…

- Bước 3: Tính toán và kết luận.

Dạng 5: Tính giới hạn các hàm số.

Phương pháp:

Áp dụng các công thức tính giới hạn đặc biệt để tính toán:

 \(\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln \left( {1 + x} \right)}}{x} = 1\) ; \(\mathop {\lim }\limits_{x \to 0} \dfrac{{{{\log }_a}\left( {1 + x} \right)}}{x} = \dfrac{1}{{\ln a}}\)

Dạng 6: Tìm GTLN, GTNN của hàm số mũ và hàm số logarit trên một đoạn.

Phương pháp:

- Bước 1: Tính \(y'\), tìm các nghiệm \({x_1},{x_2},...,{x_n} \in \left[ {a;b} \right]\) của phương trình \(y' = 0\).

- Bước 2: Tính \(f\left( a \right),f\left( b \right),f\left( {{x_1}} \right),...,f\left( {{x_n}} \right)\).

- Bước 3: So sánh các giá trị vừa tính ở trên và kết luận GTLN, GTNN của hàm số.

+ GTNN \(m\) là số nhỏ nhất trong các giá trị tính được.

+ GTLN \(M\) là số lớn nhất trong các giá trị tính được.