Khái niệm về khối đa diện (sự bằng nhau của các khối đa diện)

Lý thuyết về phép đối xứng qua mặt phẳng và sự bằng nhau của các khối đa diện môn toán lớp 12 với nhiều dạng bài cùng phương pháp giải nhanh kèm bài tập vận dụng
(422) 1406 26/07/2022
Bài viết đã được lưu

Nội dung bài viết

    Xem thêm

    1. Phép đối xứng qua mặt phẳng

    - Định nghĩa: Phép đối xứng qua mặt phẳng (P) là phép biến hình biến mỗi điểm thuộc (P) thành chính nó và biến mỗi điểm M không thuộc (P) thành điểm M′ sao cho (P) là mặt phẳng trung trực của MM′.

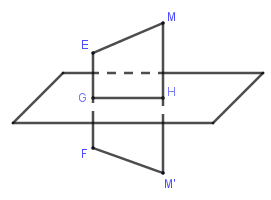
    - Phép đối xứng qua mặt phẳng bảo toàn khoảng cách giữa 2 điểm bất kì.

    2. Mặt phẳng đối xứng của một hình

    - Định nghĩa: Nếu phép đối xứng qua mặt phẳng (P) biến hình H thành chính nó thì (P) gọi là mặt phẳng đối xứng của hình H.

    Một số hình có mặt phẳng đối xứng: mặt cầu, tứ diện đều, hình lập phương, hình bát diện đều,…

    3. Hai hình bằng nhau

    a) Phép dời hình

    - Phép biến hình F được gọi là phép dời hình nếu nó bảo toàn khoảng cách giữa hai điểm bất kì, nghĩa là nếu F biến hai điểm M,N thành M′,N′ thì M′N′=MN.

    - Phép dời hình biến đường thẳng thành đường thẳng, mặt phẳng thành mặt phẳng,…

    - Hợp thành của những phép dời hình là phép dời hình.

    Ví dụ:  Phép đồng nhất, phép đối xứng qua mặt phẳng, phép đối xứng trục, đối xứng tâm, phép tịnh tiến,…

    b) Hai hình bằng nhau

    - Định nghĩa: Hai hình H và H′ được gọi là bằng nhau nếu tồn tại một phép dời hình biến hình này thành hình kia.

    - Định lý: Hai tứ diện bằng nhau nếu chúng có các cạnh tương ứng bằng nhau.

    + Hai tứ diện đều bằng nhau nếu chúng có các cạnh bằng nhau.

    + Hai hình lập phương bằng nhau nếu chúng có cạnh bằng nhau.

    Xem toàn bộ nội dung Toán 12:

    (422) 1406 26/07/2022
    Bài viết đã được lưu
    Bài trước
    Bài sau  
    Tìm thêm: Lý thuyết Lý Thuyết Lớp 12 Toán 12