Hệ tọa độ trong không gian

Lý thuyết về hệ tọa độ trong không gian – tọa độ điểm môn toán lớp 12 với nhiều dạng bài cùng phương pháp giải nhanh kèm bài tập vận dụng
(397) 1322 23/09/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    1. Hệ tọa độ trong không gian

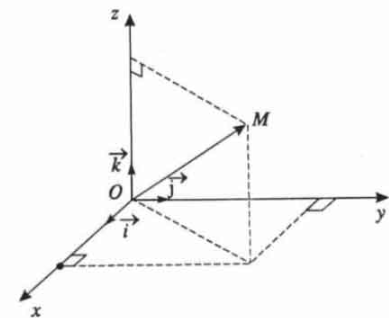
    - Hệ trục tọa độ \(Oxyz\) với các véc tơ đơn vị trên các trục \(Ox,Oy,Oz\) theo thứ tự là \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \)  với:

    \(\left| {\overrightarrow i } \right| = \left| {\overrightarrow j } \right| = \left| {\overrightarrow k } \right| = 1\) hoặc \({\overrightarrow i ^2} = {\overrightarrow j ^2} = {\overrightarrow k ^2} = 1\) và \(\overrightarrow i .\overrightarrow j  = \overrightarrow j .\overrightarrow k  = \overrightarrow k .\overrightarrow i  = 0\)

    - Các trục tọa độ \(Ox\): trục hoành; \(Oy\): trục tung; \(Oz\): trục cao.

    - Các mặt phẳng tọa độ: \(\left( {Oxy} \right),\left( {Oyz} \right),\left( {Ozx} \right)\).

    2. Tọa độ điểm trong không gian

    - Điểm \(M\left( {x;y;z} \right) \Leftrightarrow \overrightarrow {OM}  = x.\overrightarrow i  + y.\overrightarrow j  + z.\overrightarrow k \)

    - Nếu \(I;J;K\) là hình chiếu của \(M\) lên các trục \(Ox,Oy,Oz\) thì \(I\left( {x;0;0} \right),J\left( {0;y;0} \right),K\left( {0;0;z} \right),\) \(x = \overline {OI} ,y = \overline {OJ} ,z = \overline {OK} \).

    - Nếu \(D;E;F\) là hình chiếu của \(M\) lên các mặt phẳng tọa độ \(\left( {Oxy} \right),\left( {Oyz} \right),\left( {Ozx} \right)\) thì \(D\left( {x;y;0} \right),E\left( {0;y;z} \right),F\left( {x;0;z} \right)\).

    Khi chiếu một điểm lên các trục tọa độ hoặc mặt phẳng tọa độ thì ta có thể nhớ theo quy tắc: “Chiếu lên cái gì thì giữ nguyên cái đó, còn lại cho bằng \(0\)”.

    - Tọa độ trung điểm đoạn thẳng \(AB\) là \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2}} \right)\)

    - Tọa độ trọng tâm tam giác \(ABC\) là \(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3}} \right)\)

    - Tọa độ trọng tâm tứ diện \(ABCD\) là \(( {\frac{{{x_A} + {x_B} + {x_C} + {x_D}}}{4};\frac{{{y_A} + {y_B} + {y_C} + {y_D}}}{4};\frac{{{z_A} + {z_B} + {z_C} + {z_D}}}{4}}) \)

    Xem toàn bộ nội dung Toán 12:

    (397) 1322 23/09/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý Thuyết Lớp 12 Toán 12