Đề kiểm tra học kì 1 - Đề số 2
-
Hocon247
-
50 câu hỏi
-
90 phút
-
654 lượt thi
-
Dễ
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Tìm tập nghiệm S của phương trình: ${4^{x + 1}} + {4^{x - 1}} = 272$
Thử lần lượt từng đáp án ta thấy $x = 3$ là nghiệm của phương trình
Hướng dẫn giải:
Với câu hỏi có 4 đáp án chỉ có 1 giá trị nghiệm, ta thử ngay từng đáp án vào phương trình đã cho.
Giải thích thêm:
Cách giải trực tiếp:
$\begin{array}{l}
{4^{x + 1}} + {4^{x - 1}} = 272\\
\Leftrightarrow {4.4^x} + \frac{{{4^x}}}{4} = 272\\
\Leftrightarrow {16.4^x} + {4^x} - 1088 = 0\\
\Leftrightarrow {17.4^x} = 1088\\
\Leftrightarrow {4^x} = 64 = {4^3}\\
\Leftrightarrow x = 3
\end{array}$
Phép đối xứng qua mặt phẳng \(\left( P \right)\) biến điểm \(M,N\) thành \(M',N'\) thì:
Phép đối xứng qua mặt phẳng bảo toàn khoảng cách giữa 2 điểm bất kì nên \(M'N' = MN\).
Hướng dẫn giải:
Sử dụng tính chất phép đối xứng qua mặt phẳng bảo toàn khoảng cách của hai điểm.
Giải thích thêm:
Một số em có thể sẽ chọn đáp án B vì xác định nhầm khoảng các giữa hai điểm.
Các em cần chú ý phân biệt kí hiệu “$=$” và “\( \equiv \)”, hai đoạn thẳng bằng nhau không có nghĩa là chúng trùng nhau.
Công thức nào sau đây không đúng khi tính diện tích toàn phần hình trụ?
Ta có: \({S_{tp}} = {S_{xq}} + 2{S_d} = 2\pi rh + 2\pi {r^2} = 2\pi r\left( {h + r} \right) = {C_d}.\left( {h + r} \right)\)
Dó đó công thức ở đáp án D là sai.
Hướng dẫn giải:
Sử dụng công thức tính diện tích toàn phần hình trụ \({S_{tp}} = {S_{xq}} + 2{S_d} = 2\pi rh + 2\pi {r^2}\).
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án C vì không nhớ rõ công thức tính chu vi đường tròn và diện tích toàn phần hình trụ.
Anh A mua nhà trị giá ba trăm triệu đồng theo phương thức trả góp. Nếu cuối mỗi tháng, bắt đầu từ tháng thứ nhất anh A trả 5.500.000đ và chịu lãi suất tiền chưa trả là 0,5%/tháng thì sau bao nhiêu tháng anh A trả hết số tiền trên.
Áp dụng công thức trả góp ta có:
\(\begin{array}{l}\,\,\,\,\,\,T{\left( {1 + r} \right)^n} = \dfrac{A}{r}\left[ {{{\left( {1 + r} \right)}^n} - 1} \right]\\ \Leftrightarrow 300{\left( {1 + 0,5\% } \right)^n} = \dfrac{{5,5}}{{0,5\% }}\left[ {{{\left( {1 + 0,5\% } \right)}^n} - 1} \right]\\ \Leftrightarrow 800.1,{005^n} = 1100\\ \Leftrightarrow n = {\log _{1,005}}\dfrac{{1100}}{{800}} \approx 63,85\end{array}\)
Vậy sau ít nhất 64 tháng anh A mới trả hết số tiền 300 triệu.
Hướng dẫn giải:
Sử dụng công thức trả góp.
\(T = \dfrac{{A\left[ {{{\left( {1 + r} \right)}^n} - 1} \right]}}{{r{{\left( {1 + r} \right)}^n}}}\) , trong đó:
$T:$ Số tiền vay ban đầu
$A:$ Số tiền trả hàng kì
$r:$ lãi suất
$n:$ số kì hạn.
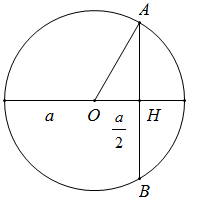
Cho hình trụ có bán kính đáy bằng \(a\). Cắt hình trụ bởi một mặt phẳng song song với trục của hình trụ và cách trục của hình trụ một khoảng bằng \(\dfrac{a}{2}\) ta được thiết diện là một hình vuông. Tính thể tích khối trụ.
Gọi $\left( O \right)$ là một đường tròn đáy của hình trụ
Mặt phẳng đã cho cắt $\left( O \right)$ tại $A$ và $B$, gọi $H$ là trung điểm $AB$.
Vì thiết diện thu được là hình vuông nên chiều cao hình trụ bằng
$h = AB = 2AH = 2\sqrt {O{A^2} - O{H^2}} = a\sqrt 3 $
Thể tích khối trụ là
$V = \pi {R^2}h = \pi {a^2}.a\sqrt 3 = \pi {a^3}\sqrt 3 $
Hướng dẫn giải:
- Tính chiều cao hình trụ dựa vào định lý Pi-ta-go.
- Tính thể tích khối trụ dựa vào công thức \(V = \pi {R^2}h\)
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án B vì sau khi tính được \(AH = \dfrac{{a\sqrt 3 }}{2}\) thì tính ngay thể tích \(V = \dfrac{{\pi {a^3}\sqrt 3 }}{2}\) là sai.
Điều kiện để hàm số bậc ba không có cực trị là phương trình $y' = 0$ có:
Điều kiện để hàm số bậc ba không có cực trị là phương trình $y' = 0$ vô nghiệm hoặc có nghiệm kép.
Hướng dẫn giải:
Sử dụng điều kiện có cực trị của hàm số bậc ba:
Hàm số bậc ba không có cực trị nếu phương trình $y'=0$ vô nghiệm hoặc có nghiệm kép.
Gọi $m$ là giá trị nhỏ nhất của hàm số $y = x - 1 + \dfrac{4}{{x - 1}}$ trên khoảng $\left( {1; + \infty {\rm{\;}}} \right)$. Tìm $m?$
${\rm{\;}}x > 1 \Leftrightarrow x - 1 > 0$
$ \Rightarrow y = x - 1 + \dfrac{4}{{x - 1}} \ge 2\sqrt {\left( {x - 1} \right).\dfrac{4}{{x - 1}}} = 2.2 = 4$
Dấu bằng xảy ra $ \Leftrightarrow x - 1 = \dfrac{4}{{x - 1}} \Leftrightarrow {\left( {x - 1} \right)^2} = 4 \Leftrightarrow x = 3$.
Vậy GTNN của hàm số là $m=4$ khi $x=3$.
Hướng dẫn giải:
Sử dung BĐT Cauchy cho hai số không âm \(a + b \ge 2\sqrt {ab} \)
Giải thích thêm:
Các em cũng có thể đạo hàm và tìm GTNN như sau:
\(\begin{array}{l}y' = 1 - \frac{4}{{{{\left( {x - 1} \right)}^2}}}\\y' = 0 \Leftrightarrow 1 - \frac{4}{{{{\left( {x - 1} \right)}^2}}} = 0\\ \Leftrightarrow 1 = \frac{4}{{{{\left( {x - 1} \right)}^2}}} \Leftrightarrow {\left( {x - 1} \right)^2} = 4\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 2\\x - 1 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3 \in \left( {1; + \infty } \right)\\x = - 1 \notin \left( {1; + \infty } \right)\end{array} \right.\end{array}\)
Lập bảng biến thiên của hàm số trên \(\left( {1; + \infty } \right)\) ta thấy \({y_{\min }} = y\left( 3 \right) = 4\).
Cho hình lập phương \(ABCD.A'B'C'D'\) tâm \(O\). Phép dời hình nào không biến hình vuông \(ABCD\) thành hình vuông \(A'B'C'D'\)?
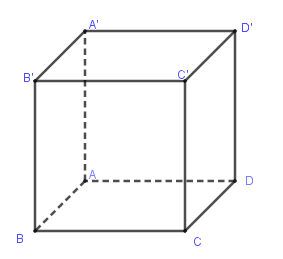
Dễ thấy, các phép tịnh tiến theo mỗi véc tơ \(\overrightarrow {AA'} ,\overrightarrow {BB'} ,\overrightarrow {CC'} ,\overrightarrow {DD'} \) biến hình vuông \(ABCD\) thành hình vuông \(A'B'C'D'\) nên B, C đúng, D sai.
Phép đối xứng qua tâm \(O\) của hình lập phương biến hình vuông \(ABCD\) thành hình vuông \(A'B'C'D'\) nên A đúng.
Hướng dẫn giải:
Nhận xét từng phép dời hình ở mỗi đáp án và kết luận.
Cho hàm số \(y = a{x^4} + b{x^2} + c\) có bảng biến thiên như hình vẽ. Chọn kết luận đúng:
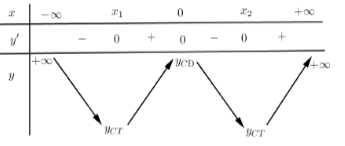
Từ bảng biến thiên ta thấy \(\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \) nên \(a > 0\).
Điều kiện để biểu thức ${a^\alpha }$ có nghĩa với $\alpha \in I$ là:
Lũy thừa với số mũ không nguyên thì cơ số phải dương nên $a > 0$.
Hướng dẫn giải:
Sử dụng chú ý về cơ số của các lũy thừa với số mũ nguyên, không nguyên:
+ Lũy thừa với số mũ nguyên dương thì không cần điều kiện cho cơ số.
+ Lũy thừa với số mũ nguyên âm và số mũ $0$ thì cơ số phải khác $0$.
+ Lũy thừa với số mũ không nguyên thì cơ số phải dương.
Cho hàm số \(y=\dfrac{2x+1}{x-2}\). Khẳng định nào dưới đây là đúng?
Xét hàm số \(y=\dfrac{2x+1}{x-2}\):
+) \(\mathop {\lim }\limits_{x \to {2^ + }} \dfrac{{2x + 1}}{{x - 2}} = + \infty ,\mathop {\lim }\limits_{x \to {2^ - }} \dfrac{{2x + 1}}{{x - 2}} = - \infty \)
Đồ thị hàm số có tiệm cận đứng là \(x=2\). Phương án A: đúng.
+) \(y'=-\dfrac{5}{{{(x-2)}^{2}}}<0,\,\,\forall x\ne 2\) \(\Rightarrow \) Hàm số \(y=\dfrac{2x+1}{x-2}\) không có cực trị và hàm số nghịch biến trên các khoảng \(\left( -\infty ;2 \right);\,\,\left( 2;+\infty \right)\). Phương án B và D: sai.
+) Ta có: \(3=\dfrac{2.1+1}{1-2}\) vô lí \(\Rightarrow \) Đồ thị hàm số không đi qua điểm\(A(1;3)\). Phương án C: sai.
Hướng dẫn giải:
- Tìm các tiệm cận đứng, ngang của đồ thị hàm số.
- Tìm các khoảng đồng biến nghịch biến của hàm số.
- Tìm các cực trị và xét tính đi qua một điểm của đồ thị hàm số.
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình vẽ:
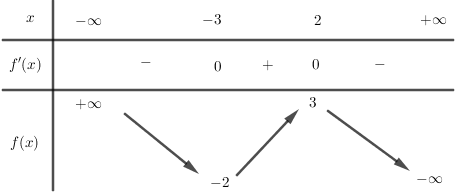
Trong các khẳng định sau, khẳng định nào đúng?
Nhận thấy hàm số nghịch biến trên các khoảng $\left( { - \infty ; - 3} \right)$ và $\left( {2; + \infty } \right)$
Hàm số có giá trị cực đại bằng 3 tại $x = 2$
Hướng dẫn giải:
Dựa vào bảng biến thiên và rút ra kết luận
Giải phương trình \({9^{\left| {x + 1} \right|}} = {27^{2x - 2}}.\) Ta có tập nghiệm bằng:
\(\begin{array}{l}{9^{\left| {x + 1} \right|}} = {27^{2x - 2}} \Leftrightarrow {3^{2\left| {x + 1} \right|}} = {3^{3\left( {2x - 2} \right)}} \Leftrightarrow 2\left| {x + 1} \right| = 6x - 6\\ \Leftrightarrow \left[ \begin{array}{l}2x + 2 = 6x - 6\,\,khi\,x \ge - 1\\2x + 2 = - 6x + 6\,\,khi\,x < - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\,\,\left( {tm} \right)\\x = \dfrac{1}{2}\,\,\left( {ktm} \right)\end{array} \right..\end{array}\)
Hướng dẫn giải:
Đưa về cùng cơ số 3.
Công thức tính thể tích khối nón biết diện tích đáy \({S_d}\) và đường sinh \(l\) là:
Ta có: \({l^2} = {r^2} + {h^2} \Rightarrow h = \sqrt {{l^2} - {r^2}} \Rightarrow V = \dfrac{1}{3}{S_d}.h = \dfrac{1}{3}{S_d}.\sqrt {{l^2} - {r^2}} \)
Hướng dẫn giải:
- Tính chiều cao \(h\) sử dụng công thức \({l^2} = {h^2} + {r^2}\)
- Tính thể tích khối nón \(V = \dfrac{1}{3}{S_d}.h\).
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án A vì nhớ nhầm công thức.
Phép vị tự tỉ số \(k > 0\) biến khối chóp có thể tích \(V\) thành khối chóp có thể tích \(V'\). Khi đó:
Phép vị tự tỉ số \(k > 0\) biến khối chóp có thể tích \(V\) thành khối chóp có thể tích \(V'\). Khi đó \(\dfrac{{V'}}{V} = {k^3}\).
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án C vì không nhớ kĩ công thức tính.
Chọn mệnh đề đúng:
Đáp án A: Vì \(\sqrt 3 > 1\) và \(\sqrt 3 > \sqrt 2 \) nên \({\left( {\sqrt 3 } \right)^{\sqrt 3 }} > {\left( {\sqrt 3 } \right)^{\sqrt 2 }}\) hay A đúng.
Đáp án B: Vì \(\dfrac{1}{{\sqrt 3 }} < 1\) và \(\sqrt 3 < \sqrt 5 \) nên \({\left( {\dfrac{1}{{\sqrt 3 }}} \right)^{\sqrt 3 }} > {\left( {\dfrac{1}{{\sqrt 3 }}} \right)^{\sqrt 5 }}\) hay B sai.
Đáp án C: \({\left( {\dfrac{1}{2}} \right)^{ - \sqrt 3 }} = {2^{\sqrt 3 }}\), \({\left( {\dfrac{1}{3}} \right)^{ - \sqrt 3 }} = {3^{\sqrt 3 }}\). Vì \(2 < 3\) nên \({2^{\sqrt 3 }} < {3^{\sqrt 3 }}\) hay \({\left( {\dfrac{1}{2}} \right)^{ - \sqrt 3 }} < {\left( {\dfrac{1}{3}} \right)^{ - \sqrt 3 }}\) nên C sai.
Đáp án D: Vì \(\dfrac{2}{3} > \dfrac{1}{3}\) nên \({\left( {\dfrac{2}{3}} \right)^{\sqrt 3 }} > {\left( {\dfrac{1}{3}} \right)^{\sqrt 3 }}\) hay D sai.
Hướng dẫn giải:
Sử dụng các tính chất so sánh lũy thừa:
- Với \(a > 1\) thì \({a^x} > {a^y} \Leftrightarrow x > y\); với \(0 < a < 1\) thì \({a^x} > {a^y} \Leftrightarrow x < y\).
- Với \(0 < a < b\) và \(m\) nguyên dương thì \({a^m} < {b^m}\); \(m\) nguyên âm thì \({a^m} > {b^m}\).
Hàm số $y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)$ có $1$ cực trị nếu và chỉ nếu:
Ta có: $y' = 4a{x^3} + 2bx = 2x\left( {2a{x^2} + b} \right)$.
Hàm số có $1$ cực trị $ \Leftrightarrow y' = 0$ có $1$ nghiệm duy nhất hay $y'=0$ vô nghiệm hoặc có nghiệm kép
\( \Leftrightarrow \left[ \begin{array}{l}ab > 0\\b \ge 0\end{array} \right. \Leftrightarrow ab \ge 0\)
Giải thích thêm:
HS thường nhầm lẫn khi xét phương trình $2a{x^2} + b = 0$ vô nghiệm thì chọn ngay $b > 0$ mà không để ý điều kiện của $a$ và chọn đáp án C là sai.
Tọa độ giao điểm của đường thẳng $d:y = 3x$ và parabol $\left( P \right):y = 2{x^2} + 1$ là:
Phương trình hoành độ $2{x^2} + 1 = 3x$.
$ \Leftrightarrow 2{x^2} - 3x + 1 = 0 \Leftrightarrow \left[ \begin{gathered} x = 1 \Rightarrow y = 3 \hfill \\ x = \dfrac{1}{2} \Rightarrow y = \dfrac{3}{2} \hfill \\ \end{gathered} \right.$
Vậy có hai giao điểm là $\left( {1;3} \right)$ và $\left( {\dfrac{1}{2};\dfrac{3}{2}} \right)$.
Hướng dẫn giải:
- Bước 1: Lập phương trình hoành độ giao điểm của đồ thị hàm số.
- Bước 2: Giải phương trình tìm $x$, rồi từ đó suy ra $y$ và tọa độ giao điểm.
Giải thích thêm:
HS thường nhẩm sai nghiệm của phương trình dẫn đến chọn sai đáp án D, hoặc một số em thử đáp án A hoặc B thấy thỏa mãn thì vội vàng chọn ngay A hoặc B là sai.
Đường cong hình bên là đồ thị hàm số nào sau đây:
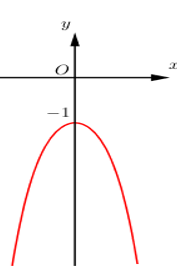
Dễ thấy $\mathop {\lim }\limits_{x \to + \infty } {\mkern 1mu} y = \mathop {\lim }\limits_{x \to - \infty } {\mkern 1mu} y = - \infty \Rightarrow a < 0 \Rightarrow $ Loại A và B.
Đồ thị hàm số đi qua $\left( {0; - 1} \right) \Rightarrow $ Loại C.
Hướng dẫn giải:
Dựa vào chiều của đồ thị hàm số tìm dấu của hệ số a.
Dựa vào các điểm mà đồ thị hàm số đi qua để loại các đáp án.
Trong các khẳng định sau, khẳng định nào đúng?
\(\log a + \log b = \log \left( {ab} \right)\) nên ý A sai
Nhận thấy \({a^{x + y}} = {a^x}.{a^y}\) nên mệnh đề ở ý B sai.
Vì $12 > 1$ nên \(y = {\log _{12}}x\) là hàm đồng biến trên khoảng $(0; + \infty )$ nên D sai
Hướng dẫn giải:
Sử dụng tính chất các hàm số mũ, logarit và các công thức biến đổi mũ, logarit.
Tập nghiệm của bất phương trình \({2^{{x^2} - 2x}} \le 8\):
\({2^{{x^2} - 2x}} \le 8 \Leftrightarrow {2^{{x^2} - 2x}} \le {2^3}\)
Vì \(2 > 1 \Rightarrow {x^2} - 2x \le 3 \Leftrightarrow {x^2} - 2x - 3 \le 0 \Leftrightarrow x \in \left[ { - 1;3} \right]\)
Hướng dẫn giải:
Sử dụng lý thuyết \({a^x} \le {a^y} \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}0 < a < 1\\x \ge y\end{array} \right.\\\left\{ \begin{array}{l}a > 1\\x \le y\end{array} \right.\end{array} \right.\)
Chọn khẳng định đúng:
Hàm số $y = \dfrac{1}{x}$ là hàm số lẻ nên đồ thị hàm số nhận điểm $\left( {0;0} \right)$ làm tâm đối xứng.
Hướng dẫn giải:
Sử dụng tính chất hàm số lẻ: Đồ thị hàm số lẻ luôn nhận điểm $\left( {0;0} \right)$ là tâm đối xứng.
Giải thích thêm:
Cần chú ý: Không có khái niệm tâm đối xứng của hàm số nên các đáp án C và D không cần xét tính đúng sai.
Tính thể tích \(V\) của khối trụ ngoại tiếp hình lập phương có cạnh bằng $a$.
Khối trụ ngoại tiếp hình lập phương có cạnh bằng $a$ thì bán kính đáy \(r = \dfrac{{a\sqrt 2 }}{2}\) và chiều cao \(h = a\).
Suy ra \(V = \pi {r^2}h = \dfrac{{\pi {a^3}}}{2}\)
Hướng dẫn giải:
Thể tích của khối trụ là:$V = \pi {R^2}h$.
Giải thích thêm:
Một số em sẽ tính nhầm bán kính \(r = \dfrac{{a\sqrt 3 }}{2}\) dẫn đến chọn nhầm đáp án A là sai.
Chọn mệnh đề sai:
Điểm không thuộc mặt cầu thì có thể nằm ngoài hoặc nằm trong mặt cầu nên các điểm nằm trong mặt cầu vẫn thuộc khối cầu.
Do đó \(C\) sai.
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án B vì không nhớ rõ định nghĩa điểm nằm ngoài mặt cầu.
Số mặt phẳng đối xứng của mặt cầu là:
Mọi mặt phẳng đi qua tâm của mặt cầu đều là mặt phẳng đối xứng của mặt cầu.
Vậy có vô số mặt phẳng đối xứng.
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình thang vuông tại \(A\) và \(D\) thỏa mãn \(SA \bot \left( {ABCD} \right)\) và \(AB = 2AD = 2CD = 2a = \sqrt 2 SA\). Thể tích khối chóp \(S.BCD\) là:
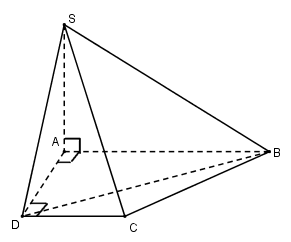
Ta có: \({S_{ABCD}} = \dfrac{1}{2}\left( {AB + CD} \right).AD = \dfrac{1}{2}\left( {2a + a} \right)a = \dfrac{{3{a^2}}}{2}\)
\({S_{\Delta ABD}} = \dfrac{1}{2}AD.AB = \dfrac{1}{2}a.2a = {a^2}\)
\( \Rightarrow {S_{BCD}} = {S_{ABCD}} - {S_{ABD}} = \dfrac{{3{a^2}}}{2} - {a^2} = \dfrac{{{a^2}}}{2}\)
\(SA = \dfrac{{2a}}{{\sqrt 2 }} = a\sqrt 2 \)
\( \Rightarrow {V_{S.BCD}} = \dfrac{1}{3}SA.{S_{BCD}} = \dfrac{1}{3}a\sqrt 2 .\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}\sqrt 2 }}{6}\)
Hướng dẫn giải:
- Bước 1: Tính diện tích đáy \({S_{\Delta BCD}}\), dựa vào các tính chất của đáy.
- Bước 2: Tính chiều cao \(h = SA\).
- Bước 3: Tính thể tích khối chóp \(V = \dfrac{1}{3}Sh\).
Giải thích thêm:
Một số em sẽ tính nhầm \(SA = \dfrac{{a\sqrt 2 }}{2}\) dẫn đến chọn nhầm đáp án D là sai.
Tìm số nghiệm nguyên của bất phương trình \({\left( {\dfrac{1}{3}} \right)^{\sqrt {{x^2} - 3x - 10} }} > {\left( {\dfrac{1}{3}} \right)^{x - 2}}\)
Vì $0 < \dfrac{1}{3} < 1$ nên ta có
\(\begin{array}{l}{\left( {\dfrac{1}{3}} \right)^{\sqrt {{x^2} - 3{\rm{x}} - 10} }} > {\left( {\dfrac{1}{3}} \right)^{x - 2}} \Leftrightarrow \sqrt {{x^2} - 3{\rm{x}} - 10} < x - 2 \\ \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 3{\rm{x}} - 10 < {\left( {x - 2} \right)^2}\\{x^2} - 3{\rm{x}} - 10 \ge 0\\x - 2 > 0\end{array} \right. \Leftrightarrow 5 \le x < 14\\ \Rightarrow x = \left\{ {5,6,7,8,9,10,11,12,13} \right\}\end{array}\)
Hướng dẫn giải:
Giải bất phương trình mũ:
$\begin{array}{l}{{\rm{a}}^{f\left( x \right)}} > {a^{g\left( x \right)}} \Leftrightarrow f(x) > g(x){\rm{ }}\left( {a > 1} \right)\\{{\rm{a}}^{f\left( x \right)}} < {a^{g\left( x \right)}} \Leftrightarrow f(x) > g(x){\rm{ }}\left( {0 < a < 1} \right)\end{array}$
Giải thích thêm:
Cần chú ý điều kiện \(0 < \dfrac{1}{3} < 1\), một số em không chú ý điều kiện này sẽ dẫn đến chọn nhầm đáp án A là sai.
Một số em khác lại quên không đặt điều kiện cho \(x\) để các biểu thức xác định, dẫn đến chỉ tìm ra \(x < 14\) và cũng chọn A, một số em thì bỏ quên điều kiện \(x > 2\) nên chỉ thu được \(x \le - 2\) hoặc \(5 \le x < 14\) và cũng chọn nhầm đáp án A là sai.
Diện tích xung quanh hình nón có bán kính đáy \(r = 3cm\) và độ dài đường sinh \(4cm\) là:
Áp dụng công thức \({S_{xq}} = \pi rl\) ta được: \({S_{xq}} = \pi .3.4 = 12\pi \left( {c{m^2}} \right)\)
Hướng dẫn giải:
Sử dụng công thức tính diện tích xung quanh \({S_{xq}} = \pi rl\).
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án B vì không đọc kỹ các đáp án.
Cho điểm \(A \in \left( P \right)\). Lấy đối xứng \(A\) qua \(\left( P \right)\) được ảnh là điểm \(A'\). Chọn kết luận đúng:
Phép đối xứng qua mặt phẳng \(\left( P \right)\) là phép biến hình biến mỗi điểm thuộc \(\left( P \right)\) thành chính nó nên \(A \equiv A'\).
Hướng dẫn giải:
Phép đối xứng qua mặt phẳng \(\left( P \right)\) là phép biến hình biến mỗi điểm thuộc \(\left( P \right)\) thành chính nó.
Mệnh đề nào sau đây là mệnh đề đúng ?
\(0<2-\sqrt{2}<1\Rightarrow {{\left( 2-\sqrt{2} \right)}^{3}}>{{\left( 2-\sqrt{2} \right)}^{4}}\Rightarrow \)Đáp án A sai.
\(4-\sqrt{2}>1\Rightarrow {{\left( 4-\sqrt{2} \right)}^{3}}<{{\left( 4-\sqrt{2} \right)}^{4}}\Rightarrow \)Đáp án B đúng.
\(\sqrt{11}-\sqrt{2}>1\Rightarrow {{\left( \sqrt{11}-\sqrt{2} \right)}^{6}}<{{\left( \sqrt{11}-\sqrt{2} \right)}^{7}}\Rightarrow \) Đáp án C sai.
\(0<\sqrt{3}-\sqrt{2}<1\Rightarrow {{\left( \sqrt{3}-\sqrt{2} \right)}^{4}}>{{\left( \sqrt{3}-\sqrt{2} \right)}^{5}}\Rightarrow \)Đáp án D sai.
Hướng dẫn giải:
\({a^x} < {a^y} \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a > 1\\x < y\end{array} \right.\\\left\{ \begin{array}{l}0 < a < 1\\x > y\end{array} \right.\end{array} \right.\)
Tập hợp tất cả các giá trị của m để hàm số $y = \dfrac{1}{3}{x^3} - \left( {m - 1} \right){x^2} + 2\left( {m - 1} \right)x - 2$ luôn tăng trên $R$
Xét hàm số: $y = \dfrac{1}{3}{x^3} - \left( {m - 1} \right){x^2} + 2\left( {m - 1} \right)x - 2$ trên $R$
Có $y'\left( x \right) = {x^2} - 2\left( {m - 2} \right)x + 2\left( {m - 1} \right).$
Hàm số đã cho tăng trên $R \Leftrightarrow y'\left( x \right) > 0,\forall x \in R$$ \Leftrightarrow \Delta ' = {\left( {m - 1} \right)^2} - 2\left( {m - 1} \right) \le 0$.
Vì $a = 1 > 0.$$ \Leftrightarrow {m^2} - 4m + 3 \le 0$$ \Leftrightarrow 1 \le m \le 3.$
Hướng dẫn giải:
Tính y' và tìm điều kiện của $m$ để $y' > 0,\forall x \in R$.
Điều kiện để tam thức bậc hai $a{x^2} + bx + c > 0,\forall x \in R$ là $\left\{ {\begin{array}{*{20}{l}}{a > 0}\\{\Delta {\rm{\;}} \le 0}\end{array}} \right.$
Số điểm cực trị của hàm số $y = {(x - 1)^{2017}}$ là
Tập xác định: $D = \mathbb{R}$
$y = {(x - 1)^{2017}} \Rightarrow y' = 2017{(x - 1)^{2016}} \ge 0,\forall x$
Do đó hàm số đồng biến trên $\mathbb{R}$ nên không có cực trị.
Hướng dẫn giải:
- Tính và tìm các nghiệm của $y' = 0$ và các điểm tại đó hàm số không xác định.
- Xét dấu y’ qua các điểm tìm được ở trên và kết luận:
Điểm làm cho đạo hàm đổi dấu là các điểm cực trị của hàm số.
Cho hàm số $y = {x^3} - 3m{x^2} + 6$, giá trị nhỏ nhất của hàm số trên $\left[ {0;3} \right]$ bằng $2$ khi:
TXĐ: $D = \mathbb{R}$
$y' = 3{x^2} - 6mx.$
Ta có: $y' = 0 \Leftrightarrow \left[ \begin{gathered}x = 0 \Rightarrow y = 6 \hfill \\x = 2m \Rightarrow y = - 4{m^3} + 6 \hfill \\ \end{gathered} \right.$
$y^{\prime}=0 \Leftrightarrow\left[\begin{array}{c}x=0 \Rightarrow y=6 \\ x=2 m \Rightarrow y=-4 m^{3}+6\end{array}\right.$
Xét TH1: $m = 0$. Hàm số đồng biến trên $\left[ {0;3} \right]$ $ \Rightarrow \mathop {Min}\limits_{\left[ {0;3} \right]} y = y\left( 0 \right) = 6 \Rightarrow $ loại.
Xét TH2: $m \geqslant \dfrac{3}{2} \Rightarrow 2m \ge 3 > 0$. Khi đó, hàm số nghịch biến trên $\left[ {0;3} \right] \subset \left[ {0;2m} \right]$
$ \Rightarrow \mathop {Min}\limits_{\left[ {0;3} \right]} y = y\left( 3 \right) = 33 - 27m = 2 \Rightarrow m = \dfrac{{31}}{{27}} < \dfrac{3}{2}$(loại)
Xét TH3: $\dfrac{3}{2} > m > 0 \Rightarrow 3 > 2m > 0$ thì đồ thị hàm số có điểm cực đại là $\left( {0;6} \right)$ và điểm cực tiểu là $\left( {2m, - 4{m^3} + 6} \right).$
Khi đó , GTNN trên $\left[ {0;3} \right]$ là $y\left( {2m} \right) = - 4{m^3} + 6$ $ \Rightarrow - 4{m^3} + 6 = 2 \Leftrightarrow {m^3} = 1 \Leftrightarrow m = 1$ (thỏa mãn)
Xét TH4: $m < 0 \Rightarrow \left( {0;6} \right)$ là điểm cực tiểu của đồ thị hàm số và trên $\left[ {0;3} \right]$ hàm số đồng biến.
$ \Rightarrow {y_{min}} = 6 \Rightarrow $ loại.
Vậy $m = 1$ là giá trị cần tìm.
Hướng dẫn giải:
- Tính $y'$ và tìm nghiệm của $y' = 0$.
- Biện luận các trường hợp điểm $x = 3$ nằm trong, nằm ngoài khoảng 2 nghiệm để suy ra kết luận.
Các TH cần xét:
1) $m=0$
2) $m>0$ ta có $0<2m$ nên chia thành 2 TH nhỏ: $0<2m<3$ và $0<3 \le 2m$
3) $m<0$ ta có $2m<0 $ nên ta có luôn $2m<0<3$
Giải thích thêm:
HS cần phải xét tất cả các trường hợp và chú ý loại nghiệm. nhiều em sai lầm kết luận $m = \dfrac{{31}}{{27}}$ mà không chú ý điều kiện của trường hợp đó là $m \geqslant \dfrac{3}{2}$.
Cho hàm số $y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)$ có $1$ cực trị. Khi đó, nếu đồ thị hàm số nằm hoàn toàn phía trên trục hoành (không có điểm chung với trục hoành) thì:
Hàm số chỉ có 1 cực trị thì $y' = 0$ có 1 nghiệm $ \Leftrightarrow ab \ge 0$, khi đó đồ thị có dạng:
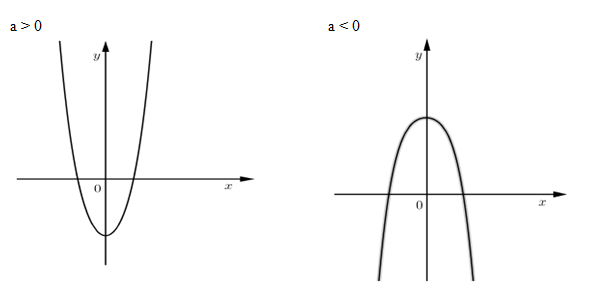
Trong hai trường hợp trên ta thấy nếu đồ thị hàm số nằm hoàn toàn phía trên trục hoành thì chỉ xảy ra trường hợp $a > 0$, do đó $b \ge 0$ và điểm cực tiểu $\left( {0;c} \right)$ cũng phải nằm phía trên trục hoành hay $c > 0$.
Hướng dẫn giải:
Vẽ các dạng đồ thị hàm số bậc bốn trùng phương có 1 cực trị và kết hợp với điều kiện bài cho để tìm ra đáp án đúng.
Giải thích thêm:
Nhiều HS đọc không kỹ đề sẽ chọn nhầm đáp án C, hoặc một số em khác nhầm lẫn với trường hợp hàm số có 3 cực trị và chọn nhầm đáp án B.
Hàm số nào sau đây có đồ thị như hình vẽ?
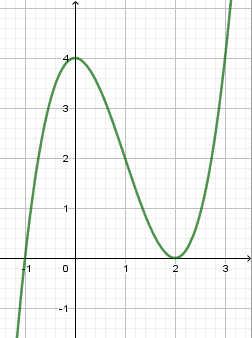
Đồ thị hàm số đi qua điểm $\left( {0;4} \right)$ nên loại A và D
Đồ thị hàm số cắt $Ox$ tại điểm $\left( { - 1;0} \right)$ và tiếp xúc $Ox$ tại $\left( {2;0} \right)$ nên phương trình hoành độ giao điểm $y = 0$ có 1 nghiệm đơn $x=-1$ và 1 nghiệm kép ${x_{2,3}} = 2$
Vậy chỉ có đáp án B thỏa mãn.
Hướng dẫn giải:
Quan sát đồ thị và nhận xét điểm cực đại, cực tiểu, điểm đi qua,… từ đó rút ra kết luận.
Đồ thị hàm số $y = \dfrac{{ax + 2}}{{2x + d}}$ như hình vẽ bên.
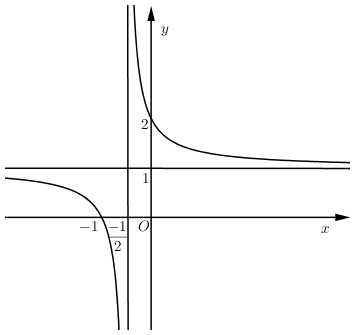
Chọn khẳng định đúng:
Đồ thị hàm số $y = \dfrac{{ax + 2}}{{2x + d}}$ có $\left\{ \begin{align} & \xrightarrow{TCD}x=-\dfrac{d}{2}=-\dfrac{1}{2}\Rightarrow d=1 \\ & \xrightarrow{TCN}y=\dfrac{a}{2}=1\Rightarrow a=2 \\ \end{align} \right.\Rightarrow 3a+d=7$
Hướng dẫn giải:
- Quan sát bảng biến thiên, tìm các đường tiệm cận đứng, ngang của đồ thị hàm số.
- Tìm $a,d$ và thay vào kiểm tra các đáp án.
Giải thích thêm:
Sau khi tìm xong $a,d$ thì HS thường tính sai giá trị các biểu thức bài cho dẫn đến chọn nhầm đáp án A là sai.
Hàm số $y = \dfrac{{bx - c}}{{x - a}}$ $\left( {a \ne 0;} \right.$ $\left. {a,{\rm{ }}b,{\rm{ }}c \in \mathbb{R}} \right)$ có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng?
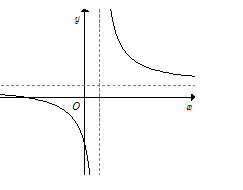
Đồ thị hàm số có tiệm cận đứng $x = a > 0$; tiệm cận ngang \(y = b > 0.\)
Mặt khác, ta thấy dạng đồ thị là đường cong đi xuống từ trái sang phải trên các khoảng xác định của nó nên
Vậy \(a > 0,{\rm{ }}b > 0,{\rm{ }}c - ab < 0.\)
Hướng dẫn giải:
Tìm các đường tiệm cận của đồ thị hàm số, nhận xét tính đồng biến, nghịch biến rồi suy ra mối quan hệ giữa các hệ số \(a,b,c\)
Tìm $m$ để phương trình ${x^5} + {x^3} - \sqrt {1 - x} + m = 0$ có nghiệm trên $\left( { - \infty ;1} \right]$.
Ta có số nghiệm của phương trình đã cho là số giao điểm của đồ thị (C): $y = {x^5} + {x^3} - \sqrt {1 - x} $ và đường thẳng d: $y = - m$.
Xét hàm số (C): $y = {x^5} + {x^3} - \sqrt {1 - x} $ có: $y' = 5{x^4} + 3{x^2} + \dfrac{1}{{2\sqrt {1 - x} }} > 0\,\,\forall x \in \left( { - \infty ;1} \right)$$ \Rightarrow $ hàm số luôn đồng biến trên $\left( { - \infty ;1} \right]$.
Lại có $y\left( 1 \right) = 2$.
Ta có BBT:
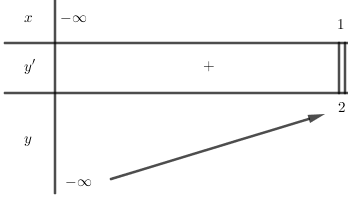
Theo BBT ta thấy pt có nghiệm $ \Leftrightarrow - m \leqslant 2 \Leftrightarrow m \geqslant - 2$.
Hướng dẫn giải:
- Nêu mối quan hệ giữa số nghiệm của phương trình và số giao điểm của $d$ và $\left( C \right)$.
- Khảo sát hàm số $y = {x^5} + {x^3} - \sqrt {1 - x} $ trên $\left( { - \infty ;1} \right]$ và từ đó suy ra điều kiện của $m$.
Đơn giản biểu thức $P = \left( {{a^{\dfrac{1}{4}}} - {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{4}}} + {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{2}}} + {b^{\dfrac{1}{2}}}} \right)\,\,\,\,(a,b > 0)$ ta được:
Ta có:
$P = \left( {{a^{\dfrac{1}{4}}} - {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{4}}} + {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{2}}} + {b^{\dfrac{1}{2}}}} \right) = \left( {{a^{\dfrac{1}{2}}} - {b^{\dfrac{1}{2}}}} \right)\left( {{a^{\dfrac{1}{2}}} + {b^{\dfrac{1}{2}}}} \right) = a - b$
Vậy \(P = a - b\).
Hướng dẫn giải:
Sử dụng các công thức lũy thừa với số mũ hữu tỉ \({a^m}.{a^n} = {a^{m + n}}\).
Giải thích thêm:
HS cần chú ý, tránh sử dụng nhầm công thức \({a^m}.{a^n} = {a^{mn}}\) sẽ dẫn đến chọn nhầm đáp án .
Các em cũng có thể thực hiện phép nhân bằng việc sử dụng hằng đẳng thức $a^2-b^2=(a-b)(a+b)$
Rút gọn biểu thức $B = \dfrac{{{a^{2\sqrt 2 }} - {b^{2\sqrt 3 }}}}{{{{\left( {{a^{\sqrt 2 }} - {b^{\sqrt 3 }}} \right)}^2}}} + 1$ ta được kết quả là:
Ta có: $B = \dfrac{{{a^{2\sqrt 2 }} - {b^{2\sqrt 3 }}}}{{{{\left( {{a^{\sqrt 2 }} - {b^{\sqrt 3 }}} \right)}^2}}} + 1 = \dfrac{{\left( {{a^{\sqrt 2 }} - {b^{\sqrt 3 }}} \right)\left( {{a^{\sqrt 2 }} + {b^{\sqrt 3 }}} \right)}}{{{{\left( {{a^{\sqrt 2 }} - {b^{\sqrt 3 }}} \right)}^2}}} + 1 $
$= \dfrac{{{a^{\sqrt 2 }} + {b^{\sqrt 3 }}}}{{{a^{\sqrt 2 }} - {b^{\sqrt 3 }}}} + 1 = \dfrac{{{a^{\sqrt 2 }} + {b^{\sqrt 3 }} + {a^{\sqrt 2 }} - {b^{\sqrt 3 }}}}{{{a^{\sqrt 2 }} - {b^{\sqrt 3 }}}} = \dfrac{{2{a^{\sqrt 2 }}}}{{{a^{\sqrt 2 }} - {b^{\sqrt 3 }}}}$
Hướng dẫn giải:
Sử dụng công thức ${a^{xy}} = {\left( {{a^x}} \right)^y}$ kết hợp sử dụng hằng đẳng thức, quy đồng mẫu thức để biến đổi và rút gọn $B$.
Giải thích thêm:
Ở bước quy đồng nhiều em HS sẽ tính nhầm tử thức ${a^{\sqrt 2 }} + {b^{\sqrt 3 }} + {a^{\sqrt 2 }} - {b^{\sqrt 3 }} = 0$ dẫn đến chọn nhầm đáp án D là sai.
Một khu rừng ở tỉnh Hà Giang có trữ lượng gỗ là $3.10^5(m^3).$ Biết tốc độ sinh trưởng của các ở khu rừng đó là $5\%$ mỗi năm. Hỏi sau $5$ năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ?
Trữ lượng gỗ sau năm thứ nhất: ${3.10}^5.(1+0,05)$
Trữ lượng gỗ sau năm thứ 2: ${3.10}^5.(1+0,05).+{3.10}^5.(1+0,05).0,05={3.10}^5.{(1+0,05)}^2$
Tương tự như vậy đến năm thứ 5 trữ lượng gỗ ở khu rừng đó là : ${3.10}^5.{(1+0,05)}^5$
Hướng dẫn giải:
Sử dụng công thức lãi kép $T = A{\left( {1 + r} \right)^N}$
Đặt \(a = {\log _3}4,b = {\log _5}4\) . Hãy biểu diễn \({\log _{12}}80\) theo $a$ và $b$
Ta có $80 = {4^2}.5;{\rm{ }}12 = 3.4$
$\begin{array}{l}{\log _{12}}80 = {\log _{12}}{4^2} + {\log _{12}}5 = 2{\log _{12}}4 + {\log _{12}}5 = \dfrac{2}{{{{\log }_4}12}} + \dfrac{1}{{{{\log }_5}12}} = \dfrac{2}{{{{\log }_4}3 + 1}} + \dfrac{1}{{{{\log }_5}3 + {{\log }_5}4}}\\ = \dfrac{2}{{\dfrac{1}{a} + 1}} + \dfrac{1}{{\dfrac{b}{a} + b}} = \dfrac{{2a}}{{a + 1}} + \dfrac{a}{{b\left( {a + 1} \right)}} = \dfrac{{2ab + a}}{{ab + b}}\end{array}$
Hướng dẫn giải:
Công thức đổi cơ số ${\log _a}b = \dfrac{{{{\log }_c}b}}{{{{\log }_c}a}}$; ${\log _a}b = \dfrac{1}{{{{\log }_b}a}};{\rm{ }}{\log _a}bc = {\log _a}b + {\log _a}c$
Trong các khẳng định dưới đây, khẳng định nào sai?
${\log _{0.5}}a > {\log _{0.5}}b \Leftrightarrow a < b{\rm{ }}$ vì $0,5 <1$ suy ra A sai.
$\log x < 0 \Leftrightarrow \log x < \log 1 \Leftrightarrow 0 < x < 1$ suy ra B đúng.
${\log _2}x > 0 \Leftrightarrow {\log _2}x > {\log _2}1 \Leftrightarrow x > 1$ suy ra C đúng.
${\log _{\dfrac{1}{3}}}a = {\log _{\dfrac{1}{3}}}b \Leftrightarrow a = b > 0{\rm{ }}$suy ra D đúng.
Hướng dẫn giải:
Ta có
$\begin{array}{l}{\log _a}b > {\log _a}c \Leftrightarrow b > c{\rm{ }}\left( {a > 1} \right)\\{\log _a}b > {\log _a}c \Leftrightarrow b < c{\rm{ }}\left( {0 < a < 1} \right)\end{array}$
Tìm $m$ để phương trình \({4^x} - {\text{ }}{2^{x{\text{ }} + {\text{ }}3}} + {\text{ }}3{\text{ }} = {\text{ }}m\) có đúng 2 nghiệm $x \in \left( {1;3} \right)$ .
Đặt $t = {2^x};x \in \left( {1;3} \right) \Rightarrow t = {2^x} \in \left( {2;8} \right)$
Xét hàm số \(y = {t^2} - 8t + 3\) trên \((2;8)\) có:
$y' = 2t - 8;$ $y' = 0 \Leftrightarrow 2t - 8 = 0 \Leftrightarrow t = 4\in (2;8)$
Bảng biến thiên:
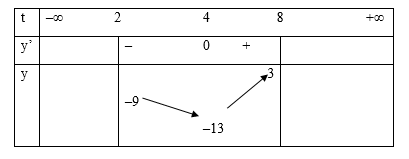
Căn cứ bảng biến thiên:
Phương trình \({4^x} - {\text{ }}{2^{x{\text{ }} + {\text{ }}3}} + {\text{ }}3{\text{ }} = {\text{ }}m\) có đúng 2 nghiệm \(x \in \left( {1;3} \right) \Leftrightarrow - 13 < m < - 9\)
Hướng dẫn giải:
- Đặt ẩn phụ đưa phương trình về bậc hai.
- Tìm điều kiện để bài toán phụ có nghiệm thỏa mãn điều kiện của ẩn phụ,
Cho hàm số \(y = f\left( x \right) = {2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018\) có đồ thị cắt trục hoành tại ba điểm phân biệt có hoành độ \({x_1};{x_2};{x_3}\). Tính giá trị biểu thức \(P = \dfrac{1}{{f'\left( {{x_1}} \right)}} + \dfrac{1}{{f'\left( {{x_2}} \right)}} + \dfrac{1}{{f'\left( {{x_3}} \right)}}.\)
Ta có \(f\left( x \right) = {2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018\)
\( \Rightarrow f'\left( x \right) = {3.2^{2019}}{x^2} + {3.2^{2019}}x = {3.2^{2019}}x\left( {x + 1} \right)\) \( \Rightarrow \dfrac{1}{{f'\left( x \right)}} = \dfrac{1}{{{{3.2}^{2019}}}}.\dfrac{1}{{x.\left( {x + 1} \right)}} = \dfrac{1}{{{{3.2}^{2019}}}}\left( {\dfrac{1}{x} - \dfrac{1}{{x + 1}}} \right)\)
Xét phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành \({2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018 = 0\) (*)
Vì \({x_1},{x_2},{x_3}\) là ba ngiệm của phương trình (*) nên theo hẹ thức Vi-et ta có
\(\left\{ \begin{array}{l}{x_1} + {x_2} + {x_3} = \dfrac{{ - 3}}{2}\\{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3} = 0\\{x_1}{x_2}{x_3} = \dfrac{{2018}}{{{2^{2019}}}}\end{array} \right.\)
Ta có \(P = \dfrac{1}{{f'\left( {{x_1}} \right)}} + \dfrac{1}{{f'\left( {{x_2}} \right)}} + \dfrac{1}{{f'\left( {{x_3}} \right)}} = \dfrac{1}{{{{3.2}^{2019}}}}\left( {\dfrac{1}{{{x_1}}} - \dfrac{1}{{{x_1} + 1}} + \dfrac{1}{{{x_2}}} - \dfrac{1}{{{x_2} + 1}} + \dfrac{1}{{{x_3}}} - \dfrac{1}{{{x_3} + 1}}} \right)\)
\( = \dfrac{1}{{{{3.2}^{2019}}}}\left[ {\left( {\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} + \dfrac{1}{{{x_3}}}} \right) - \left( {\dfrac{1}{{{x_1} + 1}} + \dfrac{1}{{{x_2} + 1}} + \dfrac{1}{{{x_3} + 1}}} \right)} \right]\)
\( = \dfrac{1}{{{{3.2}^{2019}}}}\left[ {\dfrac{{{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3}}}{{{x_1}{x_2}{x_3}}} - \dfrac{{\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right) + \left( {{x_1} + 1} \right)\left( {{x_3} + 1} \right) + \left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right)}}} \right]\)
\( = \dfrac{1}{{{{3.2}^{2019}}}}\left( {0 - \dfrac{{{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3} + 2\left( {{x_1} + {x_2} + {x_3}} \right) + 3}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right)}}} \right)\)
\( = \dfrac{1}{{{{3.2}^{2019}}}}.\dfrac{{0 + 2.\dfrac{{ - 3}}{2} + 3}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right)}} = 0\)
Hướng dẫn giải:
Sử dụng hệ thức Vi-et cho phương trình bậc ba \(a{x^3} + b{x^2} + cx + d = 0\,\left( {a \ne 0} \right)\) có ba nghiệm \({x_1},{x_2},{x_3}\)
\(\left\{ \begin{array}{l}{x_1} + {x_2} + {x_3} = \dfrac{{ - b}}{a}\\{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3} = \dfrac{c}{a}\\{x_1}{x_2}{x_3} = - \dfrac{d}{a}\end{array} \right.\)
Sau đó biến đổi \(f'\left( x \right)\) để tính \(P.\)
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\) có bảng biến thiên như sau:
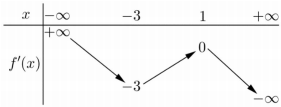
Bất phương trình \(f\left( x \right) < {e^x} + m\) đúng với mọi \(x \in \left( { - 1;1} \right)\) khi và chỉ khi:
Theo đề bài ta có : \(f\left( x \right) < {e^x} + m \Leftrightarrow f\left( x \right) - {e^x} < m\)
Đặt \(g\left( x \right) = f\left( x \right) - {e^x}.\) Khi đó :
\(\begin{array}{l}f\left( x \right) < {e^x} + m\,\,\forall x \in \left( { - 1;1} \right)\\ \Rightarrow g\left( x \right) = f\left( x \right) - {e^x} < m\,\,\forall x \in \left( { - 1;1} \right)\\ \Leftrightarrow m \ge \mathop {\max }\limits_{\left[ { - 1;1} \right]} g\left( x \right)\\g'\left( x \right) = f'\left( x \right) - {e^x}\end{array}\)
Trên \(\left( { - 1;1} \right)\) ta có \(f'\left( x \right) < 0;\,\,{e^x} > 0\,\,\forall x \in R \Rightarrow g'\left( x \right) < 0\,\,\forall x \in \left( { - 1;1} \right)\)
\( \Rightarrow g\left( x \right)\) nghịch biến trên \(\left( { - 1;\;1} \right).\)
\(\begin{array}{l} \Rightarrow \mathop {\max }\limits_{\left[ { - 1;1} \right]} g\left( x \right) = g\left( { - 1} \right) = f\left( { - 1} \right) - {e^{ - 1}} = f\left( { - 1} \right) - \dfrac{1}{e}\\ \Rightarrow m \ge f\left( { - 1} \right) - \dfrac{1}{e}.\end{array}\)
Hướng dẫn giải:
Cô lập m, đưa bất phương trình về dạng \(g\left( x \right) < m\,\,\forall x \in \left( {a;b} \right) \Leftrightarrow m \ge \mathop {\max }\limits_{\left[ {a;b} \right]} g\left( x \right)\).
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e,\) với \(a,b,c,d,e \in \mathbb{R}.\) Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?
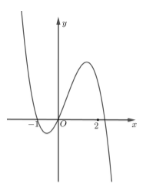
Ta có \(f'\left( x \right) = 4a{x^3} + 3b{x^2} + 2cx + d\)
Từ đồ thị hàm số ta thấy \(f'\left( 0 \right) \Leftrightarrow d = 0\)
Từ đồ thị ta thấy:
+ Khi $x< -1$ thì $f'(x)>0$.
+ Khi $-1<x<0=>f'(x)<0$
+ Khi $0<x<x_0$ (với $x_0$ là nghiệm thứ 3 của phương trình $f'(x)=0$) $=>f'(x)>0$
+ Khi $x>x_0$ thì $f'(x)<0$
Ta có bảng biến thiên:
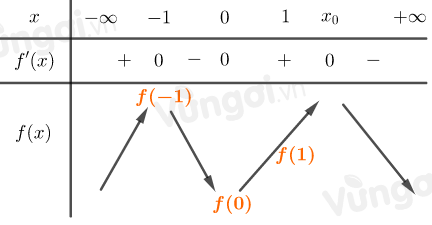
\(\Rightarrow f\left( { - 1} \right) > f\left( 0 \right)\)
\( \Leftrightarrow a - b + c - d + e > e \Leftrightarrow a + c > b + d\) nên B sai, lại có \(d = 0 \Rightarrow a + c > b\) (1)
+) Từ bảng biến thiên \( \Rightarrow f\left( 1 \right) > f\left( 0 \right)\)
\( \Leftrightarrow a + b + c + d + e > e \Leftrightarrow a + b + c + d > 0\) nên A sai.
Mà \(d = 0\) nên \(a + b + c > 0 \Leftrightarrow a + c > - b\) (2)
Từ (1) và (2) suy ra \(2\left( {a + c} \right) > 0 \Leftrightarrow a + c > 0.\)
Hướng dẫn giải:
Từ đồ thị hàm số suy ra \(f'\left( 0 \right) = 0;\,f'\left( x \right) > 0,\forall x \in \left( {0;1} \right)\)
Lập bảng biến thiên của hàm số $y=f(x)$
Cho $x, y$ là các số thực thỏa mãn \({\log _4}\left( {x + y} \right) + {\log _4}\left( {x - y} \right) \ge 1\). Tìm giá trị nhỏ nhất \({P_{\min }}\) của biểu thức \(P = 2x - y\).
Điều kiện : $x + y >0, x – y > 0$
\({\log _4}\left( {x + y} \right) + {\log _4}\left( {x - y} \right) \ge 1 \Leftrightarrow {\log _4}\left( {{x^2} - {y^2}} \right) \ge 1 \Leftrightarrow {x^2} - {y^2} \ge 4\)
Ta có: $P = 2x - y = \dfrac{{x + y + 3(x - y)}}{2} \ge \sqrt {(x + y).3(x - y)} = \sqrt {3({x^2} - {y^2})} = \sqrt {3.4} = 2\sqrt 3 $
Dấu “=” xảy ra khi:
\(\left\{ \begin{array}{l}x + y = 3\left( {x - y} \right)\\{x^2} - {y^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y = 3\left( {x - y} \right)\\3{\left( {x - y} \right)^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - y = \dfrac{2}{{\sqrt 3 }}\\x + y = 2\sqrt 3 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{{\sqrt 3 }} + \sqrt 3 \\y = \sqrt 3 - \dfrac{1}{{\sqrt 3 }}\end{array} \right.\)
Vậy $Min\,P = 2\sqrt 3 $.
Hướng dẫn giải:
Sử dụng bất đẳng thức Cô si: $\forall x,y \ge 0$ ta có: $\dfrac{{x + y}}{2} \ge \sqrt {xy} $
Cho phương trình \({x^3} + \left( {m - 12} \right)\sqrt {4x - m} = 4x\left( {\sqrt {4x - m} - 3} \right)\), với \(m\) là tham số. Có bao nhiêu giá trị nguyên của m để phương trình đã cho có hai nghiệm thực phân biệt?
ĐKXĐ: \(x \ge \dfrac{m}{4}\)
Ta có: \({x^3} + \left( {m - 12} \right)\sqrt {4x - m} = 4x\left( {\sqrt {4x - m} - 3} \right)\\ \Leftrightarrow {x^3} + 12x = \left( {4x - m} \right)\sqrt {4x - m} + 12\sqrt {4x - m} \)
\( \Leftrightarrow {x^3} + 12x = {\left( {\sqrt {4x - m} } \right)^3} + 12\sqrt {4x - m} (*)\)
Xét hàm số \(f\left( t \right) = {t^3} + 12t,\,\,\,f'\left( t \right) = 3{t^2} + 12 > 0,\,\forall t \Rightarrow \) Hàm số đồng biến trên \(\mathbb{R}\)
Phương trình (*) trở thành
\( f\left( x \right) = f\left( {\sqrt {4x - m} } \right)\)
\( \Leftrightarrow x = \sqrt {4x - m} \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\{x^2} = 4x - m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\m = 4x - {x^2} = g\left( x \right)\end{array} \right.\)

Phương trình đã cho có hai nghiệm thực phân biệt \( \Leftrightarrow 0 \le m < 4 \Rightarrow m \in \left\{ {0;1;2;3} \right\}\): 4 giá trị thỏa mãn.
Hướng dẫn giải:
Sử dụng phương pháp xét tính đơn điệu của hàm số.
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng \(a\). Biết tam giác \(SBA\) vuông tại \(B\), tam giác \(SCA\) vuông tại \(C\) và khoảng cách giữa hai đường thẳng \(AC\) và \(SB\) bằng \(\dfrac{{3a}}{{\sqrt {13} }}\). Tính thể tích khối chóp \(S.ABC\).
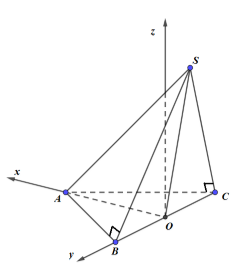
Gọi O là trung điểm của BC.
Ta gắn hệ trục tọa độ Oxyz như hình vẽ. Trong đó:
\(A\left( {\dfrac{{a\sqrt 3 }}{2};0;0} \right),\,B\left( {0;\dfrac{a}{2};0} \right),\,C\left( {0; - \dfrac{a}{2};0} \right)\)
Gọi \(\left( P \right)\) là mặt phẳng vuông góc với AB tại B, \(\left( Q \right)\) là mặt phẳng vuông góc với AC tại C. Gọi giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\) là đường thẳng \(d\).
Do \(SB \bot AB,\,\,SC \bot AC\) nên \(S \in d\).
\(\overrightarrow {AB} = \left( { - \dfrac{{a\sqrt 3 }}{2};\dfrac{a}{2};0} \right),\,\,\overrightarrow {AC} = \left( { - \dfrac{{a\sqrt 3 }}{2}; - \dfrac{a}{2};0} \right)\)
Mặt phẳng \(\left( P \right)\) đi qua \(B\left( {0;\dfrac{a}{2};0} \right)\), nhận \(\overrightarrow {{n_1}} = \left( {\sqrt 3 ; - 1;0} \right)\) là 1 VTPT, có phương trình là: \(\sqrt 3 x - y + \dfrac{a}{2} = 0\).
Mặt phẳng \(\left( Q \right)\) đi qua \(C\left( {0; - \dfrac{a}{2};0} \right)\), nhận \(\overrightarrow {{n_2}} = \left( {\sqrt 3 ;1;0} \right)\) là 1 VTPT, có phương trình là: \(\sqrt 3 x + y + \dfrac{a}{2} = 0\).
\(d\) là giao của \(\left( P \right)\) và \(\left( Q \right) \Rightarrow d:\left\{ \begin{array}{l}\sqrt 3 x - y + \dfrac{a}{2} = 0\\\sqrt 3 x + y + \dfrac{a}{2} = 0\end{array} \right.\), \(\left[ {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right] = \left( {0;0;2\sqrt 3 } \right)\)
\( \Rightarrow d\) đi qua \(I\left( { - \dfrac{a}{{2\sqrt 3 }};0;0} \right)\)có 1 VTCP \(\overrightarrow u = \left( {0;0;1} \right)\), có phương trình tham số là: \(\left\{ \begin{array}{l}x = - \dfrac{a}{{2\sqrt 3 }}\\y = 0\\z = t\end{array} \right.\)
Giả sử \(S\left( { - \dfrac{a}{{2\sqrt 3 }};0;t} \right)\). Ta có: \(\begin{array}{l}\overrightarrow {SB} = \left( {\dfrac{a}{{2\sqrt 3 }};\dfrac{a}{2}; - t} \right);\,\,\\\overrightarrow {CA} = \left( {\dfrac{{a\sqrt 3 }}{2};\dfrac{a}{2};0} \right)\end{array}\)\( \Rightarrow \left[ {\overrightarrow {SB} ;\overrightarrow {CA} } \right] = \left( {\dfrac{{at}}{2};\dfrac{{a\sqrt 3 t}}{2}; - \dfrac{{{a^2}\sqrt 3 }}{6}} \right)\)\( \Rightarrow \left| {\left[ {\overrightarrow {SB} ;\overrightarrow {CA} } \right]} \right| = \sqrt {\dfrac{{{a^2}{t^2}}}{4} + \dfrac{{3{a^2}{t^2}}}{4} + \dfrac{{{a^2}}}{{12}}} = \sqrt {{a^2}{t^2} + \dfrac{{{a^2}}}{{12}}} \)
Ta có: \(\overrightarrow {CB} = \left( {0;a;0} \right)\)\( \Rightarrow \left[ {\overrightarrow {SB} ;\overrightarrow {CA} } \right].\overrightarrow {CB} = 0 + \dfrac{{a\sqrt 3 t}}{2}.a + 0 = \dfrac{{{a^2}\sqrt 3 t}}{2}\)
\(d(SB;AC) = \dfrac{{\left| {\left[ {\overrightarrow {SB} ;\overrightarrow {CA} } \right].\overrightarrow {CB} } \right|}}{{\left| {\left[ {\overrightarrow {SB} ;\overrightarrow {CA} } \right]} \right|}} = \dfrac{{\left| {\dfrac{{{a^2}\sqrt 3 t}}{2}} \right|}}{{\sqrt {{a^2}{t^2} + \dfrac{{{a^2}}}{{12}}} }}\)
\(\begin{array}{l} \Rightarrow \dfrac{{\left| {\dfrac{{{a^2}\sqrt 3 t}}{2}} \right|}}{{\sqrt {{a^2}{t^2} + \dfrac{{{a^2}}}{{12}}} }} = \dfrac{{3a}}{{\sqrt {13} }} \Leftrightarrow \dfrac{{3{a^4}{t^2}}}{{4{a^2}{t^2} + \dfrac{1}{3}{a^2}}} = \dfrac{{9{a^2}}}{{13}}\\ \Leftrightarrow 39{a^2}{t^2} = 36{a^2}{t^2} + 3{a^2} \Leftrightarrow {t^2} = {a^2} \Leftrightarrow t = a\end{array}\)
\( \Rightarrow S\left( { - \dfrac{a}{{2\sqrt 3 }};0;a} \right)\)\( \Rightarrow h = d\left( {S;\left( {Oxy} \right)} \right) = a\)
Diện tích tam giác đều ABC là: \(S = \dfrac{{{a^2}\sqrt 3 }}{4}\)\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}.h.S = \dfrac{1}{3}.a.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{12}}\).
Hướng dẫn giải:
Gắn hệ trục tọa độ.
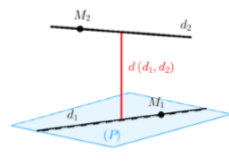
Đường thẳng \({d_1}\) có 1 VTCP \(\overrightarrow {{u_1}} \), đi qua điểm \({M_1}\).
Đường thẳng \({d_2}\) có 1 VTCP \(\overrightarrow {{u_2}} \), đi qua điểm \({M_2}\).
Khoảng cách giữa \({d_1}\) và \({d_2}\) được tính theo công thức:
\(d({d_1};{d_2}) = \dfrac{{\left| {\overrightarrow {{M_1}{M_2}} .\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right]} \right|}}{{\left| {\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right]} \right|}}\)
Đề thi liên quan
-
Đề kiểm tra học kì 1 - Đề số 1
-
50 câu hỏi
-
90 phút
-
-
Đề kiểm tra học kì 1 - Đề số 3
-
50 câu hỏi
-
90 phút
-
-
Đề kiểm tra học kì 1 - Đề số 4
-
50 câu hỏi
-
90 phút
-
-
Đề kiểm tra học kì 1 - Đề số 5
-
50 câu hỏi
-
90 phút
-

