Đề kiểm tra 15 phút chương 5: Khối đa diện và thể tích - Đề số 1
-
Hocon247
-
12 câu hỏi
-
45 phút
-
651 lượt thi
-
Dễ
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
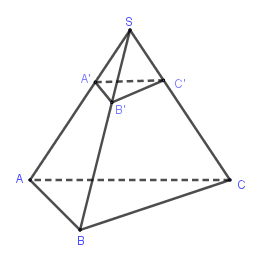
Cho khối chóp \(S.ABC\). Trên các cạnh \(SA,SB,SC\) lấy các điểm \(A',B',C'\) sao cho \(A'A = 2SA',B'B = 2SB',C'C = 2SC'\), khi đó tồn tại một phép vị tự biến khối chóp \(S.ABC\) thành khối chóp \(S.A'B'C'\) với tỉ số đồng dạng là:
Ta có: \(A'A = 2SA',B'B = 2SB',C'C = 2SC' \)
$\Rightarrow \overrightarrow {SA'} = \dfrac{1}{3}\overrightarrow {SA} ,\overrightarrow {SB'} = \dfrac{1}{3}\overrightarrow {SB} ,\overrightarrow {SC'} = \dfrac{1}{3}\overrightarrow {SC} $
Do đó phép vị tự tâm \(S\) tỉ số \(k = \dfrac{1}{3}\) biến các điểm \(A,B,C\) thành \(A',B',C'\).
Giải thích thêm:
Một số em sẽ chọn đáp án D vì nhầm lẫn với phép vị tự biến khối chóp \(S.A'B'C'\) thành khối chóp \(S.ABC\).
Cho hình chóp \(S.ABC\) có \(SA \bot SB,SB \bot SC,SA \bot SC;SA = 2a,SB = b,SC = c\). Thể tích khối chóp là:
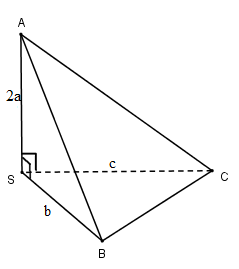
Ta có: \(\left. \begin{array}{l}SA \bot SB\\SA \bot SC\\SB \bot SC\end{array} \right\} \Rightarrow S.ABC\) là tứ diện vuông.
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{6}SA.SB.SC = \dfrac{1}{6}.2a.b.c = \dfrac{1}{3}abc\).
Hướng dẫn giải:
- Sử dụng công thức tính thể tích cho tứ diện vuông \(V = \dfrac{1}{6}abc\) để suy ra đáp án.
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án C vì không chú ý giả thiết \(SA = 2a\), một số em khác thì áp dụng nhầm công thức thể tích của tứ diện vuông \(V = \dfrac{1}{3}abc\) và chọn nhầm đáp án D là sai.
Trong các hình dưới đây, hình nào là khối đa diện?
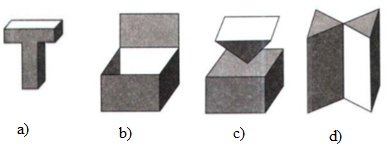
Trong các hình đã cho chỉ có hình a) là khối đa diện.
Hình b) có 3 cạnh ở trên không phải cạnh chung của 2 mặt, hình c) và d) có 1 cạnh là không là cạnh chung của 2 mặt.
Hướng dẫn giải:
Sử dụng tính chất khối đa diện: mối cạnh là cạnh chung của đúng hai mặt.
Giải thích thêm:
Nhiều em sẽ chọn đáp án là hình d). Thuy nhiên vì hình d) có 1 cạnh không là cạnh chung của chỉ 2 mặt nên hình d sai.
Cho khối đa diện lồi có số đỉnh, số mặt và số cạnh lần lượt là \(D,M,C\). Chọn mệnh đề đúng:
Khối đa diện lồi có \(D\) đỉnh, \(M\) mặt và \(N\) cạnh thì \(D - C + M = 2\).
Giải thích thêm:
Một số em sẽ chọn sai đáp án B hặc D vì nhớ nhầm công thức.
Trong các mệnh đề sau, mệnh đề nào sai?
Các hình tứ diện đều, lập phương, bát diện đều là các khối đa diện đều nên chúng là đa diện lồi.
Hình tạo bởi hai tứ diện đều ghép với nhau có thể là đa diện lồi hoặc không phải là đa diện lồi
⇒ Mệnh đề “Hình tạo bởi hai tứ diện đều ghép với nhau là đa diện lồi” là mệnh đề sai
Vật thể nào trong các vật thể sau không phải là khối đa diện?

Quan sát bốn hình, có hình C có cạnh là cạnh chung của 4 đa giác, vậy hình này không phải khối đa diện.
Hướng dẫn giải:
Khái niệm khối đa diện: Khối đa diện là hình được tạo bởi hữu hạn các đa giác thỏa mãn hai điều kiện:
+ Hai đa giác phân biệt chỉ có thể hoặc không giao nhau, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.
+ Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
Giải thích thêm:
Một số em sẽ chọn ngay hình 1 vì thấy đó không phải đa diện lồi nhưng thực chất hình 1 vẫn là khối đa diện.
Chọn khẳng định sai.
Các khẳng định A, C, D đúng
Khẳng định B sai vì hai mặt của khối đa diện có thể có điểm chung hoặc không có điểm chung, chẳng hạn hai mặt đối nhau của hình hộp chữ nhật.
Cho hình chóp đều $S.ABCD$ có cạnh bên và cạnh đáy bằng $a$. Thể tích của khối chóp $S.ABCD$ là:
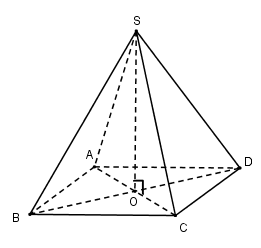
Gọi \(O = AC \cap BD\)
Vì chóp $S.ABCD$ đều nên \(SO \bot \left( {ABCD} \right)\)
Ta có: \(AC = BD = a\sqrt 2 \Rightarrow OA = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OA \Rightarrow \Delta SOA\) vuông tại O \( \Rightarrow SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 2 }}{2}\)
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}\dfrac{{a\sqrt 2 }}{2}{a^2} = \dfrac{{{a^3}\sqrt 2 }}{6}\)
Hướng dẫn giải:
- Bước 1: Tính diện tích đáy \({S_{ABCD}}\)
- Bước 2: Tính chiều cao \(h = SO\).
- Bước 3: Tính thể tích \(V = \dfrac{1}{3}Sh\).
Cho bốn hình sau đây. Mệnh đề nào sau đây sai:
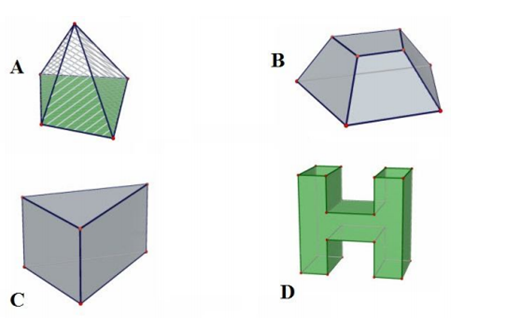
Khối đa diện A là khối chóp tứ giác.
Khối đa diện D không phải là khối đa diện lồi
Khối đa diện B, C là khối đa diện lồi
Cho tứ diện \(ABCD\) có các cạnh \(AB,AC,AD\) đôi một vuông góc với nhau, \(AB = 6a,AC = 7a,AD = 4a\). Gọi \(M,N,P\) lần lượt là trung điểm của các cạnh \(BC,CD,DB\). Thể tích \(V\) của tứ diện \(AMNP\) là:
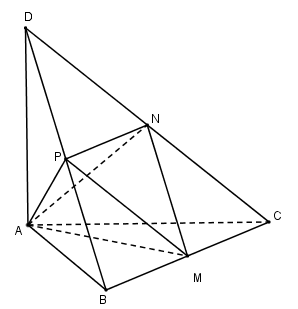
Ta có:
\(ABCD\) là tứ diện vuông tại \(A\) nên \({V_{ABCD}} = \dfrac{1}{6}AB.AC.AD = \dfrac{1}{6}.6a.7a.4a = 28{a^3}\).
Áp dụng công thức tính tỉ lệ thể tích các khối tứ diện ta có:
\(\dfrac{{{V_{DAPN}}}}{{{V_{DABC}}}} = \dfrac{{DA}}{{DA}}.\dfrac{{DP}}{{DB}}.\dfrac{{DN}}{{DC}} = \dfrac{1}{1}.\dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4} \Rightarrow {V_{DAPN}} = \dfrac{1}{4}{V_{DABC}} = \dfrac{1}{4}.28{a^3} = 7{a^3}\)
\(\dfrac{{{V_{BAPM}}}}{{{V_{BADC}}}} = \dfrac{{BA}}{{BA}}.\dfrac{{BP}}{{BD}}.\dfrac{{BM}}{{BC}} = \dfrac{1}{1}.\dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4} \Rightarrow {V_{BAPM}} = \dfrac{1}{4}{V_{BADC}} = \dfrac{1}{4}.28{a^3} = 7{a^3}\)
\(\dfrac{{{V_{CAMN}}}}{{{V_{CABD}}}} = \dfrac{{CA}}{{CA}}.\dfrac{{CM}}{{CB}}.\dfrac{{CN}}{{CD}} = \dfrac{1}{1}.\dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4} \Rightarrow {V_{CAMN}} = \dfrac{1}{4}{V_{CABD}} = \dfrac{1}{4}.28{a^3} = 7{a^3}\)
Do đó \({V_{AMNP}} = {V_{ABCD}} - {V_{DAPN}} - {V_{BAPM}} - {V_{CAMN}} = 28{a^3} - 7{a^3} - 7{a^3} - 7{a^3} = 7{a^3}\)
Hướng dẫn giải:
Tính thể tích các khối chóp ${{V_{DAPN}}}$, ${{V_{BAPM}}}$, ${V_{CAMN}}$ và $ V_{ABCD}$ rồi tính ${V_{AMNP}} = {V_{ABCD}} - {V_{DAPN}} $ $- {V_{BAPM}} - {V_{CAMN}}$
Giải thích thêm:
- Một số em sẽ tính nhầm tỉ lệ thể tích khối tứ diện \(AMNP\) và \(ABCD\) là \(\dfrac{1}{3}\) nên chọn nhầm đáp án C là sai.
- Cách giải ở trên hướng dẫn các em tính thể tích tứ diện bằng phương pháp cộng trừ thể tích (phân chia khối đa diện) và cách áp dụng công thức tỉ lệ thể tích.
Ngoài ra, bài toán còn một cách giải khác, các em có thể tham khảo các bước giải như sau:
+ Tính thể tích của tứ diện \(ABCD\)
+ So sánh diện tích các tam giác \(MNP\) và \(BCD\), cụ thể \({S_{MNP}} = \dfrac{1}{4}{S_{BCD}}\)
+ So sánh thể tích \({V_{A.MNP}}\) và \({V_{A.BCD}}\), cụ thể:
Hai tứ diện có chung chiều cao kẻ từ \(A\) và diện tích đáy \({S_{MNP}} = \dfrac{1}{4}{S_{BCD}}\)
Do đó \({V_{A.MNP}} = \dfrac{1}{4}{V_{A.BCD}}\)
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\). Biết \(AC = a\sqrt 2 \), cạnh \(SC\) tạo với đáy một góc \({60^0}\) và diện tích tứ giác \(ABCD\) là \(\dfrac{{3{a^2}}}{2}\). Gọi \(H\) là hình chiếu của \(A\) trên cạnh \(SC\). Tính thể tích khối chóp \(H.ABCD\).
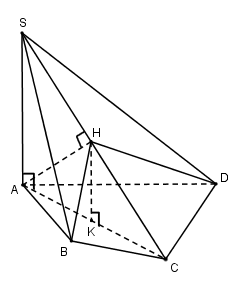
Ta có: \(SA \bot \left( {ABCD} \right) \Rightarrow AC\)là hình chiếu của $SC$ trên \(\left( {ABCD} \right) \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {\left( {SC;AC} \right)} = {60^0}\)
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow \Delta SAC\) vuông tại $A$ và $\widehat {SCA} = {60^0}$
Xét tam giác vuông $SAC$ có: \(SA = AC.\tan 60 = a\sqrt 2 .\sqrt 3 = a\sqrt 6 ;\,SC = \dfrac{{AC}}{{{\rm{cos60}}}} = \dfrac{{a\sqrt 2 }}{{\dfrac{1}{2}}} = 2a\sqrt 2 \)
Áp dụng hệ thức lượng trong tam giác vuông $SAC$ có: \(A{C^2} = HC.SC \Rightarrow \dfrac{{HC}}{{SC}} = \dfrac{{A{C^2}}}{{S{C^2}}} = \dfrac{{2{a^2}}}{{8{a^2}}} = \dfrac{1}{4}\)
Trong $\left( {SAC} \right)$ kẻ \(HK//SA \Rightarrow HK \bot \left( {ABCD} \right)\)
Ta có: \(\dfrac{{HK}}{{SA}} = \dfrac{{HC}}{{SC}} = \dfrac{1}{4} \Rightarrow HK = \dfrac{1}{4}SA = \dfrac{{a\sqrt 6 }}{4}\)
Vậy \({V_{H.ABCD}} = \dfrac{1}{3}HK.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 6 }}{4}.\dfrac{{3{a^2}}}{2} = \dfrac{{{a^3}\sqrt 6 }}{8}\)
Hướng dẫn giải:
- Xác định góc giữa \(SC\) và mặt phẳng đáy: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
- Dựng đường cao \(HK\) của hình chóp \(H.ABCD\) và tính độ dài \(HK\) dựa vào định lý Ta-let.
- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\).
Cho hình chóp tứ giác đều $S.ABCD$ có chiều cao $h$, góc ở đỉnh của mặt bên bằng \({60^0}\). Thể tích hình chóp là:
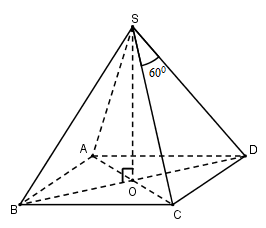
Gọi \(O = AC \cap BD\).
Vì chóp $S.ABCD$ đều nên \(SO \bot \left( {ABCD} \right)\)
Đặt \(SA = SB = SC = SD = a\)
Tam giác $SCD$ có:\(SC = SD;\widehat {CSD} = {60^0} \Rightarrow \Delta SCD\) đều\( \Rightarrow CD = SC = SD = a\)
\( \Rightarrow \) Hình vuông $ABCD$ cạnh \(a \Rightarrow AC = BD = a\sqrt 2 \Rightarrow OC = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OC \Rightarrow \Delta SOC\) vuông tại $O$
\( \Rightarrow SO = \sqrt {S{C^2} - O{C^2}} \Rightarrow h = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 2 }}{2} \Rightarrow a = h\sqrt 2 \)
\( \Rightarrow {S_{ABCD}} = {a^2} = {\left( {h\sqrt 2 } \right)^2} = 2{h^2}\)
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}h.2{h^2} = \dfrac{{2{h^3}}}{3}\)
Hướng dẫn giải:
- Bước 1: Tính diện tích đáy \(S\)
- Bước 2: Tính chiều cao \(h\).
- Bước 3: Tính thể tích \(V = \dfrac{1}{3}Sh\).
Đề thi liên quan
-
Đề kiểm tra 15 phút chương 5: Khối đa diện và thể tích - Đề số 2
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 15 phút chương 5: Khối đa diện và thể tích - Đề số 3
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 1 tiết chương 5: Khối đa diện và thể tích - Đề số 1
-
25 câu hỏi
-
45 phút
-
-
Đề kiểm tra 1 tiết chương 5: Khối đa diện và thể tích - Đề số 2
-
25 câu hỏi
-
45 phút
-
-
Đề kiểm tra 1 tiết chương 5: Khối đa diện và thể tích - Đề số 3
-
25 câu hỏi
-
45 phút
-

