Đề kiểm tra học kì 1 - Đề số 1
-
Hocon247
-
50 câu hỏi
-
90 phút
-
658 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Tìm tất cả các giá trị thực của $m$ để hàm số $y = {x^4} + 2\left( {{m^2} - 9} \right){x^2} + 5m + 2$ có cực đại, cực tiểu
Ta có: $y = {x^4} + 2\left( {{m^2} - 9} \right){x^2} + 5m + 2 \Rightarrow y' = 4{x^3} + 4x\left( {{m^2} - 9} \right) = 4x\left( {{x^2} + {m^2} - 9} \right)$
$y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} = 9 - {m^2}\left( 1 \right)}\end{array}} \right.$
Hàm số đã cho có cực đại, cực tiểu khi và chỉ khi phương trình $\left( 1 \right)$có hai nghiệm phân biệt khác 0
$ \Leftrightarrow 9 - {m^2} > 0 \Leftrightarrow {\rm{\;}} - 3 < m < 3$
Hướng dẫn giải:
Áp dụng lý thuyết về cực đại, cực tiểu của hàm trùng phương
Điều kiện để biểu thức \({\log _2}\left( {3 - x} \right)\) xác định là:
Để biểu thức \({\log _2}\left( {3 - x} \right)\) xác định thì \(3 - x > 0 \Leftrightarrow x < 3\)
Hướng dẫn giải:
Điều kiện để \({\log _a}b\) xác định là \(b > 0\).
Chọn mệnh đề đúng:
Giới hạn cần nhớ: \(\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln \left( {1 + x} \right)}}{x} = 1\)
Nếu $\mathop {\lim }\limits_{x \to x_0^ + } y = + \infty $ thì đường thẳng $x = {x_0}$ là:
Nếu $\mathop {\lim }\limits_{x \to x_0^ + } y = + \infty $ thì đường thẳng $x = {x_0}$ là tiệm cận đứng của đồ thị hàm số.
Hình chóp nào sau đây luôn nội tiếp được mặt cầu?
Trong các hình chóp tam giác, tứ giác, ngũ giác, lục giác thì chỉ có tam giác luôn nội tiếp được đường tròn nên hình chóp tam giác luôn nội tiếp được mặt cầu.
Hướng dẫn giải:
Hình chóp có đáy là đa giác nội tiếp được đường tròn thì sẽ nội tiếp được mặt cầu.
Cho hàm số \(y = \dfrac{{2018}}{{x - 2}}\) có đồ thị \(\left( H \right).\) Số đường tiệm cận của \(\left( H \right)\) là:
Ta có \(\mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} \infty } y = \mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} \infty } \dfrac{{2018}}{{x - 2}} = 0 \Rightarrow {\mkern 1mu} {\mkern 1mu} y = 0\) là tiệm cận ngang của đồ thị hàm số.
Và \(\mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} 2} y = \mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} 2} \dfrac{{2018}}{{x - 2}} = \infty {\rm{\;}} \Rightarrow {\mkern 1mu} {\mkern 1mu} x = 2\) là tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có \(2\) đường tiệm cận.
Hướng dẫn giải:
Dựa vào định nghĩa tính giới hạn tìm tiệm cận của đồ thị hàm số
+) Nếu \(\mathop {\lim }\limits_{x \to \infty } y = a \Rightarrow y = a\) là TCN của đồ thị hàm số.
+) Nếu \(\mathop {\lim }\limits_{x \to {x_0}} y = \infty {\rm{\;}} \Rightarrow x = {x_0}\) là TCĐ của đồ thị hàm số.
Công thức tính thể tích khối nón có bán kính đáy \(r\), độ dài đường sinh \(l\) và chiều cao \(h\) là:
Công thức tính thể tích khối nón: \(V = \dfrac{1}{3}\pi {r^2}h\)
Số cực trị của hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) là:
Hàm phân thức bậc nhất trên bậc nhất không có cực trị.
Điểm nào sau đây không thuộc đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\)?
- Đồ thị hàm số luôn đi qua các điểm \(\left( {1;0} \right)\) và \(\left( {a;1} \right)\).
- Với \(x = {a^2}\) thì \(y = {\log _a}x = {\log _a}{a^2} = 2\) nên đồ thị hàm số đi qua \(\left( {{a^2};2} \right)\) nên C sai, D đúng.
Hướng dẫn giải:
Sử dụng điều kiện để điểm thuộc đồ thị hàm số là tọa độ điểm đó thỏa mãn phương trình của hàm số.
Giải thích thêm:
Khi thay \(x = {a^2}\), nhiều HS sẽ tính nhầm \(y = {\log _a}{a^2} = {\log _a}\left( {a.a} \right) = a\) là sai.
Cho \(m\) là số nguyên âm. Chọn kết luận đúng:
Vì \(1 < \dfrac{6}{5} < \dfrac{5}{4}\) và \(m\) nguyên âm nên \({1^m} > {\left( {\dfrac{6}{5}} \right)^m} > {\left( {\dfrac{5}{4}} \right)^m} \Leftrightarrow 1 > {\left( {\dfrac{6}{5}} \right)^m} > {\left( {\dfrac{5}{4}} \right)^m}\).
Hướng dẫn giải:
Sử dụng hệ quả so sánh lũy thừa:
Với \(0 < a < b\) và \(m\) là số nguyên âm thì: \({a^m} > {b^m}\).
Chọn mệnh đề đúng:
Nếu \(\left( P \right)\) là mặt phẳng kính thì \(OH = 0\left( {H \equiv O} \right)\) hay \(\left( P \right)\) đi qua \(O\) là tâm mặt cầu, do đó \(\left( P \right)\) đi qua đường kính của mặt cầu.
Giải thích thêm:
Một số em chọn nhầm đáp án D vì nghĩ mặt phẳng kính đi qua tâm mặt cầu nhưng không đi qua điểm nào thuộc mặt cầu là sai.
Hàm số nào có thể có đồ thị dạng như hình vẽ?
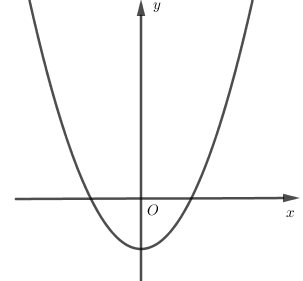
Dạng đồ thị đã cho có thể là của hàm số bậc hai hoặc hàm bậc bốn trùng phương.
Hướng dẫn giải:
Quan sát dạng đồ thị và đối chiếu với các đáp án bài cho.
Điểm \(M\) thuộc mặt cầu tâm \(O\) bán kính \(R\) nếu:
Điểm \(M\) thuộc mặt cầu tâm \(O\) bán kính \(R\) nếu \(OM = R\).
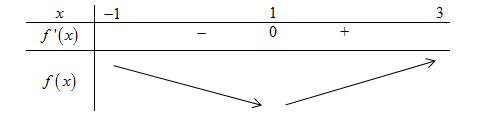
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình vẽ, chọn kết luận đúng:
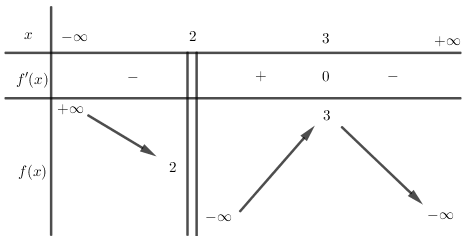
Từ bảng biến thiên ta thấy: $f'\left( x \right) > 0$ trên $\left( {2;3} \right)$ nên hàm số đồng biến trên $\left( {2;3} \right)$.
$f'\left( x \right) < 0$ trên $\left( { - \infty ;2} \right)$ và $\left( {3; + \infty } \right)$ nên hàm số nghịch biến trên các khoảng $\left( { - \infty ;2} \right)$ và $\left( {3; + \infty } \right)$.
Hướng dẫn giải:
Sử dụng định lý:
Định lý: Cho hàm số $y = f\left( x \right)$ xác định và có đạo hàm trên $K$.
a) Nếu $f'\left( x \right) > 0,\forall x \in K$ thì hàm số $y = f\left( x \right)$ đồng biến trên $K$.
b) Nếu $f'\left( x \right) < 0,\forall x \in K$ thì hàm số $y = f\left( x \right)$ nghịch biến trên $K$.
Giải thích thêm:
HS thường nhầm lẫn khi quan sát bảng biến thiên, một số bạn thấy chiều mũi tên đi từ $ - \infty $ lên $3$ rồi vội vàng kết luận hàm số đồng biến trên $\left( { - \infty ;3} \right)$ dẫn đến chọn sai đáp án.
Trong các hàm số sau đây, hàm số nào đồng biến trên các khoảng xác định?
Hàm số \(y = {x^{ - 4}}\) có tập xác định là \(\mathbb{R}\backslash \left\{ 0 \right\}\) và có \(y' = - 4{x^{ - 5}}\) nên không đồng biến trên các khoảng xác định (đồng biến trên \(\left( { - \infty ,0} \right)\) và nghịch biến trên \(\left( {0, + \infty } \right)\)), loại A.
Hàm số \(y = {x^{ - \dfrac{3}{4}}}\) có tập xác định là \(\left( {0, + \infty } \right)\) và có \(y' = - \dfrac{3}{4}{x^{ - \dfrac{7}{4}}} < 0,\forall x \in \left( {0, + \infty } \right)\) nên không đồng biến trên từng khoảng xác định, loại B.
Hàm số \(y = {x^4}\) có tập xác định là \(\mathbb{R}\) và có \(y' = 4{x^3}\) nên không đồng biến trên các khoảng xác định, loại C.
Hàm số \(y = \sqrt[3]{x}\) có tập xác định là \(\mathbb{R}\) và có \(y' = \dfrac{1}{{3\sqrt[3]{{{x^2}}}}} > 0\) nên hàm số đồng biến trên các khoảng xác định.
Hướng dẫn giải:
Tính đạo hàm của mỗi hàm số rồi xét dấu đạo hàm trên khoảng xác định \(D\).
Nếu \(y' \ge 0\) và bằng \(0\) tại hữu hạn điểm thuộc \(D\) thì hàm số đồng biến trên \(D\).
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sin x$ trên đoạn $\left[ { - \dfrac{\pi }{2}; - \dfrac{\pi }{3}} \right]$ lần lượt là
Ta có $y' = \cos x \Rightarrow y' = 0 \Leftrightarrow \cos x = 0 \Leftrightarrow x = \dfrac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)$
Do $x\in \left[ { - \dfrac{\pi }{2}; - \dfrac{\pi }{3}} \right]$ nên $k=-1$ hay $x=-\dfrac{\pi }{2}$
Suy ra $y\left( { - \dfrac{\pi }{2}} \right) = - 1;\;\;y\left( { - \dfrac{\pi }{3}} \right) = - \dfrac{{\sqrt 3 }}{2} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\rm{\;}}&{\mathop {\max}\limits_{\left[ { - \frac{\pi }{2}; - \frac{\pi }{3}} \right]}y = - \dfrac{{\sqrt 3 }}{2}}\\{{\rm{ \;}}}&{\mathop {\min }\limits_{\left[ { - \frac{\pi }{2}; - \frac{\pi }{3}} \right]} y = - 1}\end{array}} \right.$
Hướng dẫn giải:
+) Tính đạo hàm y' và giải phương trình $y' = 0$ tìm các nghiệm ${x_i}.$
+) Tìm giá trị lớn nhất của hàm số $y = f\left( x \right)$ trên đoạn $\left[ {a;\;b} \right],$ ta tính các giá trị $y\left( a \right);\;y\left( {{x_i}} \right);\;\;y\left( b \right)$ và đưa ra kết luận đúng.
Giải thích thêm:
Các em có thể nhận xét ngay hàm số \(y = \sin x\) đồng biến trên đoạn $\left[ { - \dfrac{\pi }{2}; - \dfrac{\pi }{3}} \right]$, từ đó tìm được GTLN, GTNN của hàm số.
Cho a là số thực dương. Mệnh đề nào dưới đây đúng
Ta có: \({\log _2}{a^3} = 3{\log _2}a\)
Hướng dẫn giải:
Áp dụng công thức logarit: \({\log _a}{b^n} = n{\log _a}b\left( {b > 0} \right)\)
Hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ, chọn kết luận đúng:
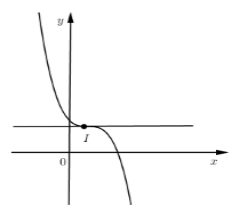
Quan sát đồ thị ta thấy \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty ;\mathop {\lim }\limits_{x \to - \infty } y = + \infty \) nên \(a < 0\).
Cho \(a > 0,a \ne 1\). Tìm mệnh đề đúng trong các mệnh đề sau:
Cho \(a > 0;a \ne 1\) khi đó hàm số \(y = {a^x}\) có tập xác định là \(R\) , tập giá trị là \(\left( {0; + \infty } \right)\)
Hàm số \(y = {\log _a}x\) có tập xác định là \(\left( {0; + \infty } \right)\) , tập giá trị là \(R\)
Suy ra B đúng
Hướng dẫn giải:
Sử dụng các tính chất của hàm số mũ, hàm số logarit.
Cho biết GTLN của hàm số $f\left( x \right)$ trên $\left[ {1;3} \right]$ là $M = - 2$. Chọn khẳng định đúng:
Nếu $M = - 2$ là GTLN của hàm số $y = f\left( x \right)$ trên $\left[ {1;3} \right]$ thì $f\left( x \right) \leqslant - 2,\forall x \in \left[ {1;3} \right]$.
Cho khối nón có độ dài đường sinh bằng \(2a\) và bán kính đáy bằng \(a\). Thể tích của khối nón đã cho bằng
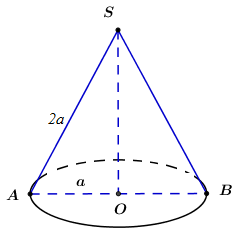
Xét \(\Delta SAO\) vuông tại \(O\) có: \(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {{{\left( {2a} \right)}^2} - {a^2}} = a\sqrt 3 .\)
Khi đó ta có: \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi .{a^2}.a\sqrt 3 = \dfrac{{\pi {a^3}\sqrt 3 }}{3}.\)
Hướng dẫn giải:
+) Sử dụng công thức: \(h = \sqrt {{l^2} - {R^2}} .\)
+) Thể tích hình nón có bán kính R và đường cao h là: \(V = \dfrac{1}{3}\pi {R^2}h.\)
Cho khối chóp có thể tích \(V\), diện tích đáy là \(S\) và chiều cao \(h\). Chọn công thức đúng:
Công thức tính thể tích khối chóp \(V = \dfrac{1}{3}Sh\).
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án D vì nhớ nhầm công thức.
Hãy chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống mệnh đề sau trở thành mệnh đề đúng:
“Số cạnh của một hình đa diện luôn……………….số mặt của hình đa diện ấy”
Hình tứ diện có \(6\) cạnh và \(4\) đỉnh nên số cạnh của tứ diện lớn hơn số mặt của nó.
Hướng dẫn giải:
Sử dụng phương pháp chọn điểm rơi, lấy ví dụ cho hình tứ diện để chọn đáp án.
Giải thích thêm:
Một số em sẽ nhầm lẫn với trường hợp số đỉnh và số mặt của tứ diện nên sẽ chọn đáp án C là sai.
Chọn so sánh đúng:
Ta có: \(5 > 1\) nên \({5^m} > {5^n} \Leftrightarrow m > n\).
Hướng dẫn giải:
Sử dụng tính chất của lũy thừa: Với \(a > 1\) thì \({a^m} > {a^n} \Leftrightarrow m > n\)
Hàm số \(y = - {x^3} + {x^2} + 1\,\) xác định khi:
Hàm số \(y = - {x^3} + {x^2} + 1\,\) xác định với mọi \(x \in \mathbb{R}\)
Hướng dẫn giải:
Hàm đa thức bậc ba xác định trên tập số thực.
Đường cong ở hình bên là đồ thị hàm số \(y=\dfrac{ax+2}{cx+b}\) với \(a,b,c\) là các số thực. Mệnh đề nào sau đây đúng?
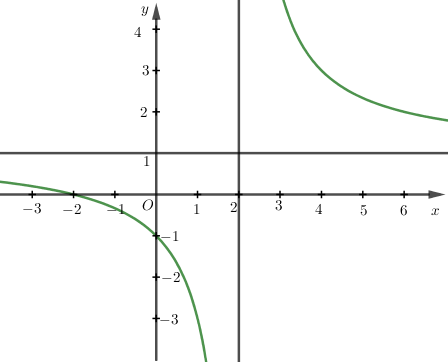
Vì đồ thị hàm số nhận đường thẳng \(y=1;x=2\) làm đường tiệm cận ngang và tiệm cận đứng và đồ thị hàm số cắt \(Oy\) tại điểm có tung độ bằng \(-1\) nên ta có hệ :
\(\left\{ {\begin{array}{*{20}{c}}{ - \dfrac{b}{c} = 2}\\{\dfrac{a}{c} = 1}\\{\dfrac{2}{b} = - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b = - 2}\\{c = 1}\end{array}} \right.\).
Hướng dẫn giải:
Sử dụng kiến thức về tiệm cận và giao của đồ thị hàm số với các trục tọa độ
Cho hàm số \(y = f\left( x \right)\) xác định và có đạo hàm \(f'\left( x \right) = {x^2} + 2\) trên \(R\), chọn kết luận đúng:
Ta có: \(f'\left( x \right) = {x^2} + 2 > 0,\forall x \in R\) nên hàm số đồng biến trên \(R\).
Hướng dẫn giải:
Sử dụng định lý: “Nếu \(f'\left( x \right) > 0,\forall x \in K\) thì hàm số \(y = f\left( x \right)\) đồng biến trên \(K\)”.
Cho \(x > 0\) và \(n \in {\mathbb{N}^*},n \ge 2\). Chọn công thức đúng:
Ta có: \(\left( {\sqrt[n]{x}} \right)' = \left( {{x^{\dfrac{1}{n}}}} \right)' = \dfrac{1}{n}{x^{\dfrac{1}{n} - 1}} = \dfrac{1}{n}{x^{\dfrac{{1 - n}}{n}}} = \dfrac{1}{n}{x^{ - \dfrac{{n - 1}}{n}}}\)
Hướng dẫn giải:
Sử dụng điều kiện để đẳng thức \(\sqrt[n]{x} = {x^{\dfrac{1}{n}}}\) xảy ra là \(x > 0\) và công thức tính đạo hàm \(\left( {{x^\alpha }} \right)' = \alpha {x^{\alpha - 1}}\)
Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác cân tại \(A\), biết \(SA \bot \left( {ABC} \right)\), \(BC = 2a,\widehat {BAC} = {120^0}\), góc giữa mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) bằng \({45^0}\). Tính thể tích khối chóp \(S.ABC\).
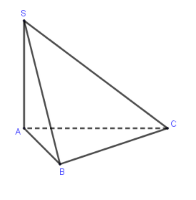
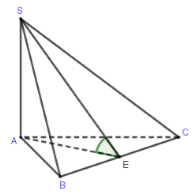
Gọi \(E\) là trung điểm của \(BC\) \( \Rightarrow \left\{ \begin{array}{l}AE \bot BC\\SA \bot BC\end{array} \right. \Rightarrow BC \bot \left( {SAE} \right) \Rightarrow BC \bot SE\)
Ta có: \(\left\{ \begin{array}{l}AE \bot BC\\SE \bot BC\\\left( {ABC} \right) \cap \left( {SBC} \right) = BC\end{array} \right. \Rightarrow \angle \left( {\left( {ABC} \right);\left( {SBC} \right)} \right) = \angle SEA = {45^0}.\)
\( \Rightarrow \Delta SAE\) vuông cân tại \(A \Rightarrow SA = AE\).
Tam giác \(ABC\) cân tại \(A\) có \(\widehat A = {120^0},BC = 2a\),
\(AE\) là tia phân giác của \(\widehat A\) \( \Rightarrow \widehat {BAE} = {60^0}\).
Tam giác vuông \(AEB\) có \(\widehat {BAE} = {60^0},BE = \dfrac{1}{2}BC = a \Rightarrow AE = \dfrac{{BE}}{{\tan {{60}^0}}} = \dfrac{{BE}}{{\sqrt 3 }} = \dfrac{{a\sqrt 3 }}{3} = SA\).
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}.SA.\dfrac{1}{2}AE.BC = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{3}.\dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{3}.2a = \dfrac{{{a^3}}}{9}\).
Hướng dẫn giải:
- Xác định góc giữa hai mặt phẳng: là góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến.
- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao.
Hình dưới đây là đồ thị của hàm số nào?

Dựa vào đồ thị hàm số ta thấy đồ thị hàm số có dạng là 1 parabol có đỉnh là \(\left( {0; - 2} \right) \Rightarrow \) loại đáp án A, D.
Đồ thị hàm số đi qua các điểm \(\left( {1;\,\,0} \right)\) và \(\left( { - 1;\,\,0} \right),\) thay tọa độ các điểm này vào công thức hàm số ở đáp án B và C thấy chỉ có đáp án B thỏa mãn.
có 1 điểm cực trị có tọa là \(\left( {0; - 2} \right)\)
Hướng dẫn giải:
Dựa vào đồ thị hàm số, nhận biết các điểm thuộc đồ thị hàm số và các điểm cực trị của đồ thị từ đó chọn đáp án đúng.
Hàm số $y = - {x^4} - 2{x^2} + 3$ nghịch biến trên:
TXĐ: $R$.
Ta có:
\(y'=-4x^3-4x=-4x(x^2+1)\)
\(\Rightarrow y' = 0 \Leftrightarrow x = 0\)
Ta có bảng biến thiên
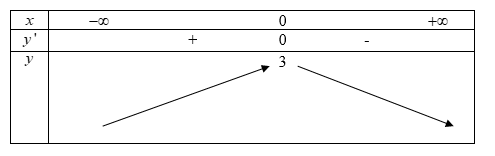
Từ bảng biến thiên ta thấy hàm nghịch biến trên khoảng $\left( {0; + \infty } \right)$.
Hướng dẫn giải:
- Bước 1: Tìm TXĐ của hàm số.
- Bước 2: Tính đạo hàm $f'\left( x \right)$, tìm các điểm ${x_1},{x_2},...,{x_n}$ mà tại đó đạo hàm bằng $0$ hoặc không xác định.
- Bước 3: Xét dấu đạo hàm và nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
+ Các khoảng mà $f'\left( x \right) > 0$ là các khoảng đồng biến của hàm số.
+ Các khoảng mà $f'\left( x \right) < 0$ là các khoảng nghịch biến của hàm số.
Cho hàm số $y = \dfrac{1}{3}{x^3} - m{x^2} + (2m - 4)x - 3.$ Tìm $m$ để hàm số có các điểm cực đại, cực tiểu ${x_1};{x_2}$ thỏa mãn: $x_1^2 + x_2^2 = {x_1}.{x_2} + 10$
\(y' = {x^2} - 2mx + 2m - 4\)
Để hàm số có cực đại cực tiểu \( \Leftrightarrow \Delta ' > 0,\forall m \Leftrightarrow {m^2} - 2m + 4 > 0,\forall m\)
Khi đó phương trình $y'=0$ có hai nghiệm $x_1,x_2$ thỏa mãn
\(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a} = 2m\\{x_1}{x_2} = \dfrac{c}{a} = 2m - 4\end{array} \right.\)
Ta có:
\(\begin{array}{l}x_1^2 + x_2^2 = {x_1}.{x_2} + 10\\ \Leftrightarrow {({x_1} + {x_2})^2} - 2{x_1}{x_2} - {x_1}{x_2} - 10 = 0\\ \Leftrightarrow {({x_1} + {x_2})^2} - 3{x_1}{x_2} - 10 = 0\\ \Leftrightarrow {(2m)^2} - 3.(2m - 4) - 10 = 0\\ \Leftrightarrow 4{m^2} - 6m + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = \dfrac{1}{2}\end{array} \right.\end{array}\)
Hướng dẫn giải:
- Bước 1: Tính $y'$.
- Bước 2: Tìm điều kiện để hàm số có hai cực trị $ \Leftrightarrow y' = 0$ có hai nghiệm phân biệt.
- Bước 3: Sử dụng hệ thức Vi-et để thay $\left\{ \begin{gathered} {x_1} + {x_2} = S \hfill \\{x_1}{x_2} = P \hfill \\\end{gathered} \right.$ và tìm $m$.
Cho hàm số $y = \dfrac{{2x + 2017}}{{\left| x \right| + 1}}.$ Mệnh đề nào là đúng?
Ta có: $\mathop {\lim }\limits_{x \to + \infty } {\mkern 1mu} y = \mathop {\lim }\limits_{x \to + \infty } {\mkern 1mu} \dfrac{{2x + 2017}}{{x + 1}} = \mathop {\lim }\limits_{x \to + \infty } {\mkern 1mu} \dfrac{{2 + \dfrac{{2017}}{x}}}{{1 + \dfrac{1}{x}}} = 2 \Rightarrow y = 2$ là TCN
$\mathop {\lim }\limits_{x \to - \infty } {\mkern 1mu} y = \mathop {\lim }\limits_{x \to - \infty } {\mkern 1mu} \dfrac{{2x + 2017}}{{ - x + 1}} = \mathop {\lim }\limits_{x \to + \infty } {\mkern 1mu} \dfrac{{2 + \dfrac{{2017}}{x}}}{{ - 1 + \dfrac{1}{x}}} = 2 \Rightarrow y = - 2$ là TCN.
Vậy đồ thị hàm số có $2$ tiệm cận ngang là các đường thẳng $y = - 2;y = 2$.
Hướng dẫn giải:
Sử dụng định nghĩa tiệm cận:
+) Đường thẳng $y = a$ là tiệm cận ngang của đồ thị hàm số $y = f\left( x \right)$ khi một trong hai điều kiện sau được thỏa mãn$\mathop {\lim }\limits_{x \to + \infty } {\mkern 1mu} y = a;\mathop {\lim }\limits_{x \to - \infty } {\mkern 1mu} y = a$.
+) Đường thẳng $x = b$ là tiệm cận đứng của đồ thị hàm số $y = f\left( x \right)$ khi một trong bốn điều kiện sau được thỏa mãn$\mathop {\lim }\limits_{x \to {b^ + }} {\mkern 1mu} y = + \infty ;\mathop {\lim }\limits_{x \to {b^ - }} {\mkern 1mu} y = + \infty ;\mathop {\lim }\limits_{x \to {b^ - }} {\mkern 1mu} y = + \infty ;\mathop {\lim }\limits_{x \to {b^ - }} {\mkern 1mu} y = - \infty $.
Cho hàm số \(y = f\left( x \right)\) có hai giá trị cực đại, cực tiểu thỏa mãn \({y_{CD}}.{y_{CT}} = 0\). Khi đó:
Vì \({y_{CD}}.{y_{CT}} = 0 \Leftrightarrow \left[ \begin{array}{l}{y_{CD}} = 0\\{y_{CT}} = 0\end{array} \right.\) hay một trong hai điểm cực trị của đồ thị hàm số nằm trên trục hoành.
Khi đó đồ thị hàm số chỉ có \(2\) giao điểm chung với \(Ox\)
Giải thích thêm:
HS thường nhầm lẫn rằng \({y_{CT}} < 0 < {y_{CD}}\) nên đường thẳng \(y = 0\) chỉ cắt đồ thị hàm số tại 1 điểm duy nhất và chọn ngay đáp án C mà không để ý đến các nhánh còn lại của đồ thị hàm số.
Cho hàm số $y = f\left( x \right)$ có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng?
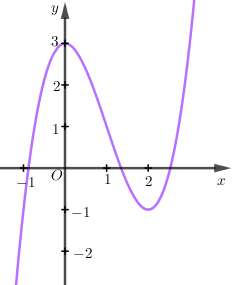
A sai vì $y=3$ là giá trị cực đại của hàm số, không phải giá trị lớn nhất.
B sai vì hàm số đồng biến trên các khoảng $\left( { - \infty ;0} \right),\left( {2; + \infty } \right)$.
C sai vì $x=2$ là điểm cực tiểu của hàm số không phải giá trị cực tiểu.
D đúng vì trên đoạn $\left[ {0;4} \right]$ thì hàm số đạt GTNN (cũng là giá trị cực tiểu) bằng $ - 1$ đạt được tại $x = 2$.
Hướng dẫn giải:
Quan sát đồ thị hàm số và rút ra các nhận xét về cực đại, cực tiểu, GTLN, GTNN, khoảng đồng biến, nghịch biến.
Cho hàm số $y = {x^4} - 2(m + 1){x^2} + m + 2$ có đồ thị $\left( C \right)$. Gọi $\Delta $ là tiếp tuyến với đồ thị $\left( C \right)$ tại điểm thuộc $\left( C \right)$ có hoành độ bằng $1$. Với giá trị nào của tham số $m$ thì $\Delta $ vuông góc với đường thẳng $d:y = - \dfrac{1}{4}x - 2016$
Ta có: $y' = 4{{\text{x}}^3} - 4\left( {m + 1} \right)x$$ \Rightarrow y'\left( 1 \right) = - 4m$
Vì tiếp tuyến $\Delta $ vuông góc với đường thẳng $d$ nên \(k.\left( { - \dfrac{1}{4}} \right) = - 1 \Leftrightarrow k = 4 = y'\left( 1 \right) =-4m\)
Vậy $m$ thỏa mãn đề bài là $m = - 1$
Hướng dẫn giải:
- Tìm hệ số góc của tiếp tuyến tại điểm có hoành độ bằng $1$.
Hệ số góc của tiếp tuyến tại điểm có hoành độ $x = {x_0}$ là $k = y'\left( {{x_0}} \right)$.
- Tiếp tuyến vuông góc với đường thẳng $d \Leftrightarrow k.k' = - 1$ với $k'$ là hệ số góc của $d$.
Giải thích thêm:
HS thường nhầm lẫn điều kiện để hai đường thẳng vuông góc là tích các hệ số góc bằng $1$ dẫn đến chọn nhầm đáp án C.
Biết rằng hàm số \(f\left( x \right) = \sqrt x \ln x\) đạt giá trị lớn nhất trên đoạn \(\left[ {1;e} \right]\) tại \(x = {x_0}\). Mệnh đề nào sau đây là đúng?
Hàm số xác định và liên tục trên đoạn \(\left[ {1;e} \right]\).
Đạo hàm \(f'\left( x \right) = \left( {\sqrt x } \right)'.\ln x + \sqrt x .\left( {\ln x} \right)'\)\( = \dfrac{{\ln x}}{{2\sqrt x }} + \dfrac{1}{{\sqrt x }} = \dfrac{{\ln x + 2}}{{2\sqrt x }}\)
Suy ra \(f'\left( x \right) = 0 \Leftrightarrow \ln x + 2 = 0 \Leftrightarrow \ln x = - 2\)\( \Leftrightarrow x = {e^{ - 2}} = \dfrac{1}{{{e^2}}} \notin \left[ {1;e} \right]\)
Ta có \(\left\{ \begin{array}{l}f\left( 1 \right) = 0\\f\left( e \right) = \sqrt e \end{array} \right.\) \( \Rightarrow \mathop {\max }\limits_{\left[ {1;e} \right]} f\left( x \right) = f\left( e \right) = \sqrt e \).
Do đó \(x_0=e\).
Hướng dẫn giải:
- Tính \(f'\left( x \right)\) và giải phương trình \(f'\left( x \right) = 0\) tìm nghiệm \({x_i} \in \left[ {1;{e}} \right]\)
- Tính các giá trị \(f\left( 1 \right),f\left( {{e}} \right)\) và \(f\left( {{x_i}} \right)\).
- So sánh các kết quả tìm \(\max ,\min f\left( x \right)\) và kết luận.
Tính tổng \(T\) tất cả các nghiệm của phương trình \({4.9^x} - {13.6^x} + {9.4^x} = 0\).
\(\begin{array}{l}{4.9^x} - {13.6^x} + {9.4^x} = 0 \Leftrightarrow 4 - 13.{\left( {\dfrac{2}{3}} \right)^x} + 9.{\left( {\dfrac{2}{3}} \right)^{2x}} = 0 \Leftrightarrow \left[ \begin{array}{l}{\left( {\dfrac{2}{3}} \right)^x} = 1\\{\left( {\dfrac{2}{3}} \right)^x} = \dfrac{4}{9}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right. \Rightarrow T = 0 + 2 = 2\end{array}\)
Hướng dẫn giải:
- Chia cả hai vế cho $9^x$.
- Giải phương trình bậc hai ẩn ${\left( {\dfrac{2}{3}} \right)^x}$.
Giải thích thêm:
Các em cũng có thể đặt $t={\left( {\dfrac{2}{3}} \right)^x}$ để tiện trình bày, tránh nhầm lẫn khi tính toán.
Tập nghiệm của bất phương trình \({3^{\sqrt {2x} + 1}} - {3^{x + 1}} \le {x^2} - 2x\) là:
ĐK: \(x \ge 0\)
${3^{\sqrt {2x} + 1}} - {3^{x + 1}} \le {x^2} - 2x \Leftrightarrow {3^{\sqrt {2x} + 1}} + 2x \le {3^{x + 1}} + {x^2} \Leftrightarrow {3^{\sqrt {2x} + 1}} + {\left( {\sqrt {2x} } \right)^2} \le {3^{x + 1}} + {x^2}$
Xét hàm số \(f\left( t \right) = {3^{t + 1}} + {t^2}\) có \(f'\left( t \right) = {3^{t + 1}}.\ln 3 + 2t > 0\,\,\forall t \ge 0 \Rightarrow \) Hàm số đồng biến trên \(\left[ {0; + \infty } \right)\)
Mà \(f\left( {\sqrt {2x} } \right) \le f\left( x \right) \Leftrightarrow \sqrt {2x} \le x \Leftrightarrow 2x \le {x^2} \Leftrightarrow {x^2} - 2x \ge 0 \Leftrightarrow x \in \left( { - \infty ;0} \right] \cup \left[ {2; + \infty } \right)\)
Mà \(x \ge 0 \Rightarrow x \in \left[ {2; + \infty } \right) \cup \left\{ 0 \right\}\)
Hướng dẫn giải:
Chuyển vế, xét hàm số đặc trưng và giải bất phương trình bằng phương pháp hàm số.
Giải thích thêm:
Lưu ý điều kiện xác định của bất phương trình.
Cho khối lăng trụ tam giác đều \(ABC.{A_1}{B_1}{C_1}\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(A{A_1}\). Thể tích khối chóp \(M.BC{A_1}\) là:
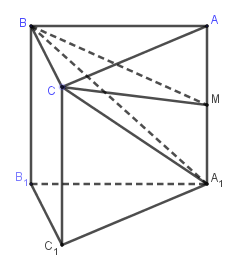
$\Delta ABC$ là tam giác đều cạnh $a$ nên có diện tích ${S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}$
Ta có $AM = \dfrac{{A{A_1}}}{2} = \dfrac{a}{2}$
Hai tứ diện $MABC$ và $M{A_1}BC$ có chung đỉnh $C$, diện tích hai đáy $MAB$ và $M{A_1}B$ bằng nhau nên có thể tích bằng nhau, suy ra
${V_{M.BC{A_1}}} = {V_{M.ABC}} = \dfrac{1}{3}AM.{S_{ABC}} = \dfrac{{{a^3}\sqrt 3 }}{{24}}$
Hướng dẫn giải:
- Chứng minh thể tích hai khối tứ diện $MABC$ và $M{A_1}BC$ có thể tích bằng nhau.
- Tính thể tích khối tứ diện $MABC$ và suy ra đáp án.
Thể tích khối bát diện đều cạnh \(a\) bằng:
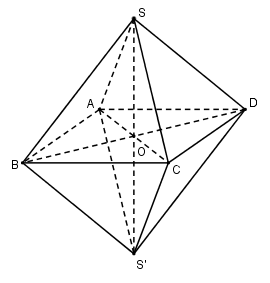
Thể tích khối bát diện đều \(V = 2{V_{S.ABCD}}\)
Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\)
Vì ABCD là hình vuông nên \(AC = BD = a\sqrt 2 \Rightarrow OA = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OA \Rightarrow \Delta SOA\) vuông tại O\( \Rightarrow SO = \sqrt {S{A^2} - O{A^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 2 }}{2}\)
\( \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}\dfrac{{a\sqrt 2 }}{2}.{a^2} = \dfrac{{{a^3}\sqrt 2 }}{6}\)
\( \Rightarrow V = 2\dfrac{{{a^3}\sqrt 2 }}{6} = \dfrac{{{a^3}\sqrt 2 }}{3}\)
Hướng dẫn giải:
- Tính thể tích mỗi khối chóp tự giác đều bởi công thức \(V = \dfrac{1}{3}Sh\).
- Tính thể tích khối bát diện đều dựa vào thể tích khối chóp đã tính.
Cho hình hộp \(ABCD.A'B'C'D'\) có thể tích bằng \(V\). Gọi \(M,\,\,N,\,\,P,\,\,Q,\,\,E,\,\,F\) lần lượt là tâm các hình bình hành \(ABCD,\,\,A'B'C'D',\,\,ABB'A',\,\,BCC'B',\,\,CDD'C',\,\,DAA'D'\). Thể tích khối đa diện có các đỉnh \(M,\,\,P,\,\,Q,\,\,E,\,\,F,\,\,N\) bằng:
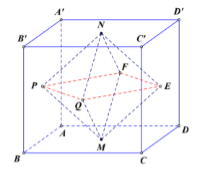
Đặc biệt hóa, coi \(ABCD.A'B'C'D'\) là khối lập phương cạnh bằng 1 \( \Rightarrow {V_{ABCD.A'B'C'D'}} = 1 = V\).
Dễ thấy \(MNPQEF\) là khối bát diện đều cạnh cạnh \(QE = \dfrac{1}{2}BD = \dfrac{{\sqrt 2 }}{2}\).
Vậy \({V_{MNPQEF}} = \dfrac{{{{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^3}\sqrt 2 }}{3} = \dfrac{1}{6} = \dfrac{V}{6}\).
Hướng dẫn giải:
Đặc biệt hóa, coi \(ABCD.A'B'C'D'\) là khối lập phương cạnh bằng .
Sử dụng công thức tính nhanh thể tích khối bát diện đều cạnh \(a\) là \(V = \dfrac{{{a^3}\sqrt 2 }}{3}\).
Cho hình nón có bán kính đáy bằng $4a$ và chiều cao bằng $3a.$ Diện tích toàn phần của hình nón bằng:
Độ dài đường sinh của hình nón $l = \sqrt {{r^2} + {h^2}} = 5a$
Diện tích xung quanh của hình nón ${S_{xq}} = \pi rl = \pi .4a.5a = 20\pi {a^2}$.
Diện tích đáy \({S_d} = \pi {r^2} = \pi {\left( {4a} \right)^2} = 16\pi {a^2}\).
Diện tích toàn phần \({S_{tp}} = {S_{xq}} + {S_d} = 20\pi {a^2} + 16\pi {a^2} = 36\pi {a^2}\)
Hướng dẫn giải:
Diện tích toàn phần của hình nón ${S_{tp}} = {S_{xq}} + {S_d} = \pi rl + \pi {r^2}$
Trong không gian \(Oxyz\), cho điểm \(A\left( {2; - 3;4} \right)\), đường thẳng \(d:\,\,\dfrac{{x - 1}}{2} = \dfrac{{y + 2}}{1} = \dfrac{z}{2}\) và mặt cầu \(\left( S \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 20\). Mặt phẳng \(\left( P \right)\) chứa đường thẳng d thỏa mãn khoảng cách từ điểm \(A\) đến \(\left( P \right)\) lớn nhất. Mặt cầu \(\left( S \right)\) cắt \(\left( P \right)\) theo đường tròn có bán kính bằng :
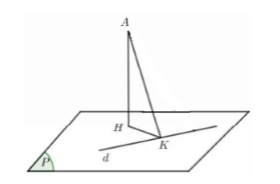
Gọi \(H,\,\,K\) lần lượt là hình chiếu của \(A\) lên \(\left( P \right)\) và \(d\) ta có \(AH \le AK\), khi đó mặt phẳng \(\left( P \right)\) chứa đường thẳng d thỏa mãn khoảng cách từ điểm \(A\) đến \(\left( P \right)\) lớn nhất \( \Leftrightarrow \left( P \right)\) nhận \(\overrightarrow {AK} \) là 1 VTPT.
Gọi \(K\left( {1 + 2t; - 2 + t;2t} \right) \in d \Rightarrow \overrightarrow {AK} = \left( {2t - 1;t + 1;2t - 4} \right)\).
\(\overrightarrow {{u_d}} \left( {2;1;2} \right)\) là 1 VTCP của \(d\).
\(\begin{array}{l} \Rightarrow \overrightarrow {AK} .\overrightarrow {{u_d}} = 0 \Leftrightarrow 4t - 2 + t + 1 + 4t - 8 = 0 \Leftrightarrow 9t - 9 = 0 \Leftrightarrow t = 1\\ \Rightarrow K\left( {3; - 1;2} \right) \Rightarrow \overrightarrow {AK} = \left( {1;2; - 2} \right)\end{array}\)
\( \Rightarrow \left( P \right):\,\,x - 3 + 2\left( {y + 1} \right) - 2\left( {z - 2} \right) = 0 \Leftrightarrow x + 2y - 2z + 3 = 0\).
Mặt cầu \(\left( S \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 20\) có tâm \(I\left( {3;2; - 1} \right)\), bán kính \(R = \sqrt {20} = 2\sqrt 5 \).
Ta có: \(d = d\left( {I;\left( P \right)} \right) = \dfrac{{\left| {3 + 2.2 - 2\left( { - 1} \right) + 3} \right|}}{{\sqrt {1 + 4 + 4} }} = \dfrac{{12}}{3} = 4\).
Gọi \(r\) là đường kính đường tròn giao tuyến của \(\left( P \right)\) và \(\left( S \right)\) ta có:
\({R^2} = {d^2} + {r^2} \Leftrightarrow r = \sqrt {{R^2} - {d^2}} = \sqrt {20 - 16} = 2\).
Hướng dẫn giải:
- Nhận xét: $d\left( {A,\left( P \right)} \right) \le d\left( {A,d} \right)$ suy ra GTLN của \(d(A,(P))\) và viết phương trình \((P)\).
- Sử dụng công thức: ${R^2} = {r^2} + {d^2}$ tính bán kính đường tròn giao tuyến.
Cho hình chóp $S.ABC$ có $SA \bot (ABC);AC = b,AB = c,\widehat {BAC} = \alpha $. Gọi $B',C'$ lần lượt là hình chiếu vuông góc của $A$ lên $SB,SC$. Tính bán kính mặt cầu ngoại tiếp khối chóp $A.{\rm{ }}BCC'B'$ theo $b,c,\alpha $
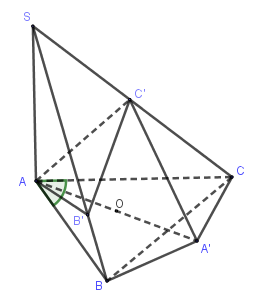
Gọi $AA'$ là đường kính của đường tròn ngoại tiếp tam giác $ABC$
\(AC \bot A'C;\,AB \bot A'B\)
Ta chứng minh \(AC' \bot A'C'\)
\(SA \bot A'C;\,AC \bot A'C \Rightarrow A'C \bot AC'\)
Mà \(AC' \bot SC \Rightarrow AC' \bot A'C'\)
Tương tự \(AB' \bot A'B'\)
Như vậy $B,C,C',B'$ cùng nhìn $AA'$ bằng $1$ góc vuông nên $A,B,C,B',C'$ cùng thuộc $1$ mặt cầu có đường kính là $AA'$ và cũng đồng thời là đường kính của đường tròn ngoại tiếp tam giác $ABC$.
Tính \(BC = \sqrt {{b^2} + {c^2} - 2b\cos \alpha } \)
Trong tam giác \(ABC:\dfrac{{BC}}{{\sin A}} = 2R \Rightarrow R = \dfrac{{\sqrt {{b^2} + {c^2} - 2bc\cos \alpha } }}{{2\sin \alpha }}\)
Hướng dẫn giải:
+ Chứng minh được tâm mặt cầu ngoại tiếp của hình chóp $ABCC'B'$ trùng với tâm đường tròn ngoại tiếp của tam giác
Tìm giá trị $m$ để phương trình \({2^{\left| {x - 1} \right| + 1}} + {2^{\left| {x - 1} \right|}} + m = 0\) có nghiệm duy nhất
Đặt \(\left| {x - 1} \right| = a\) khi đó phương trình trở thành \({2^{a + 1}} + {2^a} + m = 0\) (1)
Để phương trình đã cho có nghiệm duy nhất thì pt (1) bắt buộc phải có nghiệm duy nhất $a=0$ ( vì nếu $a>0$ thì sẽ tồn tại 2 giá trị của $x$)
Nên ${2^1} + {2^0} + m = 0$. Suy ra $m = - 3$
Hướng dẫn giải:
Chú ý đến giá trị \(a = \left| {x - 1} \right|\) .
Nếu $a > 0$ thì sẽ luôn có $2$ giá trị của $x$ nên $a$ bắt buộc phải bằng $0$.
Cho \(f\left( x \right)\) mà đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ bên
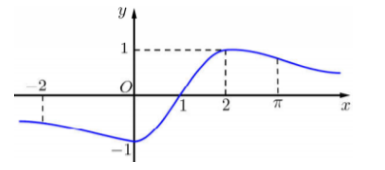
Bất phương trình \(f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m\) nghiệm đúng với mọi \(x \in \left[ { - 1;3} \right]\) khi và chỉ khi:
\(\begin{array}{l}f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m\,\,\forall x \in \left[ { - 1;3} \right] \Leftrightarrow g\left( x \right) = f\left( x \right) - \sin \dfrac{{\pi x}}{2} > m\,\,\forall x \in \left[ { - 1;3} \right]\\ \Rightarrow m < \mathop {\min }\limits_{\left[ { - 1;3} \right]} g\left( x \right)\end{array}\).
Từ đồ thị hàm số \(y = f'\left( x \right)\) ta suy ra BBT đồ thị hàm số \(y = f\left( x \right)\) như sau:
Dựa vào BBT ta thấy \(f\left( x \right) \ge f\left( 1 \right)\,\,\forall x \in \left[ { - 1;3} \right]\).
\(\begin{array}{l}x \in \left[ { - 1;3} \right] \Rightarrow \dfrac{{\pi x}}{2} \in \left[ { - \dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right] \Rightarrow - 1 \le \sin \dfrac{{\pi x}}{2} \le 1\\ \Leftrightarrow - 1 \le - \sin \dfrac{{\pi x}}{2} \le 1\end{array}\)
\( \Rightarrow f\left( 1 \right) - 1 \le f\left( x \right) - \sin \dfrac{{\pi x}}{2} \Leftrightarrow g\left( x \right) \ge f\left( 1 \right) - 1 \Rightarrow \mathop {\min }\limits_{\left[ { - 1;3} \right]} g\left( x \right) = f\left( 1 \right) - 1\).
Vậy \(m < f\left( 1 \right) - 1\).
Hướng dẫn giải:
- Biến đổi bất phương trình về dạng \(g(x)>m\).
- Xét hàm \(y=g(x)\) và tìm GTNN của \(g(x)\).
- Bài toán thỏa khi \(m<\mathop {\min }\limits_{\left[ { - 1;3} \right]} g\left( x \right)\)
Cho khối đa diện có các mặt đều là tam giác, kí hiệu số mặt là \(M\), số cạnh là \(C\). Chọn mệnh đề đúng:
Vì mỗi mặt là tam giác nên mỗi mặt có \(3\) cạnh
Do đó M mặt sẽ có \(3M\) cạnh hay đa diện có 3M cạnh.
Tuy nhiên, mỗi cạnh lại là cạnh chung của \(2\) mặt nên mỗi cạnh trên đã được đếm 2 lần.
Số cạnh thực tế của đa diện chỉ là \(C = \frac{{3M}}{2}\) hay \(2C = 3M\).
Giải thích thêm:
Một số em có thể chọn nhầm đáp án B vì nhớ nhầm công thức.
Cho hình chóp đều $n$ cạnh $(n \ge 3)$. Cho biết bán kính đường tròn ngoại tiếp đa giác đáy là $R$ và góc giữa mặt bên và mặt đáy bằng ${60^0}$ , thể tích khối chóp bằng $\dfrac{{3\sqrt 3 }}{4}{R^3}$ . Tìm $n$?
Giả sử đáy là đa giác đều ${A_1}{A_2}...{A_n}$. $O$ là tâm đáy, chóp có chiều cao là $SH$ . Gọi $I$ là trung điểm của ${A_1}{A_2}$
Ta có : $I{A_1} = R.\sin \dfrac{\pi }{n};OI = R.\cos \dfrac{\pi }{n}$
$SO = OI.\tan {60^0} = R.\cos \dfrac{\pi }{n}.\sqrt 3 = R\sqrt 3 .\cos \dfrac{\pi }{n}$
Diện tích đáy : $S = \dfrac{{3V}}{{SO}} = \dfrac{{3.\dfrac{{3\sqrt 3 }}{4}.{R^3}}}{{R\sqrt 3 .cos\dfrac{\pi }{n}}} = \dfrac{{9{R^2}}}{{4\cos \dfrac{\pi }{n}}}$
Mà $S = n.\dfrac{1}{2}{R^2}.\sin \dfrac{{2\pi }}{n} \Rightarrow \dfrac{{9{R^2}}}{{4\cos \dfrac{\pi }{n}}} = n.\dfrac{1}{2}.{R^2}.\sin \dfrac{{2\pi }}{n}$
$ \Leftrightarrow n\sin \dfrac{{2\pi }}{n}\cos \dfrac{\pi }{n} = \dfrac{9}{2}$
Thử các giá trị của $n$ ở các đáp án ta được \(n = 6\).
Hướng dẫn giải:
- Gọi $I$ là trung điểm của ${A_1}{A_2}$.
- Tính \(SO \Rightarrow \) diện tích đa giác đáy.
- Viết công thức tính diện tích đa giác đáy theo \(n\) rồi thử đáp án.
Cho hàm số $y = {x^3} - 3{x^2} + 2x - 5$ có đồ thị $\left( C \right)$. Có bao nhiêu cặp điểm thuộc đồ thị $\left( C \right)$ mà tiếp tuyến với đồ thị tại chúng là hai đường thẳng song song?
Ta có: $y' = 3{{\text{x}}^2} - 6{\text{x}} + 2$
Số cặp điểm thuộc đồ thị $\left( C \right)$ có tiếp tuyến song song nhau
$ \Leftrightarrow $ số cặp nghiệm phương trình $3{{\text{x}}^2} - 6{\text{x}} + 2 = m$ với $m \in R$ thỏa mãn phương trình $3{x^2} - 6x + 2 = m$ có hai nghiệm phân biệt.Có vô số giá trị của $m$ để phương trình trên có hai nghiệm phân biệt nên có vô số cặp điểm.
Hướng dẫn giải:
Gọi hệ số góc của hai tiếp tuyến song song là $m$, khi đó số cặp điểm thỏa mãn chính là số cặp nghiệm của phương trình $y' = m$ với $m$ bất kì.
Giải thích thêm:
Có thể sử dụng nhận xét dưới đây:
Các tiếp tuyến với đồ thị hàm số bậc ba tại hai tiếp điểm mà đối xứng với nhau qua điểm uốn thì đều song song.
Do đó có vô số cặp điểm thuộc đồ thị hàm số mà đối xứng với nhau qua điểm uốn nên sẽ có vô số cặp điểm thỏa mãn bài toán.
Đề thi liên quan
-
Đề kiểm tra học kì 1 - Đề số 2
-
50 câu hỏi
-
90 phút
-
-
Đề kiểm tra học kì 1 - Đề số 3
-
50 câu hỏi
-
90 phút
-
-
Đề kiểm tra học kì 1 - Đề số 4
-
50 câu hỏi
-
90 phút
-
-
Đề kiểm tra học kì 1 - Đề số 5
-
50 câu hỏi
-
90 phút
-

