Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác cân tại \(A\), biết \(SA \bot \left( {ABC} \right)\), \(BC = 2a,\widehat {BAC} = {120^0}\), góc giữa mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) bằng \({45^0}\). Tính thể tích khối chóp \(S.ABC\).
A.
\(\dfrac{{{a^3}}}{2}\)
B.
\(\dfrac{{{a^3}}}{9}\)
C.
\({a^3}\sqrt 2 \)
D.
\(\dfrac{{{a^3}}}{3}\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: b
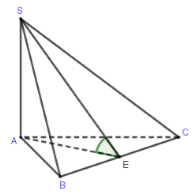
Gọi \(E\) là trung điểm của \(BC\) \( \Rightarrow \left\{ \begin{array}{l}AE \bot BC\\SA \bot BC\end{array} \right. \Rightarrow BC \bot \left( {SAE} \right) \Rightarrow BC \bot SE\)
Ta có: \(\left\{ \begin{array}{l}AE \bot BC\\SE \bot BC\\\left( {ABC} \right) \cap \left( {SBC} \right) = BC\end{array} \right. \Rightarrow \angle \left( {\left( {ABC} \right);\left( {SBC} \right)} \right) = \angle SEA = {45^0}.\)
\( \Rightarrow \Delta SAE\) vuông cân tại \(A \Rightarrow SA = AE\).
Tam giác \(ABC\) cân tại \(A\) có \(\widehat A = {120^0},BC = 2a\),
\(AE\) là tia phân giác của \(\widehat A\) \( \Rightarrow \widehat {BAE} = {60^0}\).
Tam giác vuông \(AEB\) có \(\widehat {BAE} = {60^0},BE = \dfrac{1}{2}BC = a \Rightarrow AE = \dfrac{{BE}}{{\tan {{60}^0}}} = \dfrac{{BE}}{{\sqrt 3 }} = \dfrac{{a\sqrt 3 }}{3} = SA\).
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}.SA.\dfrac{1}{2}AE.BC = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{3}.\dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{3}.2a = \dfrac{{{a^3}}}{9}\).
Hướng dẫn giải:
- Xác định góc giữa hai mặt phẳng: là góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến.
- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao.

Gọi \(E\) là trung điểm của \(BC\) \( \Rightarrow \left\{ \begin{array}{l}AE \bot BC\\SA \bot BC\end{array} \right. \Rightarrow BC \bot \left( {SAE} \right) \Rightarrow BC \bot SE\)
Ta có: \(\left\{ \begin{array}{l}AE \bot BC\\SE \bot BC\\\left( {ABC} \right) \cap \left( {SBC} \right) = BC\end{array} \right. \Rightarrow \angle \left( {\left( {ABC} \right);\left( {SBC} \right)} \right) = \angle SEA = {45^0}.\)
\( \Rightarrow \Delta SAE\) vuông cân tại \(A \Rightarrow SA = AE\).
Tam giác \(ABC\) cân tại \(A\) có \(\widehat A = {120^0},BC = 2a\),
\(AE\) là tia phân giác của \(\widehat A\) \( \Rightarrow \widehat {BAE} = {60^0}\).
Tam giác vuông \(AEB\) có \(\widehat {BAE} = {60^0},BE = \dfrac{1}{2}BC = a \Rightarrow AE = \dfrac{{BE}}{{\tan {{60}^0}}} = \dfrac{{BE}}{{\sqrt 3 }} = \dfrac{{a\sqrt 3 }}{3} = SA\).
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}.SA.\dfrac{1}{2}AE.BC = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{3}.\dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{3}.2a = \dfrac{{{a^3}}}{9}\).
Hướng dẫn giải:
- Xác định góc giữa hai mặt phẳng: là góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến.
- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao.
CÂU HỎI CÙNG CHỦ ĐỀ
Tìm giá trị $m$ để phương trình \({2^{\left| {x - 1} \right| + 1}} + {2^{\left| {x - 1} \right|}} + m = 0\) có nghiệm duy nhất
Biết rằng hàm số \(f\left( x \right) = \sqrt x \ln x\) đạt giá trị lớn nhất trên đoạn \(\left[ {1;e} \right]\) tại \(x = {x_0}\). Mệnh đề nào sau đây là đúng?
Công thức tính thể tích khối nón có bán kính đáy \(r\), độ dài đường sinh \(l\) và chiều cao \(h\) là:
Trong không gian \(Oxyz\), cho điểm \(A\left( {2; - 3;4} \right)\), đường thẳng \(d:\,\,\dfrac{{x - 1}}{2} = \dfrac{{y + 2}}{1} = \dfrac{z}{2}\) và mặt cầu \(\left( S \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 20\). Mặt phẳng \(\left( P \right)\) chứa đường thẳng d thỏa mãn khoảng cách từ điểm \(A\) đến \(\left( P \right)\) lớn nhất. Mặt cầu \(\left( S \right)\) cắt \(\left( P \right)\) theo đường tròn có bán kính bằng :
Tìm tất cả các giá trị thực của $m$ để hàm số $y = {x^4} + 2\left( {{m^2} - 9} \right){x^2} + 5m + 2$ có cực đại, cực tiểu
Cho khối lăng trụ tam giác đều \(ABC.{A_1}{B_1}{C_1}\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(A{A_1}\). Thể tích khối chóp \(M.BC{A_1}\) là:
Cho hình nón có bán kính đáy bằng $4a$ và chiều cao bằng $3a.$ Diện tích toàn phần của hình nón bằng:
Cho hàm số \(y = f\left( x \right)\) xác định và có đạo hàm \(f'\left( x \right) = {x^2} + 2\) trên \(R\), chọn kết luận đúng:
Cho hàm số $y = {x^4} - 2(m + 1){x^2} + m + 2$ có đồ thị $\left( C \right)$. Gọi $\Delta $ là tiếp tuyến với đồ thị $\left( C \right)$ tại điểm thuộc $\left( C \right)$ có hoành độ bằng $1$. Với giá trị nào của tham số $m$ thì $\Delta $ vuông góc với đường thẳng $d:y = - \dfrac{1}{4}x - 2016$
Cho khối nón có độ dài đường sinh bằng \(2a\) và bán kính đáy bằng \(a\). Thể tích của khối nón đã cho bằng
Cho hàm số \(y = f\left( x \right)\) có hai giá trị cực đại, cực tiểu thỏa mãn \({y_{CD}}.{y_{CT}} = 0\). Khi đó:
Điều kiện để biểu thức \({\log _2}\left( {3 - x} \right)\) xác định là:
Nếu $\mathop {\lim }\limits_{x \to x_0^ + } y = + \infty $ thì đường thẳng $x = {x_0}$ là:
Cho hình chóp đều $n$ cạnh $(n \ge 3)$. Cho biết bán kính đường tròn ngoại tiếp đa giác đáy là $R$ và góc giữa mặt bên và mặt đáy bằng ${60^0}$ , thể tích khối chóp bằng $\dfrac{{3\sqrt 3 }}{4}{R^3}$ . Tìm $n$?
Tập nghiệm của bất phương trình \({3^{\sqrt {2x} + 1}} - {3^{x + 1}} \le {x^2} - 2x\) là:

