Trong không gian \(Oxyz\), cho điểm \(A\left( {2; - 3;4} \right)\), đường thẳng \(d:\,\,\dfrac{{x - 1}}{2} = \dfrac{{y + 2}}{1} = \dfrac{z}{2}\) và mặt cầu \(\left( S \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 20\). Mặt phẳng \(\left( P \right)\) chứa đường thẳng d thỏa mãn khoảng cách từ điểm \(A\) đến \(\left( P \right)\) lớn nhất. Mặt cầu \(\left( S \right)\) cắt \(\left( P \right)\) theo đường tròn có bán kính bằng :

Đáp án đúng: d

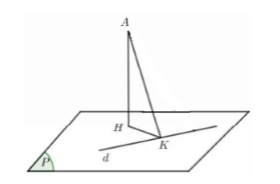
Gọi \(H,\,\,K\) lần lượt là hình chiếu của \(A\) lên \(\left( P \right)\) và \(d\) ta có \(AH \le AK\), khi đó mặt phẳng \(\left( P \right)\) chứa đường thẳng d thỏa mãn khoảng cách từ điểm \(A\) đến \(\left( P \right)\) lớn nhất \( \Leftrightarrow \left( P \right)\) nhận \(\overrightarrow {AK} \) là 1 VTPT.

Gọi \(K\left( {1 + 2t; - 2 + t;2t} \right) \in d \Rightarrow \overrightarrow {AK}  = \left( {2t - 1;t + 1;2t - 4} \right)\).

\(\overrightarrow {{u_d}} \left( {2;1;2} \right)\) là 1 VTCP của \(d\).

\(\begin{array}{l} \Rightarrow \overrightarrow {AK} .\overrightarrow {{u_d}}  = 0 \Leftrightarrow 4t - 2 + t + 1 + 4t - 8 = 0 \Leftrightarrow 9t - 9 = 0 \Leftrightarrow t = 1\\ \Rightarrow K\left( {3; - 1;2} \right) \Rightarrow \overrightarrow {AK}  = \left( {1;2; - 2} \right)\end{array}\)

\( \Rightarrow \left( P \right):\,\,x - 3 + 2\left( {y + 1} \right) - 2\left( {z - 2} \right) = 0 \Leftrightarrow x + 2y - 2z + 3 = 0\).

Mặt cầu \(\left( S \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 20\) có tâm \(I\left( {3;2; - 1} \right)\), bán kính \(R = \sqrt {20}  = 2\sqrt 5 \).

Ta có: \(d = d\left( {I;\left( P \right)} \right) = \dfrac{{\left| {3 + 2.2 - 2\left( { - 1} \right) + 3} \right|}}{{\sqrt {1 + 4 + 4} }} = \dfrac{{12}}{3} = 4\).

Gọi \(r\) là đường kính đường tròn giao tuyến của \(\left( P \right)\) và \(\left( S \right)\) ta có:

\({R^2} = {d^2} + {r^2} \Leftrightarrow r = \sqrt {{R^2} - {d^2}}  = \sqrt {20 - 16}  = 2\).

Hướng dẫn giải:

- Nhận xét: $d\left( {A,\left( P \right)} \right) \le d\left( {A,d} \right)$ suy ra GTLN của \(d(A,(P))\) và viết phương trình \((P)\).

- Sử dụng công thức: ${R^2} = {r^2} + {d^2}$ tính bán kính đường tròn giao tuyến.