Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
Hỏi bàiĐề kiểm tra 15 phút chương 2: Hàm số lũy thừa, mũ, logarit - Đề số 1
-
Hocon247
-
12 câu hỏi
-
45 phút
-
588 lượt thi
-
Dễ
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Kết luận nào đúng về số thực \(a\) nếu \({\left( {\dfrac{1}{a}} \right)^{ - 0,2}} < {a^2}\)
\({\left( {\dfrac{1}{a}} \right)^{ - 0,2}} < {a^2} \Leftrightarrow {a^{0,2}} < {a^2}\)
Do \(0,2 < 2\) và có số mũ không nguyên nên ${a^{0,2}} < {a^2}$ khi $a > 1$.
Hướng dẫn giải:
Sử dụng so sánh lũy thừa:
+ Với \(a > 1\) thì \({a^m} > {a^n} \Leftrightarrow m > n\)
+ Với \(0 < a < 1\) thì \({a^m} > {a^n} \Leftrightarrow m < n\)
Nếu $n$ chẵn thì điều kiện để $\sqrt[n]{b}$ có nghĩa là:
Với $n$ chẵn thì $\sqrt[n]{b}$ tồn tại nếu $b \ge 0$.
Với điều kiện các biểu thức đều có nghĩa, đẳng thức nào dưới đây không đúng?
Ta có:
${\log _a}{b^n} = n{\log _a}b\left( {0 < a \ne 1;b > 0} \right)$
${\log _a}\dfrac{1}{b} = - {\log _a}b\left( {0 < a \ne 1;b > 0} \right)$
${\log _a}\sqrt[n]{b} = {\log _a}{b^{\dfrac{1}{n}}} = \dfrac{1}{n}{\log _a}b\left( {0 < a \ne 1;b > 0;n > 0;n \in {N^*}} \right)$
Vậy đẳng thức không đúng là ${\log _a}\sqrt[n]{b} = - n{\log _a}b$.
Hướng dẫn giải:
Sử dụng các công thức biến đổi logarit:
${\log _a}{b^n} = n{\log _a}b\left( {0 < a \ne 1;b > 0} \right)$
${\log _a}\dfrac{1}{b} = - {\log _a}b\left( {0 < a \ne 1;b > 0} \right)$
${\log _a}\sqrt[n]{b} = {\log _a}{b^{\dfrac{1}{n}}} = \dfrac{1}{n}{\log _a}b\left( {0 < a \ne 1;b > 0;n > 0;n \in {N^*}} \right)$
Chọn mệnh đề đúng:
Ta có: ${\log _2}16 = {\log _2}{2^4} = 4$; ${\log _3}81 = {\log _3}{3^4} = 4$ nên ${\log _2}16 = {\log _3}81$.
Hướng dẫn giải:
Sử dụng công thức ${\log _a}{a^b} = b$ với $0<a\ne 1$.
Giải thích thêm:
HS sẽ chọn nhầm các đáp án B, C, D vì nghĩ rằng ${\log _3}9 = 9:3 = 3$ là sai.
Chọn mệnh đề đúng:
Ta có: \(\ln \left( {ab} \right) = \ln a + \ln b\) nên A sai.
\(\ln \left( {\dfrac{a}{b}} \right) = \ln a - \ln b\) nên B sai.
\(\ln {a^n} = n\ln a\left( {a > 0} \right)\) nên C đúng.
\(\ln e = 1\) nên D sai.
Công thức nào sau đây là công thức tăng trưởng mũ?
Công thức lãi kép (hoặc công thức tăng trưởng mũ):
\(T = A.{e^{Nr}}\), ở đó \(A\) là số tiền gửi ban đầu, \(r\) là lãi suất, \(N\) là số kì hạn.
Cho hàm số \(y = {x^\alpha }\). Nếu \(\alpha = 1\) thì đồ thị hàm số là:
Với \(\alpha = 1\) thì \(y = {x^1} = x\) nên đồ thị hàm số là đường thẳng.
Cho ${\left( {\sqrt 2 - 1} \right)^m} < {\left( {\sqrt 2 - 1} \right)^n}$. Khẳng định nào dưới đây đúng?
Vì $0 < \sqrt 2 - 1 < 1$ nên ${\left( {\sqrt 2 - 1} \right)^m} < {\left( {\sqrt 2 - 1} \right)^n} \Leftrightarrow m > n$.
Hướng dẫn giải:
Sử dụng tính chất so sánh: Với $0 < a < 1$ thì ${a^m} > {a^n} \Leftrightarrow m < n$.
Giải thích thêm:
HS thường chọn nhầm đáp án A khi không để ý đến điều kiện $0 < \sqrt 2 - 1 < 1$.
Đơn giản biểu thức $P = \left( {{a^{\dfrac{1}{4}}} - {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{4}}} + {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{2}}} + {b^{\dfrac{1}{2}}}} \right)\,\,\,\,(a,b > 0)$ ta được:
Ta có:
$P = \left( {{a^{\dfrac{1}{4}}} - {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{4}}} + {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{2}}} + {b^{\dfrac{1}{2}}}} \right) = \left( {{a^{\dfrac{1}{2}}} - {b^{\dfrac{1}{2}}}} \right)\left( {{a^{\dfrac{1}{2}}} + {b^{\dfrac{1}{2}}}} \right) = a - b$
Vậy \(P = a - b\).
Hướng dẫn giải:
Sử dụng các công thức lũy thừa với số mũ hữu tỉ \({a^m}.{a^n} = {a^{m + n}}\).
Giải thích thêm:
HS cần chú ý, tránh sử dụng nhầm công thức \({a^m}.{a^n} = {a^{mn}}\) sẽ dẫn đến chọn nhầm đáp án .
Các em cũng có thể thực hiện phép nhân bằng việc sử dụng hằng đẳng thức $a^2-b^2=(a-b)(a+b)$
Cho \(a\) là số thực tùy ý và \(b,c\) là các số thực dương khác \(1\). Hình vẽ bên là đồ thị của ba hàm số \(y = {\log _b}x;y = {\log _c}x;y = {x^a}\left( {x > 0} \right)\). Khẳng định nào sau đây đúng?
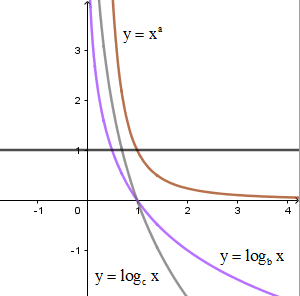
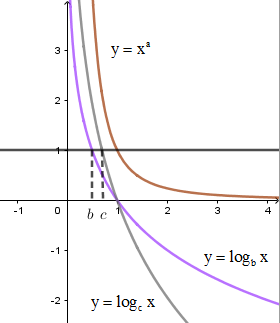
Ta thấy hàm số \(y = {x^a}\) nghịch biến nên \(a < 0\) nên loại C, D.
Kẻ đường thẳng \(y = 1\) cắt hai đồ thị hàm số \(y = {\log _b}x;y = {\log _c}x\) tại hai điểm lần lượt có hoành độ \(x = b;x = c\). Quan sát đồ thị ta thấy \(b < c\).
Vậy \(a < b < c\).
Hướng dẫn giải:
Quan sát các đồ thị hàm số và nhận xét.
Giải thích thêm:
HS sẽ nhầm lẫn ở việc nhận dạng: Nhiều em sẽ nhận xét đồ thị hàm số \(y = {x^a}\) nằm ở phía trên cả hai đồ thị hàm số \(y = {\log _b}x;y = {\log _c}x\) nên kết luận ngay \(a > b,c\) nên chọn sai đáp án.
Một khu rừng ở tỉnh Hà Giang có trữ lượng gỗ là $3.10^5(m^3).$ Biết tốc độ sinh trưởng của các ở khu rừng đó là $5\%$ mỗi năm. Hỏi sau $5$ năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ?
Trữ lượng gỗ sau năm thứ nhất: ${3.10}^5.(1+0,05)$
Trữ lượng gỗ sau năm thứ 2: ${3.10}^5.(1+0,05).+{3.10}^5.(1+0,05).0,05={3.10}^5.{(1+0,05)}^2$
Tương tự như vậy đến năm thứ 5 trữ lượng gỗ ở khu rừng đó là : ${3.10}^5.{(1+0,05)}^5$
Hướng dẫn giải:
Sử dụng công thức lãi kép $T = A{\left( {1 + r} \right)^N}$
Nếu $\log_a b{\rm{ }} = {\rm{ }}p$ thì $\log_a{a^2}{b^4}$ bằng:
Ta có: $\log_a{a^2}{b^4} = \log_a{a^2} + \log_a{b^4} $ $= 2\log_a a + 4\log_a b = 2 + 4p$
Hướng dẫn giải:
Lần lượt áp dụng các công thức:
${\log _a}xy = {\log _a}x + {\log _a}y$
${\log _a}{b^n} = n{\log _a}b$
${\log _a}a = 1$
