Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: d
Ta có:
${\log _a}{b^n} = n{\log _a}b\left( {0 < a \ne 1;b > 0} \right)$
${\log _a}\dfrac{1}{b} = - {\log _a}b\left( {0 < a \ne 1;b > 0} \right)$
${\log _a}\sqrt[n]{b} = {\log _a}{b^{\dfrac{1}{n}}} = \dfrac{1}{n}{\log _a}b\left( {0 < a \ne 1;b > 0;n > 0;n \in {N^*}} \right)$
Vậy đẳng thức không đúng là ${\log _a}\sqrt[n]{b} = - n{\log _a}b$.
Hướng dẫn giải:
Sử dụng các công thức biến đổi logarit:
${\log _a}{b^n} = n{\log _a}b\left( {0 < a \ne 1;b > 0} \right)$
${\log _a}\dfrac{1}{b} = - {\log _a}b\left( {0 < a \ne 1;b > 0} \right)$
${\log _a}\sqrt[n]{b} = {\log _a}{b^{\dfrac{1}{n}}} = \dfrac{1}{n}{\log _a}b\left( {0 < a \ne 1;b > 0;n > 0;n \in {N^*}} \right)$
Ta có:
${\log _a}{b^n} = n{\log _a}b\left( {0 < a \ne 1;b > 0} \right)$
${\log _a}\dfrac{1}{b} = - {\log _a}b\left( {0 < a \ne 1;b > 0} \right)$
${\log _a}\sqrt[n]{b} = {\log _a}{b^{\dfrac{1}{n}}} = \dfrac{1}{n}{\log _a}b\left( {0 < a \ne 1;b > 0;n > 0;n \in {N^*}} \right)$
Vậy đẳng thức không đúng là ${\log _a}\sqrt[n]{b} = - n{\log _a}b$.
Hướng dẫn giải:
Sử dụng các công thức biến đổi logarit:
${\log _a}{b^n} = n{\log _a}b\left( {0 < a \ne 1;b > 0} \right)$
${\log _a}\dfrac{1}{b} = - {\log _a}b\left( {0 < a \ne 1;b > 0} \right)$
${\log _a}\sqrt[n]{b} = {\log _a}{b^{\dfrac{1}{n}}} = \dfrac{1}{n}{\log _a}b\left( {0 < a \ne 1;b > 0;n > 0;n \in {N^*}} \right)$
CÂU HỎI CÙNG CHỦ ĐỀ
Nếu $n$ chẵn thì điều kiện để $\sqrt[n]{b}$ có nghĩa là:
Kết luận nào đúng về số thực \(a\) nếu \({\left( {\dfrac{1}{a}} \right)^{ - 0,2}} < {a^2}\)
Cho hàm số \(y = {x^\alpha }\). Nếu \(\alpha = 1\) thì đồ thị hàm số là:
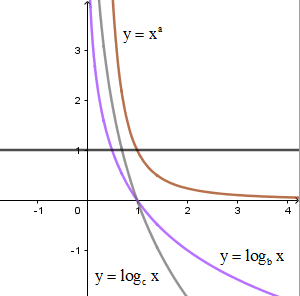
Cho \(a\) là số thực tùy ý và \(b,c\) là các số thực dương khác \(1\). Hình vẽ bên là đồ thị của ba hàm số \(y = {\log _b}x;y = {\log _c}x;y = {x^a}\left( {x > 0} \right)\). Khẳng định nào sau đây đúng?
Đơn giản biểu thức $P = \left( {{a^{\dfrac{1}{4}}} - {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{4}}} + {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{2}}} + {b^{\dfrac{1}{2}}}} \right)\,\,\,\,(a,b > 0)$ ta được:
Nếu $\log_a b{\rm{ }} = {\rm{ }}p$ thì $\log_a{a^2}{b^4}$ bằng:
Cho ${\left( {\sqrt 2 - 1} \right)^m} < {\left( {\sqrt 2 - 1} \right)^n}$. Khẳng định nào dưới đây đúng?
Công thức nào sau đây là công thức tăng trưởng mũ?
Một khu rừng ở tỉnh Hà Giang có trữ lượng gỗ là $3.10^5(m^3).$ Biết tốc độ sinh trưởng của các ở khu rừng đó là $5\%$ mỗi năm. Hỏi sau $5$ năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ?

