Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: a
Ta có: ${\log _2}16 = {\log _2}{2^4} = 4$; ${\log _3}81 = {\log _3}{3^4} = 4$ nên ${\log _2}16 = {\log _3}81$.
Hướng dẫn giải:
Sử dụng công thức ${\log _a}{a^b} = b$ với $0<a\ne 1$.
Giải thích thêm:
HS sẽ chọn nhầm các đáp án B, C, D vì nghĩ rằng ${\log _3}9 = 9:3 = 3$ là sai.
Ta có: ${\log _2}16 = {\log _2}{2^4} = 4$; ${\log _3}81 = {\log _3}{3^4} = 4$ nên ${\log _2}16 = {\log _3}81$.
Hướng dẫn giải:
Sử dụng công thức ${\log _a}{a^b} = b$ với $0<a\ne 1$.
Giải thích thêm:
HS sẽ chọn nhầm các đáp án B, C, D vì nghĩ rằng ${\log _3}9 = 9:3 = 3$ là sai.
CÂU HỎI CÙNG CHỦ ĐỀ
Nếu $n$ chẵn thì điều kiện để $\sqrt[n]{b}$ có nghĩa là:
Kết luận nào đúng về số thực \(a\) nếu \({\left( {\dfrac{1}{a}} \right)^{ - 0,2}} < {a^2}\)
Cho hàm số \(y = {x^\alpha }\). Nếu \(\alpha = 1\) thì đồ thị hàm số là:
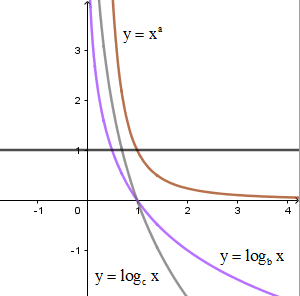
Cho \(a\) là số thực tùy ý và \(b,c\) là các số thực dương khác \(1\). Hình vẽ bên là đồ thị của ba hàm số \(y = {\log _b}x;y = {\log _c}x;y = {x^a}\left( {x > 0} \right)\). Khẳng định nào sau đây đúng?
Đơn giản biểu thức $P = \left( {{a^{\dfrac{1}{4}}} - {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{4}}} + {b^{\dfrac{1}{4}}}} \right)\left( {{a^{\dfrac{1}{2}}} + {b^{\dfrac{1}{2}}}} \right)\,\,\,\,(a,b > 0)$ ta được:
Nếu $\log_a b{\rm{ }} = {\rm{ }}p$ thì $\log_a{a^2}{b^4}$ bằng:
Cho ${\left( {\sqrt 2 - 1} \right)^m} < {\left( {\sqrt 2 - 1} \right)^n}$. Khẳng định nào dưới đây đúng?
Với điều kiện các biểu thức đều có nghĩa, đẳng thức nào dưới đây không đúng?
Công thức nào sau đây là công thức tăng trưởng mũ?
Một khu rừng ở tỉnh Hà Giang có trữ lượng gỗ là $3.10^5(m^3).$ Biết tốc độ sinh trưởng của các ở khu rừng đó là $5\%$ mỗi năm. Hỏi sau $5$ năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ?

