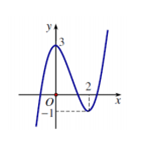
A sai vì $y=3$ là giá trị cực đại của hàm số, không phải giá trị lớn nhất.

B sai vì hàm số đồng biến trên các khoảng $\left( { - \infty ;0} \right),\left( {2; + \infty } \right)$.

C sai vì $x=2$ là điểm cực tiểu của hàm số không phải giá trị cực tiểu.

D đúng vì trên đoạn $\left[ {0;4} \right]$ thì hàm số đạt GTNN (cũng là giá trị cực tiểu) bằng $- 1$ đạt được tại $x = 2$.

Nếu $f'\left( x \right)$ đổi dấu từ âm sang dương qua điểm ${x_0}$ thì ${x_0}$ là điểm cực tiểu của hàm số.

GTNN của $f\left( x \right)$ trên $\left[ {0;2} \right]$ bằng $5$ nên $f\left( x \right) \geqslant 5,\forall x \in \left[ {0;2} \right] \Rightarrow f\left( 2 \right) \geqslant 5$.

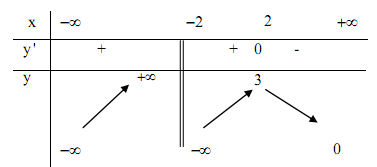
Từ bảng biến thiên ta thấy: 

Đạo hàm đổi dấu từ dương sang âm qua điểm $x = 2$ nên $x = 2$ là điểm cực đại của hàm số, $y = 3$ là giá trị cực đại của hàm số và $\left( {2;3} \right)$ là điểm cực đại của đồ thị hàm số.

Ngoài ra, đạo hàm không đổi dấu qua điểm $x =  - 2$ nên $x =  - 2$ không là điểm cực trị của hàm số.

TXĐ $D = \mathbb{R}$

$y' =  - {x^2} + \dfrac{2}{3}mx \Rightarrow y'' =  - 2x + \dfrac{2}{3}m$

Hàm số đã cho đạt cực đại tại $x = 2$

$\Leftrightarrow \left\{ \begin{gathered}  y'(2) = 0 \hfill \\ y''\left( 2 \right) < 0 \hfill \\ \end{gathered}  \right.$ $\Leftrightarrow \left\{ \begin{gathered} - {2^2} + \dfrac{2}{3}m.2 = 0 \hfill \\ - 2.2 + \dfrac{2}{3}m. < 0 \hfill \\ \end{gathered}  \right.$ $\Leftrightarrow \left\{ \begin{gathered} - 4 + \dfrac{4}{3}m = 0 \hfill \\- 4 + \dfrac{2}{3}m < 0 \hfill \\ \end{gathered}  \right.$ $\Leftrightarrow \left\{ \begin{gathered} m = 3 \hfill \\m < 6 \hfill \\ \end{gathered}  \right. \Leftrightarrow m = 3$

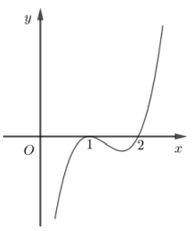
Hàm số $y = f'\left( x \right)$ dương trong khoảng $\left( {2; + \infty } \right)$

$\Rightarrow$  Hàm số $y = f\left( x \right)$ đồng biến trên $\left( {2; + \infty } \right)$

+) Xét đáp án A:$y = \sin x - 3x$ có: $y' = \cos x - 3.$

Với $\forall {\mkern 1mu} {\mkern 1mu} x \in R$ ta có: $- 1 \le \cos x \le 1 \Rightarrow y' = {\rm{cosx\;}} - 3 < 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \forall x{\mkern 1mu} {\mkern 1mu}  \in R \Rightarrow$ hàm số nghịch biến trên $R.$

Vậy hàm số ở đáp án A không đồng biến trên $R$.

+) Xét đáp án B: $y = \cos x + 2x$ có: $y' = {\rm{\;}} - \sin x + 2.$

Với $\forall {\mkern 1mu} {\mkern 1mu} x \in R$ ta có: $- 1 \le \sin x \le 1 \Rightarrow y' = {\rm{\;}} - \sin x + 2 > 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \forall x{\mkern 1mu} {\mkern 1mu}  \in R$

Vậy hàm số đồng biến trên $\mathbb{R}.$

+) Xét đáp án C: $y'=3x^2\ge 0, \forall x$ nên hàm số đồng biến trên $R$.

+) Xét đáp án D: $y'=5x^4\ge 0, \forall x$ nên hàm số đồng biến trên $R$.

Vậy chỉ có hàm số ở đáp án A không đồng biến trên $R$.

Hàm số bậc ba chỉ có thể có $2$ cực trị hoặc không có cực trị nào nên nếu nó có cực đại thì chắc chắn sẽ có cực tiểu và ngược lại nên A, B sai.

Không phải lúc nào hàm bậc ba cũng có $2$ cực trị, vẫn có trường hợp không có cực trị nên D sai.

Ta có: $y' = {x^2} - 4mx + 4m$.

Hàm số nghịch biến trên $\left( { - 2;0} \right) \Rightarrow y' \leqslant 0,\forall x \in \left( { - 2;0} \right) \Leftrightarrow {x^2} - 4mx + 4m \leqslant 0,\forall x \in \left( { - 2;0} \right)$ $\Leftrightarrow {x^2} - 4m\left( {x - 1} \right) \leqslant 0 \Leftrightarrow 4m\left( {x - 1} \right) \geqslant {x^2} \Leftrightarrow 4m \leqslant \dfrac{{{x^2}}}{{x- 1}}$ (vì $- 2 < x < 0$)

Xét hàm $g\left( x \right) = \dfrac{{{x^2}}}{{x - 1}}$ trên $\left( { - 2;0} \right)$ ta có:

$g'\left( x \right) = \dfrac{{{x^2} - 2x}}{{{{\left( {x - 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{gathered}x = 0 \notin \left( { - 2;0} \right) \hfill \\x = 2 \notin \left( { - 2;0} \right) \hfill \\ \end{gathered}  \right. \Rightarrow g'\left( x \right) > 0,\forall x \in \left( { - 2;0} \right)$

Do đó hàm số $y = g\left( x \right)$ đồng biến trên $\left( { - 2;0} \right)$

Suy ra $g\left( { - 2} \right) < g\left( x \right) < g\left( 0 \right),\forall x \in \left( { - 2;0} \right)$ hay $- \dfrac{4}{3} < g\left( x \right) < 0,\forall x \in \left( { - 2;0} \right)$

Khi đó $4m \le g\left( x \right),\forall x \in \left( { - 2;0} \right) \Leftrightarrow 4m \le  - \dfrac{4}{3} \Leftrightarrow m \le  - \dfrac{1}{3}$

Vậy $m \leqslant  - \dfrac{1}{3}$

Có: $y\left( x \right) = {x^3} + 3m{x^2} - 3x$ $\Rightarrow y'\left( x \right) = 3{x^2} + 6mx - 3$ 

Phương trình đường thẳng $d$ đi qua $2$ cực trị của $(C)$ nên $\left( {{x_o};{y_o}} \right) \in d$  thỏa mãn:

$\begin{array}{l}\left\{ \begin{array}{l}y'\left( {{x_o}} \right) = 0\\{y_o} = x_o^3 + 3mx_0^2 - 3{x_o}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x_o^2 + 6m{x_o} - 3 = 0\\{y_o} = {x_o}\left( {x_o^2 + 2m{x_o}} \right) - 3{x_0} + mx_0^2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x_o^2 + 2m{x_o} = 1\\{y_o} =  - 2{x_o} + mx_o^2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x_o^2 =  - 2m{x_o} + 1\\{y_o} =  - 2{x_o} + m\left( { - 2m{x_o} + 1} \right)\end{array} \right.\\ \Rightarrow {y_o} =  - 2\left( {{m^2} + 1} \right){x_o} + m\end{array}$

Ta có $y' = 3{x^2} + 12x + 3\left( {m + 2} \right) = 3\left[ {{x^2} + 4x + \left( {m + 2} \right)} \right].$

Yêu cầu bài toán $\Leftrightarrow y' = 0$ có hai nghiệm phân biệt ${x_1},{\rm{ }}{x_2}$ thỏa mãn ${x_1} <  - 1 < {x_2}$

- Hàm số có hai điểm cực trị $\Leftrightarrow \Delta ' = 4 - \left( {m + 2} \right) = 2 - m > 0 \Leftrightarrow m < 2$

Hai điểm cực trị thỏa mãn ${x_1} <  - 1 < {x_2}$ $\Leftrightarrow$ phương trình $y' = 0$ có hai nghiệm phân biệt$\Leftrightarrow y'\left( { - 1} \right) < 0 \Leftrightarrow m < 1.$

TXĐ: $D = \mathbb{R}$

$y' = 3{x^2} - 6mx.$

Ta có: $y' = 0 \Leftrightarrow \left[ \begin{gathered}x = 0 \Rightarrow y = 6 \hfill \\x = 2m \Rightarrow y =  -  4{m^3} + 6 \hfill \\ \end{gathered}  \right.$

$y^{\prime}=0 \Leftrightarrow\left[\begin{array}{c}x=0 \Rightarrow y=6 \\ x=2 m \Rightarrow y=-4 m^{3}+6\end{array}\right.$

Xét TH1: $m = 0$. Hàm số đồng biến trên $\left[ {0;3} \right]$ $\Rightarrow \mathop {Min}\limits_{\left[ {0;3} \right]} y = y\left( 0 \right) = 6 \Rightarrow$ loại.

Xét TH2: $m \geqslant \dfrac{3}{2} \Rightarrow 2m \ge 3 > 0$. Khi đó, hàm số nghịch biến trên $\left[ {0;3} \right] \subset \left[ {0;2m} \right]$

$\Rightarrow \mathop {Min}\limits_{\left[ {0;3} \right]} y = y\left( 3 \right) = 33 - 27m = 2 \Rightarrow m = \dfrac{{31}}{{27}} < \dfrac{3}{2}$(loại)

Xét TH3: $\dfrac{3}{2} > m > 0 \Rightarrow 3 > 2m > 0$ thì đồ thị hàm số có điểm cực đại là $\left( {0;6} \right)$ và điểm cực tiểu là $\left( {2m, -  4{m^3} + 6} \right).$

Khi đó , GTNN trên $\left[ {0;3} \right]$ là $y\left( {2m} \right) =  - 4{m^3} + 6$ $\Rightarrow  - 4{m^3} + 6 = 2 \Leftrightarrow {m^3} = 1 \Leftrightarrow m = 1$ (thỏa mãn)

Xét TH4: $m < 0 \Rightarrow \left( {0;6} \right)$ là điểm cực tiểu của đồ thị hàm số và trên $\left[ {0;3} \right]$ hàm số đồng biến.

$\Rightarrow {y_{min}} = 6 \Rightarrow$ loại.

Vậy $m = 1$ là giá trị cần tìm.