Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: b
Có: $y\left( x \right) = {x^3} + 3m{x^2} - 3x$ $ \Rightarrow y'\left( x \right) = 3{x^2} + 6mx - 3$
Phương trình đường thẳng $d$ đi qua $2$ cực trị của $(C)$ nên $\left( {{x_o};{y_o}} \right) \in d$ thỏa mãn:
\(\begin{array}{l}\left\{ \begin{array}{l}y'\left( {{x_o}} \right) = 0\\{y_o} = x_o^3 + 3mx_0^2 - 3{x_o}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x_o^2 + 6m{x_o} - 3 = 0\\{y_o} = {x_o}\left( {x_o^2 + 2m{x_o}} \right) - 3{x_0} + mx_0^2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x_o^2 + 2m{x_o} = 1\\{y_o} = - 2{x_o} + mx_o^2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x_o^2 = - 2m{x_o} + 1\\{y_o} = - 2{x_o} + m\left( { - 2m{x_o} + 1} \right)\end{array} \right.\\ \Rightarrow {y_o} = - 2\left( {{m^2} + 1} \right){x_o} + m\end{array}\)
Hướng dẫn giải:
- Gọi ${x_0}$ là một điểm cực trị của hàm số $y = f\left( x \right)$, khi đó \(\left\{ \begin{array}{l}y'\left( {{x_o}} \right) = 0\\{y_o} = x_o^3 + 3mx_0^2 - 3{x_o}\end{array} \right.\)
- Từ hệ trên ta tìm được phương trình đường thẳng đi qua $\left( {{x_0};{y_0}} \right)$.
Giải thích thêm:
Các em cũng có thể giải bài toán bằng cách khác:
- Tính $y'$.
- Thực hiện phép chia $y$ cho $y'$ ta sẽ tìm được đa thức dư là kết quả bài toán.
Có: $y\left( x \right) = {x^3} + 3m{x^2} - 3x$ $ \Rightarrow y'\left( x \right) = 3{x^2} + 6mx - 3$
Phương trình đường thẳng $d$ đi qua $2$ cực trị của $(C)$ nên $\left( {{x_o};{y_o}} \right) \in d$ thỏa mãn:
\(\begin{array}{l}\left\{ \begin{array}{l}y'\left( {{x_o}} \right) = 0\\{y_o} = x_o^3 + 3mx_0^2 - 3{x_o}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x_o^2 + 6m{x_o} - 3 = 0\\{y_o} = {x_o}\left( {x_o^2 + 2m{x_o}} \right) - 3{x_0} + mx_0^2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x_o^2 + 2m{x_o} = 1\\{y_o} = - 2{x_o} + mx_o^2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x_o^2 = - 2m{x_o} + 1\\{y_o} = - 2{x_o} + m\left( { - 2m{x_o} + 1} \right)\end{array} \right.\\ \Rightarrow {y_o} = - 2\left( {{m^2} + 1} \right){x_o} + m\end{array}\)
Hướng dẫn giải:
- Gọi ${x_0}$ là một điểm cực trị của hàm số $y = f\left( x \right)$, khi đó \(\left\{ \begin{array}{l}y'\left( {{x_o}} \right) = 0\\{y_o} = x_o^3 + 3mx_0^2 - 3{x_o}\end{array} \right.\)
- Từ hệ trên ta tìm được phương trình đường thẳng đi qua $\left( {{x_0};{y_0}} \right)$.
Giải thích thêm:
Các em cũng có thể giải bài toán bằng cách khác:
- Tính $y'$.
- Thực hiện phép chia $y$ cho $y'$ ta sẽ tìm được đa thức dư là kết quả bài toán.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số $f\left( x \right)$ xác định trên $\left[ {0;2} \right]$ và có GTNN trên đoạn đó bằng $5$. Chọn kết luận đúng:
Tìm tất cả các giá trị của $m$ để hàm số $y = - \dfrac{1}{3}{x^3} + \dfrac{{m{x^2}}}{3} + 4$ đạt cực đại tại $x = 2?$
Cho hàm số $y = {x^3} - 3m{x^2} + 6$, giá trị nhỏ nhất của hàm số trên $\left[ {0;3} \right]$ bằng $2$ khi:
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình bên dưới, chọn khẳng định sai:
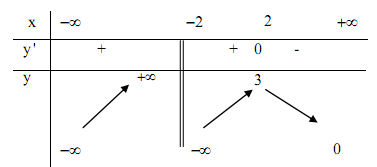
Trong các hàm số dưới đây, hàm số nào không đồng biến trên $R?$
Cho hàm số $y = f\left( x \right)$ có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng?
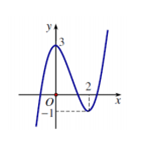
Hình dưới là đồ thị hàm số \(y = f'\left( x \right)\). Hỏi hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
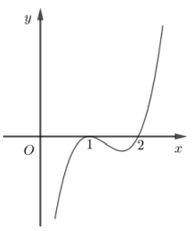
Cho hàm số $y = {x^3} + 6{x^2} + 3\left( {m + 2} \right)x - m - 6$ với \(m\) là tham số thực. Tìm tất cả các giá trị của \(m\) để hàm số có hai điểm cực trị ${x_1},{\rm{ }}{x_2}$ thỏa mãn ${x_1} < - 1 < {x_2}$.
Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\left( {a;b} \right)$. Nếu $f'\left( x \right)$ đổi dấu từ âm sang dương qua điểm ${x_0}$ thuộc \((a;b)\) thì
Tìm $m$ để hàm số $y = \dfrac{{{x^3}}}{3} - 2m{x^2} + 4mx + 2$ nghịch biến trên khoảng $\left( { - 2;0} \right)$.

