Cho hàm số $y = {x^3} + 6{x^2} + 3\left( {m + 2} \right)x - m - 6$ với \(m\) là tham số thực. Tìm tất cả các giá trị của \(m\) để hàm số có hai điểm cực trị ${x_1},{\rm{ }}{x_2}$ thỏa mãn ${x_1} < - 1 < {x_2}$.
A.
$m > 1$
B.
$m < 1$
C.
$m > - 1$
D.
$m < - 1$
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: b
Ta có $y' = 3{x^2} + 12x + 3\left( {m + 2} \right) = 3\left[ {{x^2} + 4x + \left( {m + 2} \right)} \right].$
Yêu cầu bài toán $ \Leftrightarrow y' = 0$ có hai nghiệm phân biệt ${x_1},{\rm{ }}{x_2}$ thỏa mãn ${x_1} < - 1 < {x_2}$
- Hàm số có hai điểm cực trị \( \Leftrightarrow \Delta ' = 4 - \left( {m + 2} \right) = 2 - m > 0 \Leftrightarrow m < 2\)
Hai điểm cực trị thỏa mãn \({x_1} < - 1 < {x_2}\) \( \Leftrightarrow \) phương trình \(y' = 0\) có hai nghiệm phân biệt\( \Leftrightarrow y'\left( { - 1} \right) < 0 \Leftrightarrow m < 1.\)
Hướng dẫn giải:
- Tìm điều kiện để hàm số có hai điểm cực trị.
- Tìm điều kiện để hai điểm cực trị thỏa mãn điều kiện bài cho.
Giải thích thêm:
Nhận xét. Nhắc lại kiến thức lớp dưới \(''\)phương trình \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\,\,\left( {{x_1} < {x_2}} \right)\) thỏa mãn \({x_1} < {x_0} < {x_2} \Leftrightarrow af\left( {{x_0}} \right) < 0''.\)
Ta có $y' = 3{x^2} + 12x + 3\left( {m + 2} \right) = 3\left[ {{x^2} + 4x + \left( {m + 2} \right)} \right].$
Yêu cầu bài toán $ \Leftrightarrow y' = 0$ có hai nghiệm phân biệt ${x_1},{\rm{ }}{x_2}$ thỏa mãn ${x_1} < - 1 < {x_2}$
- Hàm số có hai điểm cực trị \( \Leftrightarrow \Delta ' = 4 - \left( {m + 2} \right) = 2 - m > 0 \Leftrightarrow m < 2\)
Hai điểm cực trị thỏa mãn \({x_1} < - 1 < {x_2}\) \( \Leftrightarrow \) phương trình \(y' = 0\) có hai nghiệm phân biệt\( \Leftrightarrow y'\left( { - 1} \right) < 0 \Leftrightarrow m < 1.\)
Hướng dẫn giải:
- Tìm điều kiện để hàm số có hai điểm cực trị.
- Tìm điều kiện để hai điểm cực trị thỏa mãn điều kiện bài cho.
Giải thích thêm:
Nhận xét. Nhắc lại kiến thức lớp dưới \(''\)phương trình \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\,\,\left( {{x_1} < {x_2}} \right)\) thỏa mãn \({x_1} < {x_0} < {x_2} \Leftrightarrow af\left( {{x_0}} \right) < 0''.\)
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số $f\left( x \right)$ xác định trên $\left[ {0;2} \right]$ và có GTNN trên đoạn đó bằng $5$. Chọn kết luận đúng:
Tìm tất cả các giá trị của $m$ để hàm số $y = - \dfrac{1}{3}{x^3} + \dfrac{{m{x^2}}}{3} + 4$ đạt cực đại tại $x = 2?$
Cho hàm số $y = {x^3} - 3m{x^2} + 6$, giá trị nhỏ nhất của hàm số trên $\left[ {0;3} \right]$ bằng $2$ khi:
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình bên dưới, chọn khẳng định sai:
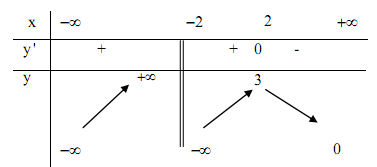
Trong các hàm số dưới đây, hàm số nào không đồng biến trên $R?$
Hãy lập phương trình đường thẳng $(d)$ đi qua các điểm cực đại và cực tiểu của đồ thị hàm số $y = {x^3} + 3m{x^2} - 3x$
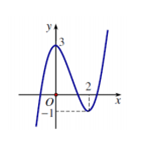
Cho hàm số $y = f\left( x \right)$ có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng?
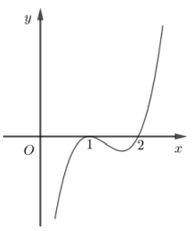
Hình dưới là đồ thị hàm số \(y = f'\left( x \right)\). Hỏi hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\left( {a;b} \right)$. Nếu $f'\left( x \right)$ đổi dấu từ âm sang dương qua điểm ${x_0}$ thuộc \((a;b)\) thì
Tìm $m$ để hàm số $y = \dfrac{{{x^3}}}{3} - 2m{x^2} + 4mx + 2$ nghịch biến trên khoảng $\left( { - 2;0} \right)$.

