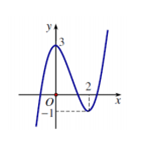
Cho hàm số $y = f\left( x \right)$ có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng?
A.
$\mathop{\max}\limits_{x\in\mathbb{R}}f\left(x\right)=3$
B.
Hàm số đồng biến trên khoảng$\left( { - \infty ;3} \right)$
C.
Giá trị cực tiểu của hàm số bằng 2
D.
$\mathop {\min }\limits_{x \in \left[ {0;4} \right]} f\left( x \right) = - 1$
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: d
A sai vì $y=3$ là giá trị cực đại của hàm số, không phải giá trị lớn nhất.
B sai vì hàm số đồng biến trên các khoảng $\left( { - \infty ;0} \right),\left( {2; + \infty } \right)$.
C sai vì $x=2$ là điểm cực tiểu của hàm số không phải giá trị cực tiểu.
D đúng vì trên đoạn $\left[ {0;4} \right]$ thì hàm số đạt GTNN (cũng là giá trị cực tiểu) bằng $ - 1$ đạt được tại $x = 2$.
Hướng dẫn giải:
Quan sát đồ thị hàm số và rút ra các nhận xét về cực đại, cực tiểu, GTLN, GTNN, khoảng đồng biến, nghịch biến.
Giải thích thêm:
Học sinh thường nhầm lẫn cách tìm GTLN, GTNN của hàm số với giá trị cực đại, giá trị cực tiểu của hàm số. nên có thể chọn A là sai.
A sai vì $y=3$ là giá trị cực đại của hàm số, không phải giá trị lớn nhất.
B sai vì hàm số đồng biến trên các khoảng $\left( { - \infty ;0} \right),\left( {2; + \infty } \right)$.
C sai vì $x=2$ là điểm cực tiểu của hàm số không phải giá trị cực tiểu.
D đúng vì trên đoạn $\left[ {0;4} \right]$ thì hàm số đạt GTNN (cũng là giá trị cực tiểu) bằng $ - 1$ đạt được tại $x = 2$.
Hướng dẫn giải:
Quan sát đồ thị hàm số và rút ra các nhận xét về cực đại, cực tiểu, GTLN, GTNN, khoảng đồng biến, nghịch biến.
Giải thích thêm:
Học sinh thường nhầm lẫn cách tìm GTLN, GTNN của hàm số với giá trị cực đại, giá trị cực tiểu của hàm số. nên có thể chọn A là sai.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số $f\left( x \right)$ xác định trên $\left[ {0;2} \right]$ và có GTNN trên đoạn đó bằng $5$. Chọn kết luận đúng:
Tìm tất cả các giá trị của $m$ để hàm số $y = - \dfrac{1}{3}{x^3} + \dfrac{{m{x^2}}}{3} + 4$ đạt cực đại tại $x = 2?$
Cho hàm số $y = {x^3} - 3m{x^2} + 6$, giá trị nhỏ nhất của hàm số trên $\left[ {0;3} \right]$ bằng $2$ khi:
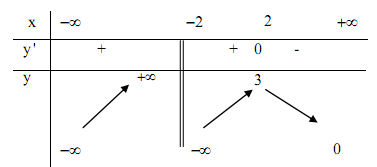
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình bên dưới, chọn khẳng định sai:
Trong các hàm số dưới đây, hàm số nào không đồng biến trên $R?$
Hãy lập phương trình đường thẳng $(d)$ đi qua các điểm cực đại và cực tiểu của đồ thị hàm số $y = {x^3} + 3m{x^2} - 3x$
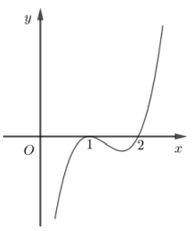
Hình dưới là đồ thị hàm số \(y = f'\left( x \right)\). Hỏi hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
Cho hàm số $y = {x^3} + 6{x^2} + 3\left( {m + 2} \right)x - m - 6$ với \(m\) là tham số thực. Tìm tất cả các giá trị của \(m\) để hàm số có hai điểm cực trị ${x_1},{\rm{ }}{x_2}$ thỏa mãn ${x_1} < - 1 < {x_2}$.
Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\left( {a;b} \right)$. Nếu $f'\left( x \right)$ đổi dấu từ âm sang dương qua điểm ${x_0}$ thuộc \((a;b)\) thì
Tìm $m$ để hàm số $y = \dfrac{{{x^3}}}{3} - 2m{x^2} + 4mx + 2$ nghịch biến trên khoảng $\left( { - 2;0} \right)$.

