Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
Hỏi bàiĐề kiểm tra 15 phút chương 1: Hàm số - Đề số 2
-
Hocon247
-
12 câu hỏi
-
45 phút
-
614 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Đề thi THPT QG - 2021 - mã 101
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
Đồ thị là dạng của hàm số bậc 4 trùng phương, nhánh cuối của đồ thị đi xuống \( \Rightarrow \) hệ số của \({x^4}\) mang dấu âm.
Hướng dẫn giải:
Dựa vào đồ thị nhận dạng hàm số.
Cho hàm số $y = a{x^4} + b{x^2} + c\left( {a > 0} \right)$ có ba cực trị. Nếu ${y_{CD}} < 0$ thì:
Dễ thấy hàm số bậc bốn trùng phương có cực đại, cực tiểu thì ${y_{CT}} < {y_{CD}}$ nên ${y_{CD}} < 0 \Rightarrow {y_{CT}} < 0$.
Hàm số nào có thể có đồ thị dạng như hình vẽ?
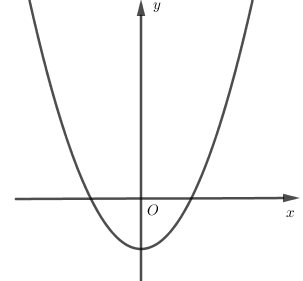
Dạng đồ thị đã cho có thể là của hàm số bậc hai hoặc hàm bậc bốn trùng phương.
Hướng dẫn giải:
Quan sát dạng đồ thị và đối chiếu với các đáp án bài cho.
Nếu điểm cực đại của đồ thị hàm số bậc ba nằm ở trục hoành thì:
Hàm số bậc ba luôn có ${y_{CD}} > {y_{CT}}$ nên nếu ${y_{CD}} = 0$ thì ${y_{CT}} < 0$.
Do đó điểm cực tiểu của đồ thị hàm số luôn nằm dưới trục hoành.
Cho bảng biến thiên hình bên, hàm số đồng biến trên:
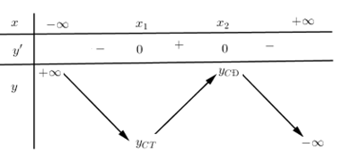
Quan sát bảng biến thiên ta thấy \(y' > 0,\forall x \in \left( {{x_1};{x_2}} \right)\) nên hàm số nghịch biến trên khoảng \(\left( {{x_1};{x_2}} \right)\)
Hướng dẫn giải:
Khoảng làm cho đạo hàm mang dấu dương là khoảng hàm số đồng biến.
Hàm số $y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)$ có $1$ cực trị nếu và chỉ nếu:
Ta có: $y' = 4a{x^3} + 2bx = 2x\left( {2a{x^2} + b} \right)$.
Hàm số có $1$ cực trị $ \Leftrightarrow y' = 0$ có $1$ nghiệm duy nhất hay $y'=0$ vô nghiệm hoặc có nghiệm kép
\( \Leftrightarrow \left[ \begin{array}{l}ab > 0\\b \ge 0\end{array} \right. \Leftrightarrow ab \ge 0\)
Giải thích thêm:
HS thường nhầm lẫn khi xét phương trình $2a{x^2} + b = 0$ vô nghiệm thì chọn ngay $b > 0$ mà không để ý điều kiện của $a$ và chọn đáp án C là sai.
Hàm số bậc bốn trùng phương xác định trên:
Hàm số bậc bốn trùng phương xác định trên \(R\).
Hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ, chọn kết luận đúng:
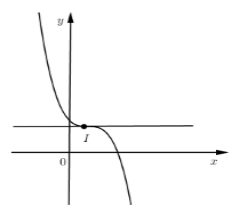
Quan sát đồ thị ta thấy \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty ;\mathop {\lim }\limits_{x \to - \infty } y = + \infty \) nên \(a < 0\).
Chọn kết luận đúng:
Đáp án A: Hàm số bậc ba có $2$ cực trị thì đồ thị hàm số cắt trục hoành tại $3$ điểm phân biệt nếu ${y_{CD}}.{y_{CT}} < 0$ hoặc chỉ cắt $Ox$ tại 1 điểm nếu ${y_{CD}}.{y_{CT}} > 0$ nên A sai.
Đáp án B: Đồ thị hàm số bậc ba luôn cắt trục hoành tại ít nhất $1$ điểm nhưng chưa chắc đó là điểm uốn nên B sai.
Đáp án C: Đồ thị hàm số bậc ba cắt trục hoành tại $3$ điểm phân biệt thì hàm số có hai điểm cực trị là đúng.
Đáp án D: Đồ thị hàm số bậc ba cắt trục hoành tại $1$ điểm duy nhất thì nó không có cực trị hoặc có cực trị nhưng hai giá trị cực trị cùng dấu nên D sai.
Giải thích thêm:
HS cần nắm rõ các dạng đồ thị hàm số bậc ba để nhận xét, tránh chọn nhầm các đáp án A hoặc D là sai.
Cho hàm số \(y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)\) có 1 cực trị. Khi đó, đồ thị hàm số nằm hoàn toàn phía dưới trục hoành thì:
Hàm số chỉ có 1 cực trị thì \(y' = 0\) có 1 nghiệm \( \Leftrightarrow ab \ge 0\), khi đó đồ thị có dạng:
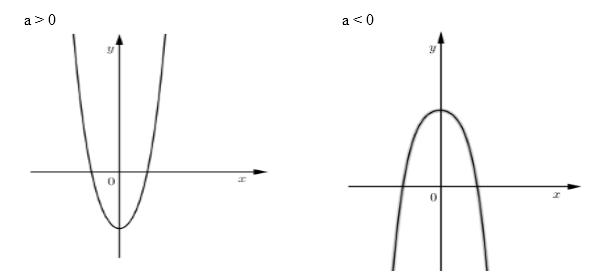
Trong hai trường hợp trên ta thấy nếu đồ thị hàm số nằm hoàn toàn phía dưới trục hoành thì chỉ xảy ra trường hợp \(a < 0\), do đó \(b \le 0\) và điểm cực tiểu \(\left( {0;c} \right)\) cũng phải nằm phía dưới trục hoành hay \(c < 0\).
Hướng dẫn giải:
Vẽ các dạng đồ thị hàm số bậc bốn trùng phương có 1 cực trị và kết hợp với điều kiện bài cho để tìm ra đáp án đúng.
Đồ thị trong hình dưới là đồ thị của một trong bốn hàm số cho trong các phương án sau đây, đó là hàm số nào?
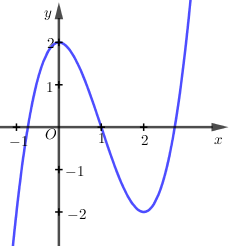
Ta sử dụng theo cách trắc nghiệm để giải bài toán
Hàm số có nét cuối đi lên nên ta có: $a > 0$. Nên ta loại đáp án A.
Đồ thị hàm số đi qua điểm $A(1;0) $ ta thay tọa độ điểm A vào 3 đáp án B, C, D thì đáp án D loại.
Đồ thị hàm số đi qua điểm $B(0;2)$ nên ta thay tọa độ điểm B vào đáp án B và C thì ta loại được đáp án C.
Hướng dẫn giải:
Dựa vào dạng của đồ thị hàm số, các điểm đi qua và các điểm cực trị của đồ thị hàm số để kết luận hàm số đó.
Cho hàm số $y = f\left( x \right) = a{x^4} + {b^2}{x^2} + 1\left( {a \ne 0} \right)$ . Trong các khẳng định dưới đây, khẳng định nào là đúng?
Ta có: $y' = 4a{x^3} + 2{b^2}{x}$
Dễ thấy $x = 0$ luôn là nghiệm của $y'$.
Mà hàm bậc 4 luôn có cực trị
$ \Rightarrow $ đáp án D đúng
Hướng dẫn giải:
Khảo sát hàm bậc 4 trùng phương, đối chiếu các đáp án và chọn kết luận đúng.
Giải thích thêm:
Có thể loại ngay các đáp án A, B vì dùng sai ngôn ngữ: Các khái niệm “tâm đối xứng, trục đối xứng” chỉ dành cho “đồ thị hàm số” chứ không phải của “hàm số”.
