Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: a
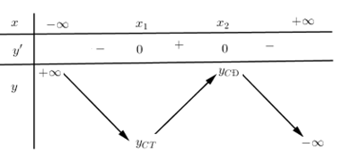
Quan sát bảng biến thiên ta thấy \(y' > 0,\forall x \in \left( {{x_1};{x_2}} \right)\) nên hàm số nghịch biến trên khoảng \(\left( {{x_1};{x_2}} \right)\)
Hướng dẫn giải:
Khoảng làm cho đạo hàm mang dấu dương là khoảng hàm số đồng biến.
Quan sát bảng biến thiên ta thấy \(y' > 0,\forall x \in \left( {{x_1};{x_2}} \right)\) nên hàm số nghịch biến trên khoảng \(\left( {{x_1};{x_2}} \right)\)
Hướng dẫn giải:
Khoảng làm cho đạo hàm mang dấu dương là khoảng hàm số đồng biến.
CÂU HỎI CÙNG CHỦ ĐỀ
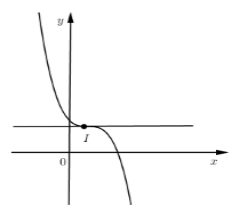
Hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ, chọn kết luận đúng:
Hàm số $y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)$ có $1$ cực trị nếu và chỉ nếu:
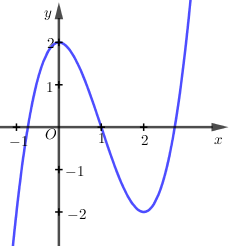
Đồ thị trong hình dưới là đồ thị của một trong bốn hàm số cho trong các phương án sau đây, đó là hàm số nào?
Nếu điểm cực đại của đồ thị hàm số bậc ba nằm ở trục hoành thì:
Cho hàm số $y = a{x^4} + b{x^2} + c\left( {a > 0} \right)$ có ba cực trị. Nếu ${y_{CD}} < 0$ thì:
Đề thi THPT QG - 2021 - mã 101
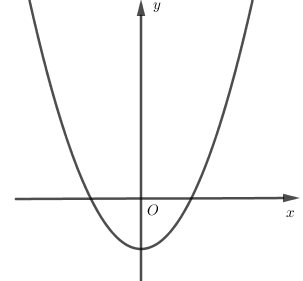
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
Cho hàm số \(y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)\) có 1 cực trị. Khi đó, đồ thị hàm số nằm hoàn toàn phía dưới trục hoành thì:
Cho hàm số $y = f\left( x \right) = a{x^4} + {b^2}{x^2} + 1\left( {a \ne 0} \right)$ . Trong các khẳng định dưới đây, khẳng định nào là đúng?