Đề kiểm tra 1 tiết chương 1: Hàm số - Đề số 3
-
Hocon247
-
25 câu hỏi
-
45 phút
-
646 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Hệ số góc của tiếp tuyến của đồ thị hàm số $y = \dfrac{{{x^4}}}{4} + \dfrac{{{x^2}}}{2} - 1$ tại điểm có hoành độ $x = - 1$ là:
Ta có $y' = {x^3} + x$
$ \Rightarrow $ Hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ $x=-1$ là $k = y'( - 1) = - 2$
Hướng dẫn giải:
Hệ số góc của tiếp tuyến của đồ thị hàm số $y = f\left( x \right)$ tại điểm có hoành độ $x = {x_0}$ là $k = f'\left( {{x_0}} \right)$.
Cho hàm số $f\left( x \right)$ xác định và có đạo hàm trên $\left( {a;b} \right)$. Nếu $f'\left( x \right) < 0,\forall x \in \left( {a;b} \right)$ thì:
Sử dụng định lý về xét tính đồng biến, nghịch biến của hàm số trên một khoảng đã nêu ở phần phương pháp, ở đây khoảng $K=(a;b)$ ta được:
Hàm số $y = f\left( x \right)$ xác định và có đạo hàm $f'\left( x \right) < 0,\forall x \in \left( {a;b} \right)$ thì $f\left( x \right)$ nghịch biến trên $\left( {a;b} \right)$.
Hướng dẫn giải:
Sử dụng định lý:
Định lý: Cho hàm số $y = f\left( x \right)$ xác định và có đạo hàm trên $K$.
a) Nếu $f'\left( x \right) > 0,\forall x \in K$ thì hàm số $y = f\left( x \right)$ đồng biến trên $K$.
b) Nếu $f'\left( x \right) < 0,\forall x \in K$ thì hàm số $y = f\left( x \right)$ nghịch biến trên $K$.
Số cực trị của hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) là:
Hàm phân thức bậc nhất trên bậc nhất không có cực trị.
Giá trị lớn nhất của hàm số $f\left( x \right) = \dfrac{{\sin x}}{x}$ trên đoạn $\left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]$ là:
TXĐ: $x \ne 0$.
$f'\left( x \right) = \dfrac{{x\cos x - \sin x}}{{{x^2}}} < 0 \forall x \in \left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]$
Thật vậy,
Xét hàm \(g\left( x \right) = x\cos x - \sin x\) trên \(\left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]\) có:
\(g'\left( x \right) = \cos x - x\sin x - \cos x\) \( = - x\sin x < 0,\forall x \in \left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]\)
Do đó hàm số \(g\left( x \right)\) nghịch biến trên \(\left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]\).
Suy ra \(g\left( x \right) \le g\left( {\dfrac{\pi }{6}} \right)\) \( = \dfrac{\pi }{6}.\cos \dfrac{\pi }{6} - \sin \dfrac{\pi }{6} < 0\) hay \(x\cos x - \sin x < 0\) với \(\forall x \in \left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]\)
$ \Rightarrow \mathop {\max }\limits_{\left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]} f\left( x \right) = f\left( {\dfrac{\pi }{6}} \right) = \dfrac{3}{\pi }$.
Hướng dẫn giải:
Sử dụng phương pháp tìm GTLN, GTNN của hàm số:
- Tính \(y'\) và tìm các nghiệm của \(y' = 0\).
- Tính giá trị hàm số tại các điểm đặc biệt và kết luận.
Tìm tất cả các giá trị của $m$ để hàm số $y = \dfrac{{m{x^3}}}{3} - m{x^2} + x - 1$ có cực đại và cực tiểu.
TXĐ: $D = R$
TH1: $m = 0 \to y = x - 1.$
Hàm số không có cực trị.
TH2: $m \ne 0$.
Ta có: $y = \dfrac{{m{x^3}}}{3} - m{x^2} + x - 1$ $ \Rightarrow y' = m{x^2} - 2mx + 1.$
Để hàm số cho có cực đại, cực tiểu thì phương trình $y' = 0$ phải có $2$ nghiệm phân biệt
$ \Rightarrow \Delta ' = {m^2} - m > 0 \Leftrightarrow \left[ \begin{gathered} m < 0 \hfill \\ m > 1 \hfill \\\end{gathered} \right..$
Hướng dẫn giải:
- Bước 1: Tính $y'$.
- Bước 2: Hàm số có cực đại và cực tiểu $ \Leftrightarrow y' = 0$ có hai nghiệm phân biệt $ \Leftrightarrow \Delta > 0$.
- Bước 3: Kết luận.
Giải thích thêm:
Học sinh cần nhớ xét trường hợp $m=0$ khi hệ số trước $x$ có mũ cao nhất chứa tham số.
Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:
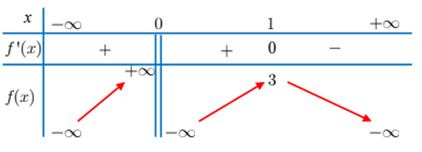
Với các giá trị thực của tham số \(m\), phương trình \(f\left( x \right)=m\) có nhiều nhất bao nhiêu nghiệm?
Quan sát đồ thị hàm số ta thấy:
+) Với \(m < 3\) thì đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại \(3\) điểm phân biệt.
+) Với \(m = 3\) thì đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại \(2\) điểm phân biệt.
+) Với \(m > 3\) thì đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại duy nhất \(1\) điểm.
Vậy đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại nhiều nhất \(3\) điểm.
Do đó phương trình đã cho có nhiều nhất \(3\) nghiệm.
Hướng dẫn giải:
Số nghiệm của phương trình bằng số giao điểm của đường thẳng \(y = m\) với đồ thị hàm số \(y = f\left( x \right)\).
Giả sử $y = f\left( x \right)$ có đạo hàm cấp hai trên $\left( {a;b} \right)$. Nếu $\left\{ \begin{gathered}f'\left( {{x_0}} \right) = 0 \hfill \\ f''\left( {{x_0}} \right) > 0 \hfill \\ \end{gathered} \right.$ thì
Nếu $\left\{ \begin{gathered} f'\left( {{x_0}} \right) = 0 \hfill \\ f''\left( {{x_0}} \right) > 0 \hfill \\\end{gathered} \right.$ thì ${x_0}$ là một điểm cực tiểu của hàm số.
Hướng dẫn giải:
a) Nếu $\left\{ \begin{gathered} f'\left( {{x_0}} \right) = 0 \hfill \\f''\left( {{x_0}} \right) > 0 \hfill \\ \end{gathered} \right.$ thì ${x_0}$ là một điểm cực tiểu của hàm số.
b) Nếu $\left\{ \begin{gathered}f'\left( {{x_0}} \right) = 0 \hfill \\f''\left( {{x_0}} \right) < 0 \hfill \\\end{gathered} \right.$ thì ${x_0}$ là một điểm cực đại của hàm số.
Cho hàm số $y = a{x^4} + b{x^2} + c$ có bảng biến thiên như hình vẽ. Chọn kết luận đúng:
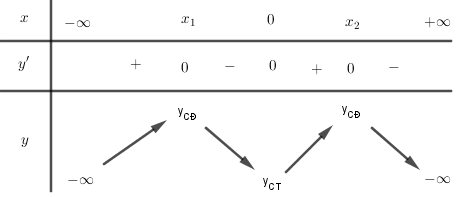
Từ bảng biến thiên ta thấy $\mathop {\lim }\limits_{x \to \pm \infty } y = - \infty $ nên $a < 0$.
Tập xác định của hàm số $y = - \dfrac{1}{2}{x^3} + 2x - 1$ là:
Hàm đa thức bậc ba xác định trên $R$.
Cho hàm số \(y = a{x^4} + b{x^2} + c\left( {a < 0} \right)\) có \(3\) cực trị. Nếu \({y_{CT}} > 0\) thì:
Dễ thấy hàm số bậc bốn trùng phương có cực đại, cực tiểu thì \({y_{CT}} < {y_{CD}}\) nên nếu \({y_{CT}} > 0\) thì \({y_{CD}} > 0\).
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là sai?
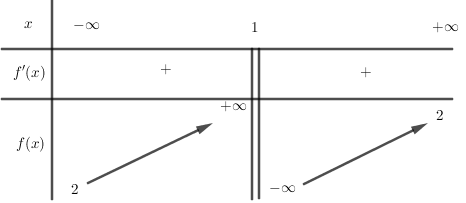
A đúng vì đồ thị hàm số có đường tiệm cận đứng là \(x = 1\)
B đúng vì hàm số luôn đồng biến nên không có cực trị
C đúng vì đồ thị hàm số có đường tiệm cận ngang \(y = 2\)
D sai vì hàm số đồng biến trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\) chứ không đồng biến trên toàn bộ tập số thực \(\mathbb{R}\)
Hướng dẫn giải:
Quan sát bảng biến thiên và tìm các đường tiệm cận của đồ thị hàm số, các khoảng đồng biến, nghịch biến của hàm số.
Hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ, chọn kết luận đúng:
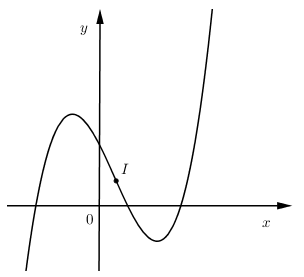
Quan sát đồ thị ta thấy $\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = - \infty $ nên $a > 0$.
Nếu $\mathop {\lim }\limits_{x \to x_0^ + } y = + \infty $ thì đường thẳng $x = {x_0}$ là:
Nếu $\mathop {\lim }\limits_{x \to x_0^ + } y = + \infty $ thì đường thẳng $x = {x_0}$ là tiệm cận đứng của đồ thị hàm số.
Trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số nào có bảng biến thiên như sau?
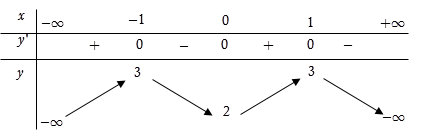
Dựa vào BBT và các phương án lựa chọn, ta thấy:
Đây là dạng hàm số trùng phương có hệ số $a < 0$. Loại A và C.
Mặt khác, đồ thị hàm số đi qua điểm \(\left( {0;2} \right)\) nên loại B.
Hướng dẫn giải:
Quan sát bảng biến thiên, nhận xét hệ số \(a,b,c\) và kết luận.
Đề thi THPT QG - 2021 - mã 102
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{x + 1}}{{x - 2}}\) là đường thẳng có phương trình
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{x + 1}}{{x - 2}}\) là đường thẳng có phương trình \(x = 2\)
Hướng dẫn giải:
Tiệm cận đứng của đồ thị hàm phân thức bậc nhất \(y = \dfrac{{ax + b}}{{cx + d}}\) là \(x = - \dfrac{d}{c}\)
Cho hàm số \(f\left( x \right) = \dfrac{{ax - 1}}{{bx + c}}\,\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:
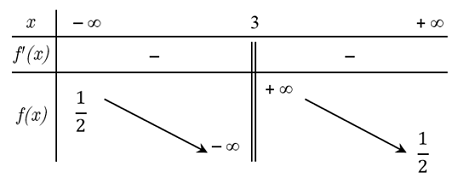
Khẳng định nào dưới đây đúng?
TXĐ: \(D = \mathbb{R}\backslash \left\{ 3 \right\}\).
Dựa vào BBT, ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to \pm \infty } f\left( x \right) = \dfrac{1}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) = + \infty ,\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) = - \infty \end{array} \right. \Rightarrow \left\{ \begin{array}{l}\dfrac{a}{b} = \dfrac{1}{2}\\ - \dfrac{c}{b} = 3\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}a = \dfrac{b}{2}\\c = - 3b\end{array} \right.\)
Ta có: \(f\left( x \right) = \dfrac{{ax - 1}}{{bx + c}}\, \Rightarrow f'\left( x \right) = \dfrac{{ac + b}}{{{{\left( {bx + c} \right)}^2}}}\).
Dựa vào BBT ta thấy \(f'\left( x \right) < 0\,\,\,\forall x \ne 3 \Leftrightarrow ac + b < 0\,\,\forall x \ne 3\)\( \Leftrightarrow \dfrac{b}{2}.\left( { - 3b} \right) + b < 0 \Leftrightarrow \left[ \begin{array}{l}b < 0\\b > \dfrac{2}{3}\end{array} \right.\).
Hướng dẫn giải:
- Đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\,\,\left( {ad \ne bc} \right)\) có đường tiệm cận ngang \(y = \dfrac{a}{c}\), tiệm cận đứng \(x = - \dfrac{d}{c}\). Từ đó biểu diễn a và c theo b.
- Dựa vào chiều biến thiên của đồ thị hàm số, suy ra 1 bất phương trình ẩn b và giải bất phương trình.
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {x^2}\left( {x - 2} \right)\left( {{x^2} - 6x + m} \right)\) với mọi \(x \in \mathbb{R}\). Có bao nhiêu số nguyên \(m\) thuộc đoạn \(\left[ { - 2019;\,2019} \right]\) để hàm số \(g\left( x \right) = f\left( {1 - x} \right)\) nghịch biến trên khoảng \(\left( { - \infty ;\, - 1} \right)\)?
Ta có:
\(g'\left( x \right) = \left[ {f\left( {1 - x} \right)} \right]' = \left( {1 - x} \right)'f'\left( {1 - x} \right)= - f'\left( {1 - x} \right)\)
\(= - {\left( {1 - x} \right)^2}\left( {1 - x - 2} \right)\left[ {{{\left( {1 - x} \right)}^2} - 6\left( {1 - x} \right) + m} \right]\) \( = - {\left( {1 - x} \right)^2}\left( { - 1 - x} \right)\left( {{x^2} + 4x + m - 5} \right) = {\left( {x - 1} \right)^2}\left( {x + 1} \right)\left( {{x^2} + 4x + m - 5} \right)\)
Hàm số \(g\left( x \right)\) nghịch biến trên \(\left( { - \infty ; - 1} \right)\)
\( \Leftrightarrow g'\left( x \right) \le 0,\forall x \in \left( { - \infty ; - 1} \right) \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} + 4x + m - 5} \right) \le 0,\forall x \in \left( { - \infty ; - 1} \right)\)
\( \Leftrightarrow {x^2} + 4x + m - 5 \ge 0,\forall x \in \left( { - \infty ; - 1} \right)\) (do \(x + 1 < 0,\forall x \in \left( { - \infty ; - 1} \right)\))
\( \Leftrightarrow h\left( x \right) = {x^2} + 4x - 5 \ge - m\,\,\forall x \in \left( { - \infty ; - 1} \right)\)
\(\Leftrightarrow - m \le \mathop {\min }\limits_{\left( { - \infty ; - 1} \right]} h\left( x \right)\).
Ta có \(h'\left( x \right) = 2x + 4 = 0 \Leftrightarrow x = - 2\).
BBT:
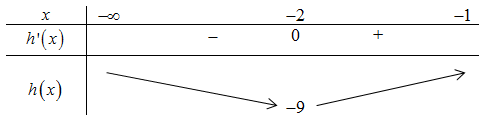
Dựa vào BBT ta có \( - m \le - 9 \Leftrightarrow m \ge 9\).
Mà \(m \in \left[ { - 2019;2019} \right]\) và \(m\) nguyên nên \(m \in \left[ {9;10;11;...;2019} \right]\) hay có \(2019 - 9 + 1 = 2011\) giá trị của \(m\) thỏa mãn.
Hướng dẫn giải:
Hàm số nghịch biến trên \(\left( { - \infty ; - 1} \right)\) nếu \(g'\left( x \right) \le 0,\forall x \in \left( { - \infty ; - 1} \right)\).
Số điểm cực trị của hàm số $y = {(x - 1)^{2017}}$ là
Tập xác định: $D = \mathbb{R}$
$y = {(x - 1)^{2017}} \Rightarrow y' = 2017{(x - 1)^{2016}} \ge 0,\forall x$
Do đó hàm số đồng biến trên $\mathbb{R}$ nên không có cực trị.
Hướng dẫn giải:
- Tính và tìm các nghiệm của $y' = 0$ và các điểm tại đó hàm số không xác định.
- Xét dấu y’ qua các điểm tìm được ở trên và kết luận:
Điểm làm cho đạo hàm đổi dấu là các điểm cực trị của hàm số.
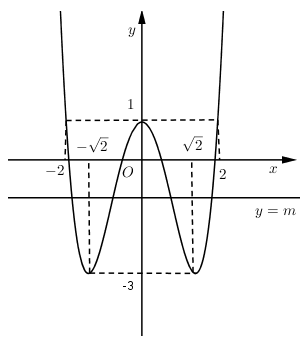
Đồ thị hàm số bên là đồ thị của hàm số $y = {x^4} - 4{x^2} + 1\left( C \right).$ Tìm $m$ để phương trình ${x^4} - 4{x^2} + 1 - m = 0$ có $4$ nghiệm phân biệt
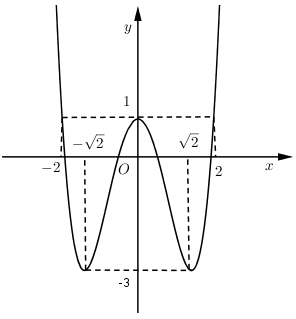
${x^4} - 4{x^2} + 1 - m = 0 \Leftrightarrow {x^4} - 4{x^2} + 1 = m$
Số nghiệm của phương trình ${x^4} - 4{x^2} + 1 - m = 0$ là số giao điểm của đồ thị hàm số $y = {x^4} - 4{x^2} + 1$ và đường thẳng $y = m$.
Þ Để phương trình ${x^4} - 4{x^2} + 1 - m = 0$ có $4$ nghiệm phân biệt $ \Leftrightarrow - 3 < m < 1$
Hướng dẫn giải:
Quan sát đồ thị hàm số và nhận xét: Số nghiệm của phương trình là số giao điểm của đường thẳng với đồ thị hàm số
Đồ thị hàm số \(y = \dfrac{{ax + 2}}{{cx + b}}\) như hình vẽ bên.
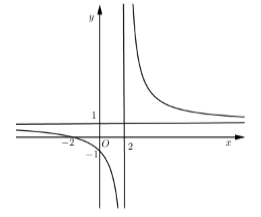
Chọn khẳng định đúng
Ta có đồ thị hàm số\(y = \dfrac{{ax + 2}}{{cx + b}}\) đi qua điểm có tọa độ \(\left( {0; - 1} \right)\).
Thay \(x = 0;\,y = - 1\) vào hàm số ta được \( - 1 = \dfrac{{a.0 + 2}}{{c.0 + b}} \Rightarrow b = - 2\)
Đồ thị hàm số \(y = \dfrac{{ax + 2}}{{cx - 2}}\) có \( \Rightarrow a = 1;\,b = - 2;\,c = 1\)
Hướng dẫn giải:
- Quan sát đồ thị, tìm các điểm đi qua của đồ thị hàm số.
- Tìm các tiệm cận đứng, ngang của đồ thị hàm số.
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( x \right) = {\log _2}m\) có hai nghiệm phân biệt.
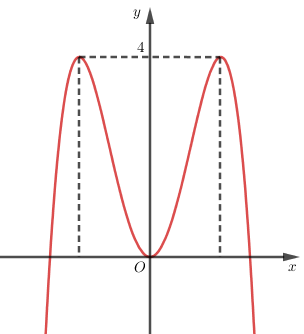
Phương trình \(f\left( x \right) = {\log _2}m\) có hai nghiệm phân biệt \( \Leftrightarrow \) đường thẳng \(y = {\log _2}m\) cắt đồ thị hàm số đã cho tại hai điểm phân biệt \( \Leftrightarrow \left[ \begin{array}{l}{\log _2}m = 4\\{\log _2}m < 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = {2^4}\\0 < m < {2^0}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 16\\0 < m < 1\end{array} \right.\).
Hướng dẫn giải:
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = {\log _2}m\).
Giải thích thêm:
Các em thường quên điều kiện \(m > 0\) dẫn đến chọn nhầm đáp án C là sai
Tiếp tuyến của đồ thị hàm số \(y = \dfrac{{4x - 3}}{{2x + 1}}\) cùng với hai tiệm cận tạo thành một tam giác có diện tích bằng
Chọn \(M\left( { - 1;7} \right)\) thuộc đồ thị hàm số
Có \(y' = \dfrac{{10}}{{{{\left( {2x + 1} \right)}^2}}};y'\left( { - 1} \right) = 10\)
Phương trình tiếp tuyến tại \(M\) : \(y = 10\left( {x + 1} \right) + 7 \Leftrightarrow y = 10x + 17\)
Phương trình các tiệm cận: \(x = - \dfrac{1}{2};y = 2\)
Tam giác \(IAB\) vuông tại \(I\) tạo bởi \(3\) đường trên có \(3\) đỉnh: \(I = \left( { - \dfrac{1}{2};2} \right);A\left( { - \dfrac{1}{2};12} \right);B\left( { - \dfrac{3}{2};2} \right)\) và có diện tích: \(S = \dfrac{1}{2}IA.IB = \dfrac{1}{2}.10.1 = 5\)
Hướng dẫn giải:
+ Chọn 1 điểm thuộc đồ thị hàm số \(y = f\left( x \right)\)
+ Viết phương trình tiếp tuyến
+ Tính diện tích tam giác cần tìm
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình bên:
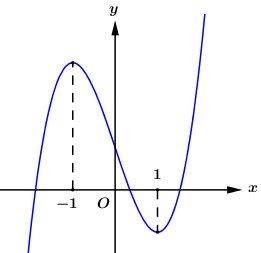
Giá trị nguyên lớn nhất của tham số m để hàm số \(y = f\left( {\left| x \right| - m} \right)\) đồng biến trên khoảng \(\left( {10; + \infty } \right)\) là:
Ta có \(y = f\left( {\left| x \right| - m} \right) = f\left( {\sqrt {{x^2}} - m} \right)\).
\( \Rightarrow y' = \dfrac{{2x}}{{2\sqrt {{x^2}} }}f'\left( {\sqrt {x^2} - m } \right) = \dfrac{x}{{\sqrt {{x^2}} }}f'\left( {\sqrt {x^2} - m } \right)\).
Để hàm số đồng biến trên \(\left( {10; + \infty } \right)\) thì \(y' \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\).
\( \Rightarrow \dfrac{x}{{\sqrt {x^2} }}f'\left( {\sqrt {x^2} - m } \right) \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\) \( \Rightarrow f'\left( {\sqrt {x^2} - m} \right) \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\,\,\left( * \right)\).
Dựa vào đồ thị hàm số ta thấy hàm số đồng biến trên \(\left( {1; + \infty } \right)\) và \(\left( { - \infty ; - 1} \right)\).
Do đó \(\left( * \right) \Leftrightarrow \left[ \begin{array}{l}\sqrt {{x^2}} - m \ge 1\,\,\forall x \in \left( {10; + \infty } \right)\,\,\,\,\,\,\left( 1 \right)\\\sqrt {{x^2}} - m \le - 1\,\,\forall x \in \left( {10; + \infty } \right)\,\,\,\left( 2 \right)\end{array} \right.\)
Xét (1) ta có \(m \le \sqrt {{x^2}} - 1\,\,\forall x \in \left( {10; + \infty } \right) \Rightarrow m \le \mathop {\min }\limits_{\left[ {10; + \infty } \right)} \left( {\sqrt {{x^2}} - 1} \right)\).
Xét \(g\left( x \right) = \sqrt {{x^2}} - 1\) trên khoảng \(\left( {10; + \infty } \right)\) ta có \(g'\left( x \right) = \dfrac{x}{{\sqrt {{x^2}} }} > 0\,\,\forall x \in \left( {10; + \infty } \right)\), do đó hàm số đồng biến trên \(\left( {10; + \infty } \right)\) \( \Rightarrow \mathop {\min }\limits_{\left[ {10; + \infty } \right)} \left( {\sqrt {{x^2}} - 1} \right) = g\left( {10} \right) = 9 \Leftrightarrow m \le 9\).
Xét (2) ta có: \(m \ge \sqrt {{x^2}} + 1\,\,\forall x \in \left( {10; + \infty } \right)\) \( \Rightarrow m \ge \mathop {\max }\limits_{\left[ {10; + \infty } \right)} \left( {\sqrt {{x^2}} + 1} \right)\).
Do \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2}} + 1} \right) = + \infty \) nên hàm số đã cho không có GTLN trên \(\left[ {10; + \infty } \right)\), do đó không tồn tại m thỏa mãn (2).
Vậy \(m \le 9\) nên giá trị nguyên lớn nhất của m bằng 9.
Hướng dẫn giải:
- Biến đổi \(f\left( {\left| x \right| - m} \right) = f\left( {\sqrt {{x^2}} - m} \right)\).
- Tính đạo hàm của hàm số.
- Để hàm số đồng biến trên \(\left( {10; + \infty } \right)\) thì \(y' \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\).
- Dựa vào BBT xác định các khoảng đồng biến của hàm số.
- Sử dụng phương pháp cô lập m.
Giải thích thêm:
Cách 2:
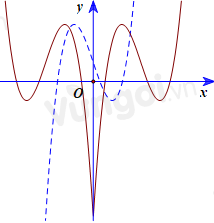
Ta vẽ đồ thị của hàm số \(y = f\left( {\left| x \right| - m} \right)\) với m>0
Tịnh tiến đồ thị hàm số \(y = f\left( x \right)\) sang phải m đơn vị, sau đó bỏ phần đồ thị của \(f\left( {x - m} \right)\) phía bên trái Oy. Lấy đối xứng phần đồ thị hàm số \(f\left( {x - m} \right)\) phía bên phải Oy qua Oy
Khi đó hàm số $f(x)$ đồng biến trên $\left( {1 ; + \infty } \right)$
=> Hàm số $y=f(x-m)$ đồng biến trên $\left( {1 +m; + \infty } \right)$
=> Hàm số $y=f(|x|-m)$ đồng biến trên $\left( {1 +m; + \infty } \right)$
Để hàm số \(y = f\left( {\left| x \right| - m} \right)\) đồng biến trên khoảng \(\left( {10; + \infty } \right)\) thì ta chỉ cần xét khoảng đồng biến của hàm số \(y = f\left( {\left| x \right| - m} \right)\) trên $\left( {1 +m; + \infty } \right)$ là được.
\(\left( {10; + \infty } \right) \subset \left( {1 + m; + \infty } \right) \Rightarrow 1 + m \le 10\)\( \Leftrightarrow m \le 9\).
Vậy giá trị nguyên lớn nhất của m là 9
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số \(y = \left| {3{x^4} - 4{x^3} - 12{x^2} + m} \right|\) có 5 điểm cực trị?
Xét hàm số \(f\left( x \right) = 3{x^4} - 4{x^3} - 12{x^2}\) ta có
\(\begin{array}{l}f'\left( x \right) = 12{x^3} - 12{x^2} - 24x\\f'\left( x \right) = 0 \Leftrightarrow 12{x^3} - 12{x^2} - 24x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 1\\x = 2\end{array} \right.\end{array}\)
BBT:
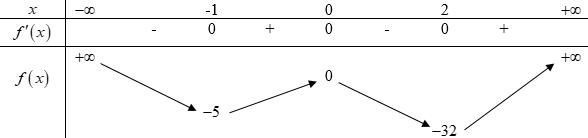
Ta có đồ thị \(y = f\left( x \right)\,\,\left( C \right)\) như sau:
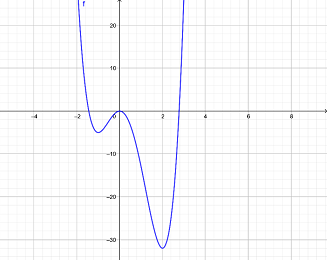
Để \(y = \left| {3{x^4} - 4{x^3} - 12{x^2} + m} \right|\) có 5 điểm cực trị thì:
TH1: \(\left( C \right)\) cắt đường thẳng \(y = - m\) tại 2 điểm phân biệt khác cực trị
\( \Leftrightarrow \left[ \begin{array}{l} - m > 0\\ - 32 < - m < - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < 0\\5 < m < 32\end{array} \right.\)
Mà \(m \in {\mathbb{Z}^ + }\, \Rightarrow m \in \left\{ {6;7;...;31} \right\}\) : 26 giá trị.
TH2: \(\left( C \right)\) cắt đường thẳng \(y = - m\) tại 3 điểm phân biệt, trong đó có 1 cực trị
\( \Leftrightarrow \left[ \begin{array}{l} - m = 0\\ - m = - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\,(L)\\m = 5\,(TM)\end{array} \right.\)
Vậy, có tất cả 27 giá trị của m thỏa mãn.
Cho hàm số \(y = f\left( x \right) = {2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018\) có đồ thị cắt trục hoành tại ba điểm phân biệt có hoành độ \({x_1};{x_2};{x_3}\). Tính giá trị biểu thức \(P = \dfrac{1}{{f'\left( {{x_1}} \right)}} + \dfrac{1}{{f'\left( {{x_2}} \right)}} + \dfrac{1}{{f'\left( {{x_3}} \right)}}.\)
Ta có \(f\left( x \right) = {2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018\)
\( \Rightarrow f'\left( x \right) = {3.2^{2019}}{x^2} + {3.2^{2019}}x = {3.2^{2019}}x\left( {x + 1} \right)\) \( \Rightarrow \dfrac{1}{{f'\left( x \right)}} = \dfrac{1}{{{{3.2}^{2019}}}}.\dfrac{1}{{x.\left( {x + 1} \right)}} = \dfrac{1}{{{{3.2}^{2019}}}}\left( {\dfrac{1}{x} - \dfrac{1}{{x + 1}}} \right)\)
Xét phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành \({2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018 = 0\) (*)
Vì \({x_1},{x_2},{x_3}\) là ba ngiệm của phương trình (*) nên theo hẹ thức Vi-et ta có
\(\left\{ \begin{array}{l}{x_1} + {x_2} + {x_3} = \dfrac{{ - 3}}{2}\\{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3} = 0\\{x_1}{x_2}{x_3} = \dfrac{{2018}}{{{2^{2019}}}}\end{array} \right.\)
Ta có \(P = \dfrac{1}{{f'\left( {{x_1}} \right)}} + \dfrac{1}{{f'\left( {{x_2}} \right)}} + \dfrac{1}{{f'\left( {{x_3}} \right)}} = \dfrac{1}{{{{3.2}^{2019}}}}\left( {\dfrac{1}{{{x_1}}} - \dfrac{1}{{{x_1} + 1}} + \dfrac{1}{{{x_2}}} - \dfrac{1}{{{x_2} + 1}} + \dfrac{1}{{{x_3}}} - \dfrac{1}{{{x_3} + 1}}} \right)\)
\( = \dfrac{1}{{{{3.2}^{2019}}}}\left[ {\left( {\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} + \dfrac{1}{{{x_3}}}} \right) - \left( {\dfrac{1}{{{x_1} + 1}} + \dfrac{1}{{{x_2} + 1}} + \dfrac{1}{{{x_3} + 1}}} \right)} \right]\)
\( = \dfrac{1}{{{{3.2}^{2019}}}}\left[ {\dfrac{{{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3}}}{{{x_1}{x_2}{x_3}}} - \dfrac{{\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right) + \left( {{x_1} + 1} \right)\left( {{x_3} + 1} \right) + \left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right)}}} \right]\)
\( = \dfrac{1}{{{{3.2}^{2019}}}}\left( {0 - \dfrac{{{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3} + 2\left( {{x_1} + {x_2} + {x_3}} \right) + 3}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right)}}} \right)\)
\( = \dfrac{1}{{{{3.2}^{2019}}}}.\dfrac{{0 + 2.\dfrac{{ - 3}}{2} + 3}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right)}} = 0\)
Hướng dẫn giải:
Sử dụng hệ thức Vi-et cho phương trình bậc ba \(a{x^3} + b{x^2} + cx + d = 0\,\left( {a \ne 0} \right)\) có ba nghiệm \({x_1},{x_2},{x_3}\)
\(\left\{ \begin{array}{l}{x_1} + {x_2} + {x_3} = \dfrac{{ - b}}{a}\\{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3} = \dfrac{c}{a}\\{x_1}{x_2}{x_3} = - \dfrac{d}{a}\end{array} \right.\)
Sau đó biến đổi \(f'\left( x \right)\) để tính \(P.\)
Đề thi liên quan
-
Đề kiểm tra 15 phút chương 1: Hàm số - Đề số 1
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 15 phút chương 1: Hàm số - Đề số 2
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 15 phút chương 1: Hàm số - Đề số 3
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 1 tiết chương 1: Hàm số - Đề số 1
-
25 câu hỏi
-
45 phút
-
-
Đề kiểm tra 1 tiết chương 1: Hàm số - Đề số 2
-
25 câu hỏi
-
45 phút
-

