Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình bên:
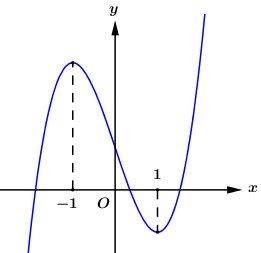
Giá trị nguyên lớn nhất của tham số m để hàm số \(y = f\left( {\left| x \right| - m} \right)\) đồng biến trên khoảng \(\left( {10; + \infty } \right)\) là:
A.
\(-10\)
B.
\(10\)
C.
\(9\)
D.
\(-11\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: c
Ta có \(y = f\left( {\left| x \right| - m} \right) = f\left( {\sqrt {{x^2}} - m} \right)\).
\( \Rightarrow y' = \dfrac{{2x}}{{2\sqrt {{x^2}} }}f'\left( {\sqrt {x^2} - m } \right) = \dfrac{x}{{\sqrt {{x^2}} }}f'\left( {\sqrt {x^2} - m } \right)\).
Để hàm số đồng biến trên \(\left( {10; + \infty } \right)\) thì \(y' \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\).
\( \Rightarrow \dfrac{x}{{\sqrt {x^2} }}f'\left( {\sqrt {x^2} - m } \right) \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\) \( \Rightarrow f'\left( {\sqrt {x^2} - m} \right) \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\,\,\left( * \right)\).
Dựa vào đồ thị hàm số ta thấy hàm số đồng biến trên \(\left( {1; + \infty } \right)\) và \(\left( { - \infty ; - 1} \right)\).
Do đó \(\left( * \right) \Leftrightarrow \left[ \begin{array}{l}\sqrt {{x^2}} - m \ge 1\,\,\forall x \in \left( {10; + \infty } \right)\,\,\,\,\,\,\left( 1 \right)\\\sqrt {{x^2}} - m \le - 1\,\,\forall x \in \left( {10; + \infty } \right)\,\,\,\left( 2 \right)\end{array} \right.\)
Xét (1) ta có \(m \le \sqrt {{x^2}} - 1\,\,\forall x \in \left( {10; + \infty } \right) \Rightarrow m \le \mathop {\min }\limits_{\left[ {10; + \infty } \right)} \left( {\sqrt {{x^2}} - 1} \right)\).
Xét \(g\left( x \right) = \sqrt {{x^2}} - 1\) trên khoảng \(\left( {10; + \infty } \right)\) ta có \(g'\left( x \right) = \dfrac{x}{{\sqrt {{x^2}} }} > 0\,\,\forall x \in \left( {10; + \infty } \right)\), do đó hàm số đồng biến trên \(\left( {10; + \infty } \right)\) \( \Rightarrow \mathop {\min }\limits_{\left[ {10; + \infty } \right)} \left( {\sqrt {{x^2}} - 1} \right) = g\left( {10} \right) = 9 \Leftrightarrow m \le 9\).
Xét (2) ta có: \(m \ge \sqrt {{x^2}} + 1\,\,\forall x \in \left( {10; + \infty } \right)\) \( \Rightarrow m \ge \mathop {\max }\limits_{\left[ {10; + \infty } \right)} \left( {\sqrt {{x^2}} + 1} \right)\).
Do \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2}} + 1} \right) = + \infty \) nên hàm số đã cho không có GTLN trên \(\left[ {10; + \infty } \right)\), do đó không tồn tại m thỏa mãn (2).
Vậy \(m \le 9\) nên giá trị nguyên lớn nhất của m bằng 9.
Hướng dẫn giải:
- Biến đổi \(f\left( {\left| x \right| - m} \right) = f\left( {\sqrt {{x^2}} - m} \right)\).
- Tính đạo hàm của hàm số.
- Để hàm số đồng biến trên \(\left( {10; + \infty } \right)\) thì \(y' \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\).
- Dựa vào BBT xác định các khoảng đồng biến của hàm số.
- Sử dụng phương pháp cô lập m.
Giải thích thêm:
Cách 2:
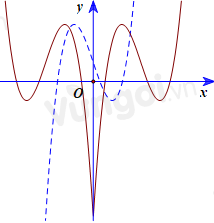
Ta vẽ đồ thị của hàm số \(y = f\left( {\left| x \right| - m} \right)\) với m>0
Tịnh tiến đồ thị hàm số \(y = f\left( x \right)\) sang phải m đơn vị, sau đó bỏ phần đồ thị của \(f\left( {x - m} \right)\) phía bên trái Oy. Lấy đối xứng phần đồ thị hàm số \(f\left( {x - m} \right)\) phía bên phải Oy qua Oy
Khi đó hàm số $f(x)$ đồng biến trên $\left( {1 ; + \infty } \right)$
=> Hàm số $y=f(x-m)$ đồng biến trên $\left( {1 +m; + \infty } \right)$
=> Hàm số $y=f(|x|-m)$ đồng biến trên $\left( {1 +m; + \infty } \right)$
Để hàm số \(y = f\left( {\left| x \right| - m} \right)\) đồng biến trên khoảng \(\left( {10; + \infty } \right)\) thì ta chỉ cần xét khoảng đồng biến của hàm số \(y = f\left( {\left| x \right| - m} \right)\) trên $\left( {1 +m; + \infty } \right)$ là được.
\(\left( {10; + \infty } \right) \subset \left( {1 + m; + \infty } \right) \Rightarrow 1 + m \le 10\)\( \Leftrightarrow m \le 9\).
Vậy giá trị nguyên lớn nhất của m là 9
Ta có \(y = f\left( {\left| x \right| - m} \right) = f\left( {\sqrt {{x^2}} - m} \right)\).
\( \Rightarrow y' = \dfrac{{2x}}{{2\sqrt {{x^2}} }}f'\left( {\sqrt {x^2} - m } \right) = \dfrac{x}{{\sqrt {{x^2}} }}f'\left( {\sqrt {x^2} - m } \right)\).
Để hàm số đồng biến trên \(\left( {10; + \infty } \right)\) thì \(y' \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\).
\( \Rightarrow \dfrac{x}{{\sqrt {x^2} }}f'\left( {\sqrt {x^2} - m } \right) \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\) \( \Rightarrow f'\left( {\sqrt {x^2} - m} \right) \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\,\,\left( * \right)\).
Dựa vào đồ thị hàm số ta thấy hàm số đồng biến trên \(\left( {1; + \infty } \right)\) và \(\left( { - \infty ; - 1} \right)\).
Do đó \(\left( * \right) \Leftrightarrow \left[ \begin{array}{l}\sqrt {{x^2}} - m \ge 1\,\,\forall x \in \left( {10; + \infty } \right)\,\,\,\,\,\,\left( 1 \right)\\\sqrt {{x^2}} - m \le - 1\,\,\forall x \in \left( {10; + \infty } \right)\,\,\,\left( 2 \right)\end{array} \right.\)
Xét (1) ta có \(m \le \sqrt {{x^2}} - 1\,\,\forall x \in \left( {10; + \infty } \right) \Rightarrow m \le \mathop {\min }\limits_{\left[ {10; + \infty } \right)} \left( {\sqrt {{x^2}} - 1} \right)\).
Xét \(g\left( x \right) = \sqrt {{x^2}} - 1\) trên khoảng \(\left( {10; + \infty } \right)\) ta có \(g'\left( x \right) = \dfrac{x}{{\sqrt {{x^2}} }} > 0\,\,\forall x \in \left( {10; + \infty } \right)\), do đó hàm số đồng biến trên \(\left( {10; + \infty } \right)\) \( \Rightarrow \mathop {\min }\limits_{\left[ {10; + \infty } \right)} \left( {\sqrt {{x^2}} - 1} \right) = g\left( {10} \right) = 9 \Leftrightarrow m \le 9\).
Xét (2) ta có: \(m \ge \sqrt {{x^2}} + 1\,\,\forall x \in \left( {10; + \infty } \right)\) \( \Rightarrow m \ge \mathop {\max }\limits_{\left[ {10; + \infty } \right)} \left( {\sqrt {{x^2}} + 1} \right)\).
Do \(\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2}} + 1} \right) = + \infty \) nên hàm số đã cho không có GTLN trên \(\left[ {10; + \infty } \right)\), do đó không tồn tại m thỏa mãn (2).
Vậy \(m \le 9\) nên giá trị nguyên lớn nhất của m bằng 9.
Hướng dẫn giải:
- Biến đổi \(f\left( {\left| x \right| - m} \right) = f\left( {\sqrt {{x^2}} - m} \right)\).
- Tính đạo hàm của hàm số.
- Để hàm số đồng biến trên \(\left( {10; + \infty } \right)\) thì \(y' \ge 0\,\,\forall x \in \left( {10; + \infty } \right)\).
- Dựa vào BBT xác định các khoảng đồng biến của hàm số.
- Sử dụng phương pháp cô lập m.
Giải thích thêm:
Cách 2:

Ta vẽ đồ thị của hàm số \(y = f\left( {\left| x \right| - m} \right)\) với m>0
Tịnh tiến đồ thị hàm số \(y = f\left( x \right)\) sang phải m đơn vị, sau đó bỏ phần đồ thị của \(f\left( {x - m} \right)\) phía bên trái Oy. Lấy đối xứng phần đồ thị hàm số \(f\left( {x - m} \right)\) phía bên phải Oy qua Oy
Khi đó hàm số $f(x)$ đồng biến trên $\left( {1 ; + \infty } \right)$
=> Hàm số $y=f(x-m)$ đồng biến trên $\left( {1 +m; + \infty } \right)$
=> Hàm số $y=f(|x|-m)$ đồng biến trên $\left( {1 +m; + \infty } \right)$
Để hàm số \(y = f\left( {\left| x \right| - m} \right)\) đồng biến trên khoảng \(\left( {10; + \infty } \right)\) thì ta chỉ cần xét khoảng đồng biến của hàm số \(y = f\left( {\left| x \right| - m} \right)\) trên $\left( {1 +m; + \infty } \right)$ là được.
\(\left( {10; + \infty } \right) \subset \left( {1 + m; + \infty } \right) \Rightarrow 1 + m \le 10\)\( \Leftrightarrow m \le 9\).
Vậy giá trị nguyên lớn nhất của m là 9
CÂU HỎI CÙNG CHỦ ĐỀ
Nếu $\mathop {\lim }\limits_{x \to x_0^ + } y = + \infty $ thì đường thẳng $x = {x_0}$ là:
Tập xác định của hàm số $y = - \dfrac{1}{2}{x^3} + 2x - 1$ là:
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số \(y = \left| {3{x^4} - 4{x^3} - 12{x^2} + m} \right|\) có 5 điểm cực trị?
Giá trị lớn nhất của hàm số $f\left( x \right) = \dfrac{{\sin x}}{x}$ trên đoạn $\left[ {\dfrac{\pi }{6};\dfrac{\pi }{3}} \right]$ là:
Cho hàm số \(f\left( x \right) = \dfrac{{ax - 1}}{{bx + c}}\,\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:
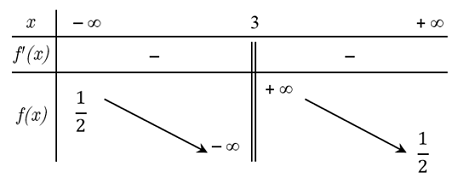
Khẳng định nào dưới đây đúng?
Đồ thị hàm số bên là đồ thị của hàm số $y = {x^4} - 4{x^2} + 1\left( C \right).$ Tìm $m$ để phương trình ${x^4} - 4{x^2} + 1 - m = 0$ có $4$ nghiệm phân biệt
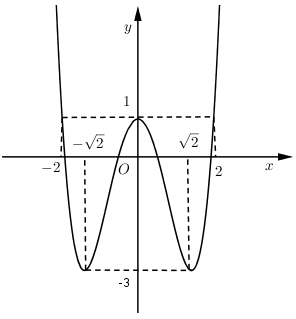
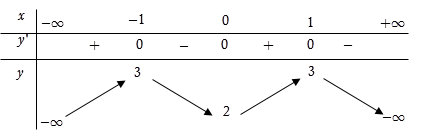
Trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số nào có bảng biến thiên như sau?
Số điểm cực trị của hàm số $y = {(x - 1)^{2017}}$ là
Cho hàm số $f\left( x \right)$ xác định và có đạo hàm trên $\left( {a;b} \right)$. Nếu $f'\left( x \right) < 0,\forall x \in \left( {a;b} \right)$ thì:
Tiếp tuyến của đồ thị hàm số \(y = \dfrac{{4x - 3}}{{2x + 1}}\) cùng với hai tiệm cận tạo thành một tam giác có diện tích bằng
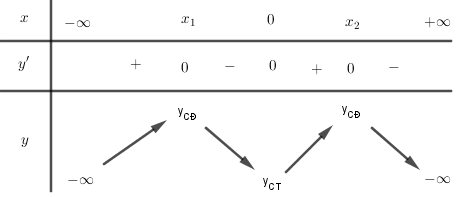
Cho hàm số $y = a{x^4} + b{x^2} + c$ có bảng biến thiên như hình vẽ. Chọn kết luận đúng:
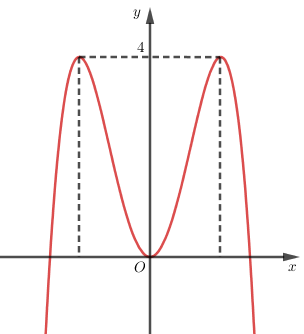
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( x \right) = {\log _2}m\) có hai nghiệm phân biệt.
Hệ số góc của tiếp tuyến của đồ thị hàm số $y = \dfrac{{{x^4}}}{4} + \dfrac{{{x^2}}}{2} - 1$ tại điểm có hoành độ $x = - 1$ là:
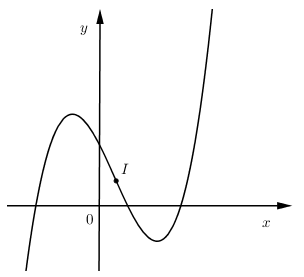
Hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ, chọn kết luận đúng:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {x^2}\left( {x - 2} \right)\left( {{x^2} - 6x + m} \right)\) với mọi \(x \in \mathbb{R}\). Có bao nhiêu số nguyên \(m\) thuộc đoạn \(\left[ { - 2019;\,2019} \right]\) để hàm số \(g\left( x \right) = f\left( {1 - x} \right)\) nghịch biến trên khoảng \(\left( { - \infty ;\, - 1} \right)\)?

