Đề kiểm tra 1 tiết chương 2: Hàm số lũy thừa, mũ và logarit - Đề số 1
-
Hocon247
-
25 câu hỏi
-
45 phút
-
632 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Tập nghiệm của bất phương trình $\ln\left[ {\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1} \right] > 0$ là:
$\begin{array}{l}\ln \left[ {\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1} \right] > 0 \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1 > 1\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) > 0\end{array}$
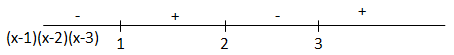
$ \Rightarrow x \in (1;2) \cup (3; + \infty )$
Hướng dẫn giải:
Tìm điều kiện để hàm $\ln f\left( x \right)$ có nghĩa là $f\left( x \right) > 0$,$\ln f(x) > 0 \Leftrightarrow f(x) > 1$ sau đó tìm $x$ .
Giải phương trình $\log_{4}\left( {x-1} \right) = 3$
Điều kiện $x \ge 1$
${\log _4}\left( {x - 1} \right) = 3 \Leftrightarrow x - 1 = {4^3} \Leftrightarrow x = 65$
Hướng dẫn giải:
Phương trình logarit cơ bản luôn có nghiệm bất kể điều kiện của $x$ là gì.
Cụ thể: \({\log _a}x = m \Leftrightarrow x = {a^m}\)
Giải thích thêm:
Có thể dùng máy tính cầm tay:
Nhập vào máy tính biểu thức log4(x – 1) – 3, dùng lệnh CALC với lần lượt 4 đáp án cho đến khi ra kết quả là 0.
Chọn B.
Trong các phương trình sau đây, phương trình nào có nghiệm?
Ý A: Điều kiện $x > 0$. Có ${x^{\frac{2}{3}}} + 5 > 0,\forall x > 0$ nên phương trình vô nghiệm
Ý B: Điều kiện $x > 4$. Có ${\left( {3x} \right)^{\frac{1}{3}}} + {\left( {x - 4} \right)^{\frac{2}{3}}} > 0,\forall x > 4$ nên phương trình vô nghiệm
Ý C: Điều kiện $x \ge 2$. Có $\sqrt {4x - 8} + 2 > 0,\forall x \ge 2$ nên phương trình vô nghiệm
Ý D: Điều kiện $x > 0$. Có $2{x^{\frac{1}{2}}} - 3 = 0 \Leftrightarrow {x^{\frac{1}{2}}} = \dfrac{3}{2} \Leftrightarrow x = {\log _{\frac{1}{2}}}\dfrac{3}{2}$ (thỏa mãn)
Hướng dẫn giải:
Giải từng phương trình tìm nghiệm và kết luận.
Kết luận nào đúng về số thực \(a\) nếu \({\left( {\dfrac{1}{a}} \right)^{ - 0,2}} < {a^2}\)
\({\left( {\dfrac{1}{a}} \right)^{ - 0,2}} < {a^2} \Leftrightarrow {a^{0,2}} < {a^2}\)
Do \(0,2 < 2\) và có số mũ không nguyên nên ${a^{0,2}} < {a^2}$ khi $a > 1$.
Hướng dẫn giải:
Sử dụng so sánh lũy thừa:
+ Với \(a > 1\) thì \({a^m} > {a^n} \Leftrightarrow m > n\)
+ Với \(0 < a < 1\) thì \({a^m} > {a^n} \Leftrightarrow m < n\)
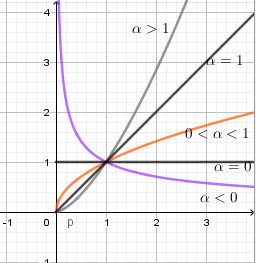
Xét hàm số \(y = {x^\alpha }\) trên tập \(\left( {0; + \infty } \right)\) có đồ thị dưới đây, chọn kết luận đúng:

Từ hình vẽ ta thấy \(1 < {2^\alpha } < 2 \Rightarrow 0 < \alpha < 1\)
.
Hướng dẫn giải:
Sử dụng các dáng đồ thị hàm số \(y = {x^\alpha }\) ứng với các điều kiện khác nhau của \(\alpha \):
Giải thích thêm:
Nhiều HS sẽ sử dụng tính đồng biến nghịch biến để xét, vì thấy hàm số đồng biến nên vội vàng kết luận \(\alpha > 1\) vì nhầm với tính đơn điệu của hàm số mũ là sai.
Có thể nhận xét trực tiếp:
Đồ thị là đường cong nên loại A và B.
Mặt khác thấy $x=4$ thì $y = 2$ nên chọn D
Cho các số thực \(a < b < 0\). Mệnh đề nào sau đây sai?
Do $a < b < 0$ nên đáp án B viết $\ln a, \ln b$ là sai.
Hướng dẫn giải:
Sử dụng công thức:
$\begin{array}{l}{\log _a}xy = {\log _a}x + {\log _a}y \Rightarrow \ln xy = \ln x + \ln y\,\left( {x,y > 0} \right)\\{\log _a}\dfrac{x}{y} = {\log _a}x - {\log _a}y \Rightarrow \ln \dfrac{x}{y} = \ln x - \ln y\left( {x,y > 0} \right)\\{\log _a}{b^n} = n.{\log _a}b(b > 0) \Rightarrow ln{b^n} = n\ln b(b > 0)\end{array}$
Công thức nào sau đây là công thức tăng trưởng mũ?
Công thức lãi kép (hoặc công thức tăng trưởng mũ):
\(T = A.{e^{Nr}}\), ở đó \(A\) là số tiền gửi ban đầu, \(r\) là lãi suất, \(N\) là số kì hạn.
Tìm tập nghiệm của phương trình \({\log _3}x + \dfrac{1}{{{{\log }_9}x}} = 3\)
Điều kiện: \(x > 0;x \ne 1\)
${\log _3}x + \dfrac{1}{{{{\log }_9}x}} = 3 \Leftrightarrow {\log _3}x + \dfrac{2}{{{{\log }_3}x}} = 3 \Leftrightarrow {\left( {{{\log }_3}x} \right)^2} - 3{\log _3}x + 2 = 0$
\( \Leftrightarrow \left[ \begin{array}{l}{\log _3}x = 1\\{\log _3}x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = {3^2} = 9\end{array} \right.\)
Hướng dẫn giải:
Giải phương trình logarit:
+ Đặt điều kiện cho phương trình
+ Biến đổi phương trình đưa về cùng cơ số
Nếu $a > 1$ và $b > c > 0$ thì:
Nếu $a > 1$ và $b > c > 0$ thì ${\log _a}b > {\log _a}c$.
Hướng dẫn giải:
Sử dụng tính chất: Nếu $a > 1;b,c > 0$ thì ${\log _a}b > {\log _a}c \Leftrightarrow b > c$.
Cho các đồ thị hàm số \(y = {a^x},y = {b^x},y = {c^x}\left( {0 < a,b,c \ne 1} \right)\), chọn khẳng định đúng:
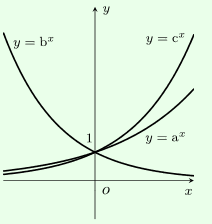
Ta thấy:
- Hàm số \(y = {b^x}\) nghịch biến nên \(0 < b < 1\).
- Hàm số \(y = {a^x},y = {c^x}\) đồng biến nên \(a,c > 1 > b\), loại B và D.
- Xét phần đồ thị hai hàm số \(y = {a^x},y = {c^x}\) ta thấy phần đồ thị hàm số \(y = {c^x}\) nằm trên đồ thị hàm số \(y = {a^x}\) nên \({c^x} > {a^x},\forall x > 0 \Leftrightarrow c > a\).
Hướng dẫn giải:
- Bước 1: Quan sát các đồ thị, nhận xét về tính đơn điệu để nhận xét các cơ số.
+ Hàm số đồng biến thì cơ số lớn hơn \(1\).
+ Hàm số nghịch biến thì cơ số lớn hơn \(0\) và nhỏ hơn \(1\).
- Bước 2: So sánh các cơ số dựa vào phần đồ thị của hàm số.
- Bước 3: Kết hợp các điều kiện ở trên ta được mối quan hệ cần tìm.
Giải thích thêm:
Nhiều HS không xét đến tính đồng biến nghịch biến nên thấy đồ thị hàm số \(y = {a^x}\) nằm phía dưới chọn ngay đáp án B là sai, một số em khác chọn sai đáp án C vì không xét được hai đồ thị hàm số \(y = {a^x},y = {c^x}\).
Viết các số sau theo thứ tự tăng dần: $a = {1^{3,8}};\,\,b = {2^{ - 1}};\,\,c = {\left( {\dfrac{1}{2}} \right)^{ - 3}}$
Ta có: $a = {1^{3,8}} = 1$; $b = {2^{ - 1}} = \dfrac{1}{2} = 0,5$ và $c = {\left( {\dfrac{1}{2}} \right)^{ - 3}} = {2^3} = 8.$
Mà $0,5 < 1 < 8 \Rightarrow b < a < c$
Hướng dẫn giải:
Tính giá trị các số $a,b,c$ và so sánh.
Giải thích thêm:
HS thường tính nhầm giá trị $c = \dfrac{1}{8}$ dẫn đến chọn nhầm đáp án C là sai.
Một số em lại tính nhầm $1^{3,8}=3,8$ hay $2^{-1}=-2$ và chọn sai đáp án.
Chọn mệnh đề đúng:
Giới hạn cần nhớ: \(\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln \left( {1 + x} \right)}}{x} = 1\)
Chọn đẳng thức đúng:
Áp dụng công thức ${\log _a}b = \dfrac{1}{{{{\log }_b}a}} \Leftrightarrow {\log _a}b.{\log _b}a = 1\left( {0 < a,b \ne 1} \right)$ ta được:
${\log _2}3 = \dfrac{1}{{{{\log }_3}2}}$ nên D đúng.
Hướng dẫn giải:
Sử dụng công thức ${\log _a}b = \dfrac{1}{{{{\log }_b}a}} \Leftrightarrow {\log _a}b.{\log _b}a = 1\left( {0 < a,b \ne 1} \right)$
Giải thích thêm:
HS thường chọn nhầm đáp án A vì nghĩ rằng ${\log _2}3 + {\log _3}2 = 0$ là sai.
Tìm tập nghiệm S của bất phương trình \({5^{x + 1}} - \dfrac{1}{5} > 0\)
Ta có: ${5^{x + 1}} - \dfrac{1}{5} > 0 \Leftrightarrow {5^{x + 1}} > \dfrac{1}{5} = {5^{ - 1}} \Leftrightarrow x + 1 > - 1 \Leftrightarrow x > - 2$
Hướng dẫn giải:
Sử dụng cách giải về bất phương trình mũ, đưa bất phương trình về cùng cơ số 5. Sau đó sử dụng công thức: ${a^{f(x)}} > {a^{g(x)}} \Leftrightarrow f(x) > g(x),(a > 1)$
Giải thích thêm:
Nhiều HS sẽ giải như sau:
${5^{x + 1}} - \dfrac{1}{5} > 0 \Leftrightarrow {5^{x + 1}} > \dfrac{1}{5} = {5^{ - 1}} \Leftrightarrow x + 1 < - 1 \Leftrightarrow x < - 2$ và chọn D là sai vì cơ số \(5 > 1\).
Giá trị $P = \dfrac{{\sqrt[5]{4}.\sqrt[4]{{64}}.{{(\sqrt[3]{{\sqrt 2 }})}^4}}}{{\sqrt[3]{{\sqrt[3]{{32}}}}}}$ là:
$P = \dfrac{{\sqrt[5]{4}.\sqrt[4]{{64}}.{{(\sqrt[3]{{\sqrt 2 }})}^4}}}{{\sqrt[3]{{\sqrt[3]{{32}}}}}} = \dfrac{{{2^{\frac{2}{5}}}{{.2}^{\frac{6}{4}}}{{.2}^{\frac{4}{6}}}}}{{{2^{\frac{5}{9}}}}} = {2^{\frac{2}{5} + \frac{6}{4} + \frac{4}{6} - \frac{5}{9}}} = {2^{\frac{{181}}{{90}}}}$
Vậy \(P = {2^{\frac{{181}}{{90}}}}.\)
Hướng dẫn giải:
Sử dụng các tính chất \({a^{\dfrac{m}{n}}} = \sqrt[n]{{{a^m}}};\sqrt[m]{{\sqrt[n]{a}}} = \sqrt[{mn}]{a}\) để biến đổi và rút gọn \(P\).
Giải thích thêm:
Hs có thể sai lầm khi dùng công thức \(\sqrt[m]{{\sqrt[n]{a}}} = {a^{m.n}}\) hoặc \(\sqrt[m]{{\sqrt[n]{a}}} = {a^{\frac{m}{n}}}\) là sai.
Tìm TXĐ của hàm số \(y = {\left( {{x^3} - 27} \right)^{\dfrac{\pi }{2}}}\)
Hàm số \(y = {\left( {{x^3} - 27} \right)^{\dfrac{\pi }{2}}}\) xác định khi \({x^3} - 27 > 0 \Leftrightarrow x > 3\).
Hướng dẫn giải:
Sử dụng lý thuyết: Lũy thừa với số mũ không nguyên thì cơ số phải dương.
Giải thích thêm:
Nhiều em HS sẽ chọn đáp án C vì không nhớ rõ điều kiện xác định của hàm số.
Với \(a\) và \(b\) là hai số thực dương tùy ý, \(\log \left( {a{b^2}} \right)\) bằng
Ta có: \(\log \left( {a{b^2}} \right) = \log a + \log {b^2} = \log a + 2\log b\)
Hướng dẫn giải:
Sử dụng các công thức biến đổi logarit: \(\log \left( {xy} \right) = \log x + \log y;\;\;\log {x^n} = n\log x\) với \(x;y\) là các số thực dương.
Sự tăng trưởng của 1 loài vi khuẩn được tính theo công thức $S = A.{e^{rt}}$ , trong đó $A$ là số lượng vi khuẩn ban đầu, $r$ là tỉ lệ tăng trưởng $(r>0)$, $t$ là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là $150$ con và sau $5$ giờ có $450$ con, tìm số lượng vi khuẩn sau 10 giờ tăng trưởng.
Ta có: $450 = 150.{e^{5r}}$
$ = > {e^{5r}} = 3 \Leftrightarrow 5r = \ln 3 = > r = \dfrac{{\ln 3}}{5}$
Số lượng vi khuẩn sau 10 giờ tăng trưởng là:
$S = 150.{e^{10.\dfrac{{\ln 3}}{5}}} = 150.{\left( {{e^{\ln 3}}} \right)^2} = {150.3^2} = 1350$(con)
Hướng dẫn giải:
- Tính tỉ lệ tăng trưởng \(r\).
- Sử dụng công thức $S = A.{e^{rt}}$ để tính số lượng vi khuẩn.
Cho hàm số \(y = {3^x} + \ln 3\). Chọn mệnh đề đúng:
Ta có: \(y = {3^x} + \ln 3 \Rightarrow y' = {3^x}\ln 3\)
Lại có: \(y = {3^x} + \ln 3 \Rightarrow {3^x} = y - \ln 3 \Rightarrow y' = \left( {y - \ln 3} \right)\ln 3 = y\ln 3 - {\ln ^2}3\)
Hướng dẫn giải:
Áp dụng công thức tính đạo hàm hàm số mũ \(y = {a^x} \Rightarrow y' = {a^x}\ln a\).
Giải thích thêm:
Nhiều HS thường nhớ sai công thức \(\left( {{a^x}} \right)' = {a^x}\) dẫn đến chọn nhầm đáp án D là sai.
Biết hai hàm số $y = {a^x}$ và $y = f\left( x \right)$ có đồ thị như hình vẽ đồng thời đồ thị của hai hàm số này đối xứng nhau qua đường thẳng $d:y = - x$. Tính $f\left( { - {a^3}} \right).$

Giả sử \(M\left( {{x_M};{y_M}} \right)\) là điểm thuộc hàm số \(y = {a^x}\); \(N\left( {{x_0};{y_0}} \right)\) là điểm đối xứng của \(M\) qua đường thẳng \(y = - x\).
Gọi \(I\) là trung điểm của \(MN \Rightarrow I\left( {\dfrac{{{x_M} + {x_0}}}{2};\dfrac{{{y_M} + {y_0}}}{2}} \right)\).
Vì \(M,{\rm{ }}N\) đối xứng nhau qua $d$ $ \Rightarrow \left\{ \begin{array}{l}I \in d\\\overrightarrow {MN} //\overrightarrow {{n_d}} \end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{{y_M} + {y_0}}}{2} = - \dfrac{{{x_M} + {x_0}}}{2}\\\dfrac{{{x_M} - {x_0}}}{1} = \dfrac{{{y_M} - {y_0}}}{1}\end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l}{x_0} = - {y_M}\\{y_0} = - {x_M}\end{array} \right.$
Ta có \(M\left( {{x_M};{y_M}} \right) \in \) đồ thị \(y = {a^x}\) nên \({y_M} = {a^{{x_M}}}\).
Do đó ${x_0} = - {y_M} = - {a^{{x_M}}} = - {a^{ - {y_0}}}$$ \Rightarrow - {y_0} = {\log _a}\left( { - {x_0}} \right) \Leftrightarrow {y_0} = - {\log _a}\left( { - {x_0}} \right)$.
Điều này chứng tỏ điểm \(N\) thuộc đồ thị hàm số $f\left( x \right) = - {\log _a}\left( { - x} \right)$.
Khi đó \(f\left( { - {a^3}} \right) = - {\log _a}{a^3} = - 3.\)
Hướng dẫn giải:
- Tìm hàm số \(y = f\left( x \right)\).
- Tính giá trị \(f\left( { - {a^3}} \right)\) theo công thức vừa tìm được ở trên.
Giải thích thêm:
Cách 2. Lấy đối xứng đồ thị hàm số \(y = {a^x}\) qua \(Oy\) là được đồ thị hàm số \(y = {a^{ - x}} = {\left( {\dfrac{1}{a}} \right)^x}.\)
Lấy đối xứng đồ thị hàm số \(y = f\left( x \right)\) qua \(Oy\) là được đồ thị hàm số \(y = f\left( { - x} \right).\)
Theo giả thiết, ta có đồ thị hai hàm số \(y = {a^x}\) và \(y = f\left( x \right)\) đối xứng nhau qua đường thẳng \(y = - x\) nên suy ra đồ thị của hai hàm số \(y = {\left( {\dfrac{1}{a}} \right)^x}\) và \(y = f\left( { - x} \right)\) đối xứng nhau qua đường thẳng \(y = x\). \(\left( 1 \right)\)
Theo lý thuyết (SGK) thì đồ thị của hai hàm số \(y = {a^x}\) và \(y = {\log _a}x\) đối xứng nhau qua đường thẳng \(y = x.\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(f\left( { - x} \right) = {\log _{\frac{1}{a}}}x \Rightarrow f\left( { - {a^3}} \right) = {\log _{\frac{1}{a}}}{a^3} = - 3.\)
Tìm các giá trị $m$ để phương trình \({2^{x + 1}} = m{.2^{x + 2}} - {2^{x + 3}}\) luôn thỏa, \(\forall x \in \mathbb{R}\).
\({2^{x + 1}} = m{.2^{x + 2}} - {2^{x + 3}}{\rm{ }} \Leftrightarrow {2^{x + 1}} = m{.2^{x + 1 + 1}} - {2^{x + 1 + 2}} \)
$\Leftrightarrow {2^{x + 1}} = m{.2.2^{x + 1}} - {2^2}{.2^{x + 1}} \Leftrightarrow {2^{x + 1}} = (2m - 4){2^{x + 1}}$
\( \Leftrightarrow 2m - 4 = 1 \Leftrightarrow m = \dfrac{5}{2}\)
Hướng dẫn giải:
Sử dụng phương pháp đồng nhất hệ số.
Tìm số nghiệm nguyên của bất phương trình \({\left( {\dfrac{1}{5}} \right)^{{x^2} - 2x}} \ge \dfrac{1}{{125}}\)
Ta có
${\left( {\dfrac{1}{5}} \right)^{{x^2} - 2{\rm{x}}}} \ge \dfrac{1}{{125}} \Leftrightarrow {\left( {\dfrac{1}{5}} \right)^{{x^2} - 2{\rm{x}}}} \ge {\left( {\dfrac{1}{5}} \right)^3} $
$\Leftrightarrow {x^2} - 2{\rm{x}} \le 3 \Leftrightarrow {x^2} - 2{\rm{x - 3}} \le {\rm{0}} \Leftrightarrow {\rm{ - 1}} \le {\rm{x}} \le {\rm{3}}$
Số nghiệm nguyên là $5$.
Hướng dẫn giải:
Giải bất phương trình mũ với \(0 < a < 1\) thì ${a^{f\left( x \right)}} \ge {a^{g\left( x \right)}} \Leftrightarrow f\left( x \right) \le g\left( x \right)$
Giải thích thêm:
Nhiều HS sẽ có lập luận như sau: ${\left( {\dfrac{1}{5}} \right)^{{x^2} - 2{\rm{x}}}} \ge \dfrac{1}{{125}} \Leftrightarrow {\left( {\dfrac{1}{5}} \right)^{{x^2} - 2{\rm{x}}}} \ge {\left( {\dfrac{1}{5}} \right)^3} \Leftrightarrow {x^2} - 2{\rm{x}} \ge 3$ là sai vì \(0 < \dfrac{1}{5} < 1\)
Tập nghiệm của bất phương trình $({2^{{x^2} - 4}} - 1).\ln {x^2} < 0$ là:
Điều kiện: \(x \ne 0\).
\(\begin{array}{l}({2^{{x^2} - 4}} - 1) \ln{x^2} < 0 \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}({2^{{x^2} - 4}} - 1) > 0\\ \ln{x^2} < 0\end{array} \right.\\\left\{ \begin{array}{l}({2^{{x^2} - 4}} - 1) < 0\\ \ln{x^2} > 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{2^{{x^2} - 4}} > 1\\{x^2} < 1\end{array} \right.\\\left\{ \begin{array}{l}{2^{{x^2} - 4}} < 1\\{x^2} > 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{x^2} - 4 > 0\\{x^2} < 1\end{array} \right.\\\left\{ \begin{array}{l}{x^2} - 4 < 0\\{x^2} > 1\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 2;x < - 2\\ - 1 < x < 1\end{array} \right.\\\left\{ \begin{array}{l} - 2 < x < 2\\x > 1;x < - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - 2 < x < - 1\\1 < x < 2\end{array} \right. \Rightarrow x \in \left( { - 2; - 1} \right) \cup \left( {1;2} \right)\end{array}\)
Hướng dẫn giải:
Sử dụng phương pháp giải bất phương trình mũ và bất phương trình logarit.
Bà Hoa gửi $100$ triệu vào tài khoản định kì tính lãi suất là $8\% $ một năm. Sau 5 năm, bà rút toàn bộ số tiền và dùng một nửa để sửa nhà, còn một nửa tiền bà lại đem gửi ngân hàng trong 5 năm với cùng lãi suất. Tính số tiền lãi thu được sau 10 năm.
Số tiền bà Hoa rút sau 5 năm đầu là: $100{\left( {1 + 8\% } \right)^5} = 146,932$ triệu.
Số tiền lãi lần 1 là: $146,932 - 100 = 46,932$ triệu.
Số tiền bà gửi tiếp vào ngân hàng là: $146,932:2 = 73,466$ triệu
Số tiền và có sau 5 năm là: $73,466{\left( {1 + 8\% } \right)^5} = 107,946$ triệu.
Số tiền lãi lần 2 là: $107,946 - 73,466 = 34,480$ triệu.
Tổng số tiền lãi sau 2 lần là: $46,932 + 34,480 = 81,412$ triệu.
Hướng dẫn giải:
- Tính số tiền bà Hoa rút ra sau 5 năm theo công thức $T = A{\left( {1 + r} \right)^N}$.
- Tính số tiền lãi lần đầu.
- Tính số tiền bà đem gửi lần 2.
- Tính số tiền sau 5 năm lần 2 theo công thức: $T = A{\left( {1 + r} \right)^N}$
- Tính số tiền lãi lần 2 và suy ra đáp số.
Gọi $m$ là số chữ số cần dùng khi viết số $2^{30}$ trong hệ thập phân và $n$ là số chữ số cần dùng khi viết số $30^2$ trong hệ nhị phân. Ta có tổng $m + n$ bằng
Dựa vào 2 kết quả trên ta có
$\begin{array}{l}m = \left[ {\log {2^{30}}} \right] + 1 = \left[ {30\log 2} \right] + 1 = 10\\n = \left[ {{{\log }_2}{{30}^2}} \right] + 1 = \left[ {2{{\log }_2}30} \right] + 1 = 10\\ \Rightarrow m + n = 20\end{array}$
Hướng dẫn giải:
Số chữ số cần dùng khi viết số $A$ trong hệ thập phân là $[\log A] + 1$ với $[x]$ là số nguyên lớn nhất nhỏ hơn hoặc bằng $x$
Tổng quát: số chữ số cần dùng khi viết số $A$ trong hệ $n–$phân là $[\log _{n} A] + 1$
Đề thi liên quan
-
Đề kiểm tra 15 phút chương 2: Hàm số lũy thừa, mũ, logarit - Đề số 1
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 15 phút chương 2: Hàm số lũy thừa, mũ, logarit - Đề số 2
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 15 phút chương 2: Hàm số lũy thừa, mũ, logarit - Đề số 3
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 1 tiết chương 2: Hàm số lũy thừa, mũ và logarit - Đề số 2
-
25 câu hỏi
-
45 phút
-
-
Đề kiểm tra 1 tiết chương 2: Hàm số lũy thừa, mũ và logarit - Đề số 3
-
25 câu hỏi
-
45 phút
-

