Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: d
Hàm số \(y = {\left( {{x^3} - 27} \right)^{\dfrac{\pi }{2}}}\) xác định khi \({x^3} - 27 > 0 \Leftrightarrow x > 3\).
Hướng dẫn giải:
Sử dụng lý thuyết: Lũy thừa với số mũ không nguyên thì cơ số phải dương.
Giải thích thêm:
Nhiều em HS sẽ chọn đáp án C vì không nhớ rõ điều kiện xác định của hàm số.
Hàm số \(y = {\left( {{x^3} - 27} \right)^{\dfrac{\pi }{2}}}\) xác định khi \({x^3} - 27 > 0 \Leftrightarrow x > 3\).
Hướng dẫn giải:
Sử dụng lý thuyết: Lũy thừa với số mũ không nguyên thì cơ số phải dương.
Giải thích thêm:
Nhiều em HS sẽ chọn đáp án C vì không nhớ rõ điều kiện xác định của hàm số.
CÂU HỎI CÙNG CHỦ ĐỀ
Tập nghiệm của bất phương trình $\ln\left[ {\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1} \right] > 0$ là:
Viết các số sau theo thứ tự tăng dần: $a = {1^{3,8}};\,\,b = {2^{ - 1}};\,\,c = {\left( {\dfrac{1}{2}} \right)^{ - 3}}$
Giá trị $P = \dfrac{{\sqrt[5]{4}.\sqrt[4]{{64}}.{{(\sqrt[3]{{\sqrt 2 }})}^4}}}{{\sqrt[3]{{\sqrt[3]{{32}}}}}}$ là:
Tìm tập nghiệm của phương trình \({\log _3}x + \dfrac{1}{{{{\log }_9}x}} = 3\)
Sự tăng trưởng của 1 loài vi khuẩn được tính theo công thức $S = A.{e^{rt}}$ , trong đó $A$ là số lượng vi khuẩn ban đầu, $r$ là tỉ lệ tăng trưởng $(r>0)$, $t$ là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là $150$ con và sau $5$ giờ có $450$ con, tìm số lượng vi khuẩn sau 10 giờ tăng trưởng.
Trong các phương trình sau đây, phương trình nào có nghiệm?
Với \(a\) và \(b\) là hai số thực dương tùy ý, \(\log \left( {a{b^2}} \right)\) bằng
Gọi $m$ là số chữ số cần dùng khi viết số $2^{30}$ trong hệ thập phân và $n$ là số chữ số cần dùng khi viết số $30^2$ trong hệ nhị phân. Ta có tổng $m + n$ bằng
Xét hàm số \(y = {x^\alpha }\) trên tập \(\left( {0; + \infty } \right)\) có đồ thị dưới đây, chọn kết luận đúng:

Tập nghiệm của bất phương trình $({2^{{x^2} - 4}} - 1).\ln {x^2} < 0$ là:
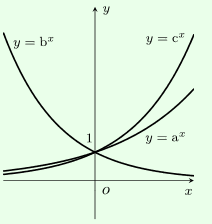
Cho các đồ thị hàm số \(y = {a^x},y = {b^x},y = {c^x}\left( {0 < a,b,c \ne 1} \right)\), chọn khẳng định đúng:
Tìm số nghiệm nguyên của bất phương trình \({\left( {\dfrac{1}{5}} \right)^{{x^2} - 2x}} \ge \dfrac{1}{{125}}\)
Cho các số thực \(a < b < 0\). Mệnh đề nào sau đây sai?

