Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: a
$P = \dfrac{{\sqrt[5]{4}.\sqrt[4]{{64}}.{{(\sqrt[3]{{\sqrt 2 }})}^4}}}{{\sqrt[3]{{\sqrt[3]{{32}}}}}} = \dfrac{{{2^{\frac{2}{5}}}{{.2}^{\frac{6}{4}}}{{.2}^{\frac{4}{6}}}}}{{{2^{\frac{5}{9}}}}} = {2^{\frac{2}{5} + \frac{6}{4} + \frac{4}{6} - \frac{5}{9}}} = {2^{\frac{{181}}{{90}}}}$
Vậy \(P = {2^{\frac{{181}}{{90}}}}.\)
Hướng dẫn giải:
Sử dụng các tính chất \({a^{\dfrac{m}{n}}} = \sqrt[n]{{{a^m}}};\sqrt[m]{{\sqrt[n]{a}}} = \sqrt[{mn}]{a}\) để biến đổi và rút gọn \(P\).
Giải thích thêm:
Hs có thể sai lầm khi dùng công thức \(\sqrt[m]{{\sqrt[n]{a}}} = {a^{m.n}}\) hoặc \(\sqrt[m]{{\sqrt[n]{a}}} = {a^{\frac{m}{n}}}\) là sai.
$P = \dfrac{{\sqrt[5]{4}.\sqrt[4]{{64}}.{{(\sqrt[3]{{\sqrt 2 }})}^4}}}{{\sqrt[3]{{\sqrt[3]{{32}}}}}} = \dfrac{{{2^{\frac{2}{5}}}{{.2}^{\frac{6}{4}}}{{.2}^{\frac{4}{6}}}}}{{{2^{\frac{5}{9}}}}} = {2^{\frac{2}{5} + \frac{6}{4} + \frac{4}{6} - \frac{5}{9}}} = {2^{\frac{{181}}{{90}}}}$
Vậy \(P = {2^{\frac{{181}}{{90}}}}.\)
Hướng dẫn giải:
Sử dụng các tính chất \({a^{\dfrac{m}{n}}} = \sqrt[n]{{{a^m}}};\sqrt[m]{{\sqrt[n]{a}}} = \sqrt[{mn}]{a}\) để biến đổi và rút gọn \(P\).
Giải thích thêm:
Hs có thể sai lầm khi dùng công thức \(\sqrt[m]{{\sqrt[n]{a}}} = {a^{m.n}}\) hoặc \(\sqrt[m]{{\sqrt[n]{a}}} = {a^{\frac{m}{n}}}\) là sai.
CÂU HỎI CÙNG CHỦ ĐỀ
Tập nghiệm của bất phương trình $\ln\left[ {\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1} \right] > 0$ là:
Viết các số sau theo thứ tự tăng dần: $a = {1^{3,8}};\,\,b = {2^{ - 1}};\,\,c = {\left( {\dfrac{1}{2}} \right)^{ - 3}}$
Tìm tập nghiệm của phương trình \({\log _3}x + \dfrac{1}{{{{\log }_9}x}} = 3\)
Sự tăng trưởng của 1 loài vi khuẩn được tính theo công thức $S = A.{e^{rt}}$ , trong đó $A$ là số lượng vi khuẩn ban đầu, $r$ là tỉ lệ tăng trưởng $(r>0)$, $t$ là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là $150$ con và sau $5$ giờ có $450$ con, tìm số lượng vi khuẩn sau 10 giờ tăng trưởng.
Gọi $m$ là số chữ số cần dùng khi viết số $2^{30}$ trong hệ thập phân và $n$ là số chữ số cần dùng khi viết số $30^2$ trong hệ nhị phân. Ta có tổng $m + n$ bằng
Trong các phương trình sau đây, phương trình nào có nghiệm?
Với \(a\) và \(b\) là hai số thực dương tùy ý, \(\log \left( {a{b^2}} \right)\) bằng
Tìm TXĐ của hàm số \(y = {\left( {{x^3} - 27} \right)^{\dfrac{\pi }{2}}}\)
Tập nghiệm của bất phương trình $({2^{{x^2} - 4}} - 1).\ln {x^2} < 0$ là:
Xét hàm số \(y = {x^\alpha }\) trên tập \(\left( {0; + \infty } \right)\) có đồ thị dưới đây, chọn kết luận đúng:

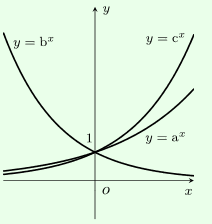
Cho các đồ thị hàm số \(y = {a^x},y = {b^x},y = {c^x}\left( {0 < a,b,c \ne 1} \right)\), chọn khẳng định đúng:
Tìm số nghiệm nguyên của bất phương trình \({\left( {\dfrac{1}{5}} \right)^{{x^2} - 2x}} \ge \dfrac{1}{{125}}\)

