Đề kiểm tra 15 phút chương 2: Hàm số lũy thừa, mũ, logarit - Đề số 2
-
Hocon247
-
12 câu hỏi
-
45 phút
-
637 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Giải phương trình \({\log _3}\left( {x + 2} \right) + {\log _9}{\left( {x + 2} \right)^2} = \dfrac{5}{4}\)
${\log _3}(x + 2) + {\log _9}{(x + 2)^2} = \dfrac{5}{4}$ (*)
Đkxđ: $x > - 2$
$(*) \Leftrightarrow {\log _3}(x + 2) + {\log _3}(x + 2) = \dfrac{5}{4} \Leftrightarrow {\log _3}(x + 2) = \dfrac{5}{8} $
$\Leftrightarrow x + 2 = {3^{\dfrac{5}{8}}} \Leftrightarrow x = \sqrt[8]{{{3^5}}} - 2(tm)$
Hướng dẫn giải:
- Bước 1: Biến đổi các logarit về cùng cơ số.
- Bước 2: Giải phương trình logarit cơ bản \({\log _a}x = m \Leftrightarrow x = {a^m}\)
- Bước 3: Kết hợp điều kiện và kết luận nghiệm.
Chọn mệnh đề đúng:
Ta có:
Hàm số $y=a^{-x}$ nghịch biến khi $a>1$ nên các đáp án B, D đều sai.
\(y = {a^{ - x}} = \dfrac{1}{{{a^x}}} = {\left( {\dfrac{1}{a}} \right)^x}\left( {0 < a \ne 1} \right)\) nên hàm số đồng biến nếu \(\dfrac{1}{a} > 1 \Leftrightarrow 0 < a < 1\).
Giải thích thêm:
Nhiều HS sẽ chọn nhầm đáp án A hoặc B vì nghĩ hàm số đó giống hàm số \(y = {a^x}\), hoặc một số em khác lại chọn đáp án D vì nghĩ \(y = {a^{ - x}}\) luôn nghịch biến. Thực chất nó chỉ nghịch biến nếu \(a > 1\).
Tìm tập nghiệm \(S\) của phương trình ${\log _6}\left[ {x\left( {5 - x} \right)} \right] = 1.$
Phương trình $ \Leftrightarrow x\left( {5 - x} \right) = 6 \Leftrightarrow {x^2} - 5x + 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 3\end{array} \right..$
Hướng dẫn giải:
Sử dụng phương pháp giải phương trình logarit cơ bản \({\log _a}x = m\left( {0 < a \ne 1} \right) \Leftrightarrow x = {a^m}\)
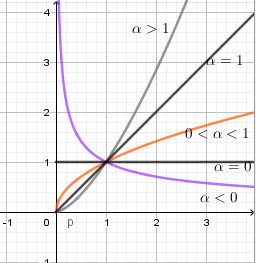
Xét hàm số \(y = {x^\alpha }\) trên tập \(\left( {0; + \infty } \right)\) có đồ thị dưới đây, chọn kết luận đúng:

Từ hình vẽ ta thấy \(1 < {2^\alpha } < 2 \Rightarrow 0 < \alpha < 1\)
.
Hướng dẫn giải:
Sử dụng các dáng đồ thị hàm số \(y = {x^\alpha }\) ứng với các điều kiện khác nhau của \(\alpha \):
Giải thích thêm:
Nhiều HS sẽ sử dụng tính đồng biến nghịch biến để xét, vì thấy hàm số đồng biến nên vội vàng kết luận \(\alpha > 1\) vì nhầm với tính đơn điệu của hàm số mũ là sai.
Có thể nhận xét trực tiếp:
Đồ thị là đường cong nên loại A và B.
Mặt khác thấy $x=4$ thì $y = 2$ nên chọn D
Tổng các nghiệm của phương trình \({3^{{x^4} - 3{x^2}}} = 81\)
\({3^{{x^4} - 3{x^2}}} = 81 = {3^4} \Leftrightarrow {x^4} - 3{x^2} - 4 = 0 \Leftrightarrow {x^2} = 4 \Leftrightarrow x = \pm 2\)
Tổng các nghiệm sẽ bằng $0$.
Hướng dẫn giải:
Đưa hai vế về dạng hai lũy thừa cùng cơ số.
Hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) có đồ thị như hình vẽ bên:
Đường thẳng \(y = 3\) cắt hai đồ thị tại các điểm có hoành độ \({x_1},\,\,{x_2}.\) Biết rằng \({x_2} = 2{x_1},\) giá trị của \(\dfrac{a}{b}\) bằng:
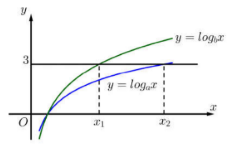
Dựa vào đồ thị hàm số ta thấy \({x_1}\) là nghiệm của phương trình hoành độ giao điểm \({\log _b}{x_1} = 3 \Leftrightarrow {x_1} = {b^3}.\)
Và \({x_2}\) là nghiệm của phương trình hoành độ giao điểm \({\log _a}{x_2} = 3 \Leftrightarrow {x_2} = {a^3}.\)
Theo đề bài ta có: \({x_2} = 2{x_1} \Rightarrow {a^3} = 2{b^3} \Leftrightarrow \dfrac{{{a^3}}}{{{b^3}}} = 2 \Leftrightarrow \dfrac{a}{b} = \sqrt[3]{2}.\)
Hướng dẫn giải:
Dựa vào đồ thị hàm số, xác định các giá trị của \({x_1},\,{x_2}\) theo \(a\) và \(b.\) Từ đó tính giá trị của \(\dfrac{a}{b}.\)
Số nghiệm của phương trình \({2^{2{x^2} - 7x + 5}} = 1\) là:
\({2^{2{x^2} - 7x + 5}} = 1 \Leftrightarrow {2^{2{x^2} - 7x + 5}} = {2^0} \Leftrightarrow 2{x^2} - 7x + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \dfrac{5}{2}\end{array} \right..\)
Vậy phương trình đã cho có 2 nghiệm
Hướng dẫn giải:
Giải phương trình mũ bằng phương pháp đưa về cùng cơ số bằng cách đưa \(1 = {2^0}.\)
Trong các hàm số sau đây, hàm số nào đồng biến trên các khoảng xác định?
Hàm số \(y = {x^{ - 4}}\) có tập xác định là \(\mathbb{R}\backslash \left\{ 0 \right\}\) và có \(y' = - 4{x^{ - 5}}\) nên không đồng biến trên các khoảng xác định (đồng biến trên \(\left( { - \infty ,0} \right)\) và nghịch biến trên \(\left( {0, + \infty } \right)\)), loại A.
Hàm số \(y = {x^{ - \dfrac{3}{4}}}\) có tập xác định là \(\left( {0, + \infty } \right)\) và có \(y' = - \dfrac{3}{4}{x^{ - \dfrac{7}{4}}} < 0,\forall x \in \left( {0, + \infty } \right)\) nên không đồng biến trên từng khoảng xác định, loại B.
Hàm số \(y = {x^4}\) có tập xác định là \(\mathbb{R}\) và có \(y' = 4{x^3}\) nên không đồng biến trên các khoảng xác định, loại C.
Hàm số \(y = \sqrt[3]{x}\) có tập xác định là \(\mathbb{R}\) và có \(y' = \dfrac{1}{{3\sqrt[3]{{{x^2}}}}} > 0\) nên hàm số đồng biến trên các khoảng xác định.
Hướng dẫn giải:
Tính đạo hàm của mỗi hàm số rồi xét dấu đạo hàm trên khoảng xác định \(D\).
Nếu \(y' \ge 0\) và bằng \(0\) tại hữu hạn điểm thuộc \(D\) thì hàm số đồng biến trên \(D\).
Hàm số \(y = {\left( {{x^2} - 4} \right)^{1 + \sqrt 5 }}\) có tập xác định là.
Điều kiện xác định của hàm số \(y = {\left( {{x^2} - 4} \right)^{1 + \sqrt 5 }}\) là: \({x^2} - 4 > 0 \Leftrightarrow \left[ \begin{array}{l}x < - 2\\x > 2\end{array} \right.\).
Suy ra tập xác định của hàm số là: \(D = \left( { - \infty ; - 2} \right) \cup \left( {2; + \infty } \right)\).
Hướng dẫn giải:
Hàm số \(y = {x^\alpha }\) với \(\alpha \) không nguyên thì xác định trên \(\left( {0; + \infty } \right)\).
Cho hàm số $y = x.{e^{ - x}}$. Chọn kết luận đúng:
Hàm số xác định và liên tục trên \(\mathbb{R}.\)
Ta có $y' = {e^{ - x}} + x.\left( { - {e^{ - x}}} \right) = {e^{ - x}}\left( {1 - x} \right)$$ \Rightarrow y' = 0 \Leftrightarrow 1 - x = 0 \Leftrightarrow x = 1$
Với \(x > 1\) thì \(y' < 0\) và với \(x < 1\) thì \(y' > 0\) nên \(y'\) đổi dấu từ dương sang âm qua điểm \(x = 1\).
Vậy hàm số đạt cực đại tại $x = 1$.
Hướng dẫn giải:
- Tính \(y'\) và giải phương trình \(y' = 0\).
- Xét dấu \(y'\) suy ra điểm cực trị của hàm số.
Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y = {\log _{2020}}\left( {mx - m + 2} \right)\) xác định trên \(\left[ {1; + \infty } \right).\)
ĐKXĐ: \(mx - m + 2 > 0 \Leftrightarrow m\left( {x - 1} \right) > - 2\)
Để hàm số xác định trên \(\left[ {1; + \infty } \right)\) thì \(m\left( {x - 1} \right) > - 2\,\,(*),\,\,\forall x \ge 1\)
+) \(x = 1 \Rightarrow \) (*) \( \Leftrightarrow 0m > - 2\) đúng với mọi m
+) \(x > 1 \Rightarrow \) (*) \( \Leftrightarrow m > \dfrac{{ - 2}}{{x - 1}}\), \(\forall x > 1\) (2*).
Xét hàm số \(f\left( x \right) = \dfrac{{ - 2}}{{x - 1}}\,\,\forall x > 1\)ta có \(f'\left( x \right) = \dfrac{2}{{{{\left( {x - 1} \right)}^2}}} > 0\,\,\forall x \in \left( {1; + \infty } \right)\).
BBT:
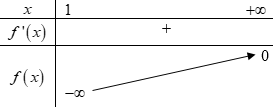
Dựa vào BBT \( \Rightarrow m \ge 0\).
Vậy để hàm số \(y = {\log _{2020}}\left( {mx - m + 2} \right)\) xác định trên \(\left[ {1; + \infty } \right)\) thì \(m \ge 0\).
Hướng dẫn giải:
TXĐ của hàm số \(y = {\log _a}x\,\,\left( {0 < a \ne 1} \right)\) là \(D = \left( {0; + \infty } \right)\).
Phương trình \({2^{{{\log }_5}\left( {x + 3} \right)}} = x\) có tất cả bao nhiêu nghiệm?
Điều kiện: \(x > - 3.\)
Do ${2^{{{\log }_5}\left( {x + 3} \right)}} > 0$ nên để phương trình có nghiệm thì \(x > 0.\)
Lấy logarit cơ số \(2\) của hai vế phương trình, ta được ${\log _5}\left( {x + 3} \right) = {\log _2}x$.
Đặt $t = {\log _5}\left( {x + 3} \right) = {\log _2}x$$ \Rightarrow \left\{ \begin{array}{l}x + 3 = {5^t}\\x = {2^t}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = {5^t} - 3\\x = {2^t}\end{array} \right.$ $ \Leftrightarrow {5^t} - 3 = {2^t} \Leftrightarrow {5^t} = {3.1^t} + {2^t}$
Chia hai vế phương trình cho ${5^t}$, ta được $1 = 3.{\left( {\dfrac{1}{5}} \right)^t} + {\left( {\dfrac{2}{5}} \right)^t}$.
Đây là phương trình hoành độ giao điểm của đường \(y = 1\) (hàm hằng) và đồ thị hàm số $y = 3.{\left( {\dfrac{1}{5}} \right)^t} + {\left( {\dfrac{2}{5}} \right)^t}$ (hàm số này nghịch biến vì nó là tổng của hai hàm số nghịch biến).
Do đó phương trình có nghiệm duy nhất. Nhận thấy \(t = 1\) thỏa mãn phương trình.
Với \(t = 1 \Rightarrow x = {2^t} = 2\left( {TM} \right).\)
Vậy phương trình có nghiệm duy nhất.
Hướng dẫn giải:
- Logarit cơ số \(2\) hai vế đưa về phương trình logarit.
- Đặt ẩn phụ đưa phương trình về phương trình mũ với ẩn mới.
- Giải phương trình mới bằng phương pháp xét hàm đặc trưng.
Đề thi liên quan
-
Đề kiểm tra 15 phút chương 2: Hàm số lũy thừa, mũ, logarit - Đề số 1
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 15 phút chương 2: Hàm số lũy thừa, mũ, logarit - Đề số 3
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 1 tiết chương 2: Hàm số lũy thừa, mũ và logarit - Đề số 1
-
25 câu hỏi
-
45 phút
-
-
Đề kiểm tra 1 tiết chương 2: Hàm số lũy thừa, mũ và logarit - Đề số 2
-
25 câu hỏi
-
45 phút
-
-
Đề kiểm tra 1 tiết chương 2: Hàm số lũy thừa, mũ và logarit - Đề số 3
-
25 câu hỏi
-
45 phút
-

