Hàm số \(y = {\left( {{x^2} - 4} \right)^{1 + \sqrt 5 }}\) có tập xác định là.
A.
\(D = \left( { - \infty ; - 2} \right) \cup \left( {2; + \infty } \right)\).
B.
\(D = \mathbb{R}\).
C.
\(D = \left( { - \infty ; - 2} \right] \cup \left[ {2; + \infty } \right)\).
D.
\(D = \left[ { - 2;2} \right]\).
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: a
Điều kiện xác định của hàm số \(y = {\left( {{x^2} - 4} \right)^{1 + \sqrt 5 }}\) là: \({x^2} - 4 > 0 \Leftrightarrow \left[ \begin{array}{l}x < - 2\\x > 2\end{array} \right.\).
Suy ra tập xác định của hàm số là: \(D = \left( { - \infty ; - 2} \right) \cup \left( {2; + \infty } \right)\).
Hướng dẫn giải:
Hàm số \(y = {x^\alpha }\) với \(\alpha \) không nguyên thì xác định trên \(\left( {0; + \infty } \right)\).
Điều kiện xác định của hàm số \(y = {\left( {{x^2} - 4} \right)^{1 + \sqrt 5 }}\) là: \({x^2} - 4 > 0 \Leftrightarrow \left[ \begin{array}{l}x < - 2\\x > 2\end{array} \right.\).
Suy ra tập xác định của hàm số là: \(D = \left( { - \infty ; - 2} \right) \cup \left( {2; + \infty } \right)\).
Hướng dẫn giải:
Hàm số \(y = {x^\alpha }\) với \(\alpha \) không nguyên thì xác định trên \(\left( {0; + \infty } \right)\).
CÂU HỎI CÙNG CHỦ ĐỀ
Xét hàm số \(y = {x^\alpha }\) trên tập \(\left( {0; + \infty } \right)\) có đồ thị dưới đây, chọn kết luận đúng:

Tìm tập nghiệm \(S\) của phương trình ${\log _6}\left[ {x\left( {5 - x} \right)} \right] = 1.$
Trong các hàm số sau đây, hàm số nào đồng biến trên các khoảng xác định?
Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y = {\log _{2020}}\left( {mx - m + 2} \right)\) xác định trên \(\left[ {1; + \infty } \right).\)
Phương trình \({2^{{{\log }_5}\left( {x + 3} \right)}} = x\) có tất cả bao nhiêu nghiệm?
Giải phương trình \({\log _3}\left( {x + 2} \right) + {\log _9}{\left( {x + 2} \right)^2} = \dfrac{5}{4}\)
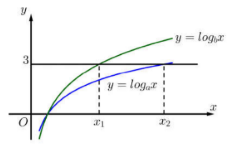
Hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) có đồ thị như hình vẽ bên:
Đường thẳng \(y = 3\) cắt hai đồ thị tại các điểm có hoành độ \({x_1},\,\,{x_2}.\) Biết rằng \({x_2} = 2{x_1},\) giá trị của \(\dfrac{a}{b}\) bằng:
Số nghiệm của phương trình \({2^{2{x^2} - 7x + 5}} = 1\) là:
Tổng các nghiệm của phương trình \({3^{{x^4} - 3{x^2}}} = 81\)

