Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: d
Hàm số \(y = {x^{ - 4}}\) có tập xác định là \(\mathbb{R}\backslash \left\{ 0 \right\}\) và có \(y' = - 4{x^{ - 5}}\) nên không đồng biến trên các khoảng xác định (đồng biến trên \(\left( { - \infty ,0} \right)\) và nghịch biến trên \(\left( {0, + \infty } \right)\)), loại A.
Hàm số \(y = {x^{ - \dfrac{3}{4}}}\) có tập xác định là \(\left( {0, + \infty } \right)\) và có \(y' = - \dfrac{3}{4}{x^{ - \dfrac{7}{4}}} < 0,\forall x \in \left( {0, + \infty } \right)\) nên không đồng biến trên từng khoảng xác định, loại B.
Hàm số \(y = {x^4}\) có tập xác định là \(\mathbb{R}\) và có \(y' = 4{x^3}\) nên không đồng biến trên các khoảng xác định, loại C.
Hàm số \(y = \sqrt[3]{x}\) có tập xác định là \(\mathbb{R}\) và có \(y' = \dfrac{1}{{3\sqrt[3]{{{x^2}}}}} > 0\) nên hàm số đồng biến trên các khoảng xác định.
Hướng dẫn giải:
Tính đạo hàm của mỗi hàm số rồi xét dấu đạo hàm trên khoảng xác định \(D\).
Nếu \(y' \ge 0\) và bằng \(0\) tại hữu hạn điểm thuộc \(D\) thì hàm số đồng biến trên \(D\).
Hàm số \(y = {x^{ - 4}}\) có tập xác định là \(\mathbb{R}\backslash \left\{ 0 \right\}\) và có \(y' = - 4{x^{ - 5}}\) nên không đồng biến trên các khoảng xác định (đồng biến trên \(\left( { - \infty ,0} \right)\) và nghịch biến trên \(\left( {0, + \infty } \right)\)), loại A.
Hàm số \(y = {x^{ - \dfrac{3}{4}}}\) có tập xác định là \(\left( {0, + \infty } \right)\) và có \(y' = - \dfrac{3}{4}{x^{ - \dfrac{7}{4}}} < 0,\forall x \in \left( {0, + \infty } \right)\) nên không đồng biến trên từng khoảng xác định, loại B.
Hàm số \(y = {x^4}\) có tập xác định là \(\mathbb{R}\) và có \(y' = 4{x^3}\) nên không đồng biến trên các khoảng xác định, loại C.
Hàm số \(y = \sqrt[3]{x}\) có tập xác định là \(\mathbb{R}\) và có \(y' = \dfrac{1}{{3\sqrt[3]{{{x^2}}}}} > 0\) nên hàm số đồng biến trên các khoảng xác định.
Hướng dẫn giải:
Tính đạo hàm của mỗi hàm số rồi xét dấu đạo hàm trên khoảng xác định \(D\).
Nếu \(y' \ge 0\) và bằng \(0\) tại hữu hạn điểm thuộc \(D\) thì hàm số đồng biến trên \(D\).
CÂU HỎI CÙNG CHỦ ĐỀ
Xét hàm số \(y = {x^\alpha }\) trên tập \(\left( {0; + \infty } \right)\) có đồ thị dưới đây, chọn kết luận đúng:

Hàm số \(y = {\left( {{x^2} - 4} \right)^{1 + \sqrt 5 }}\) có tập xác định là.
Tìm tập nghiệm \(S\) của phương trình ${\log _6}\left[ {x\left( {5 - x} \right)} \right] = 1.$
Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y = {\log _{2020}}\left( {mx - m + 2} \right)\) xác định trên \(\left[ {1; + \infty } \right).\)
Phương trình \({2^{{{\log }_5}\left( {x + 3} \right)}} = x\) có tất cả bao nhiêu nghiệm?
Giải phương trình \({\log _3}\left( {x + 2} \right) + {\log _9}{\left( {x + 2} \right)^2} = \dfrac{5}{4}\)
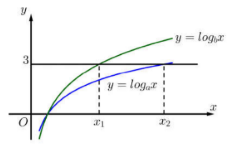
Hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) có đồ thị như hình vẽ bên:
Đường thẳng \(y = 3\) cắt hai đồ thị tại các điểm có hoành độ \({x_1},\,\,{x_2}.\) Biết rằng \({x_2} = 2{x_1},\) giá trị của \(\dfrac{a}{b}\) bằng:
Số nghiệm của phương trình \({2^{2{x^2} - 7x + 5}} = 1\) là:
Tổng các nghiệm của phương trình \({3^{{x^4} - 3{x^2}}} = 81\)

