Đề kiểm tra 1 tiết chương 5: Khối đa diện và thể tích - Đề số 3
-
Hocon247
-
25 câu hỏi
-
45 phút
-
657 lượt thi
-
Dễ
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Phép dời hình biến mặt phẳng thành:
Phép dời hình biến mặt phẳng thành mặt phẳng.
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác cân tại $A$. \(AB = AC = 2a,\widehat {CAB} = {120^0}.\) Mặt phẳng \(\left( {AB'C'} \right)\) tạo với đáy một góc \({60^0}\). Thể tích khối lăng trụ là:
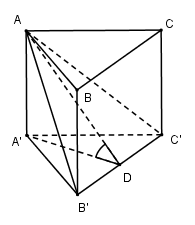
Gọi $D$ là trung điểm của $B'C'$. Vì tam giác \(A'B'C'\) cân tại $A'$ nên \(A'D \bot B'C'\) (trung tuyến đồng thời là đường cao).
Vì $ABC.A'B'C'$ là hình lăng trụ đứng nên $AA' \bot (A'B'C')$.
Ta có: \(\left. \begin{array}{l}A'D \bot B'C'\\AA' \bot B'C'\end{array} \right\} \Rightarrow B'C' \bot \left( {AA'D} \right) \Rightarrow B'C' \bot AD\)
\(\left. \begin{array}{l}\left( {AB'C'} \right) \cap \left( {A'B'C'} \right) = B'C'\\\left( {AB'C'} \right) \supset AD \bot B'C'\\\left( {A'B'C'} \right) \supset A'D \bot B'C'\end{array} \right\} \Rightarrow \widehat {\left( {\left( {AB'C'} \right);\left( {A'B'C'} \right)} \right)} = \widehat {\left( {AD;A'D} \right)} = \widehat {ADA'} = {60^0}\)
Vì tam giác \(A'B'C'\) cân tại $A'$ nên \(\widehat {DA'C'} = \dfrac{1}{2}\widehat {B'A'C'} = {60^0}\) (trung tuyến đồng thời là phân giác)
Xét tam giác vuông \(A'D'C'\) có: \(A'D = A'C'.cos60 = 2a.\dfrac{1}{2} = a\)
Xét tam giác vuông \(AA'D\) có: \(AA' = A'D.\tan 60 = a.\sqrt 3 \)
\({S_{ABC}} = \dfrac{1}{2}AB.AC.\sin \widehat {BAC} = \dfrac{1}{2}.2a.2a.\dfrac{{\sqrt 3 }}{2} = {a^2}\sqrt 3 \)
Vậy \({V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = a\sqrt 3 .{a^2}\sqrt 3 = 3{a^3}\)
Hướng dẫn giải:
- Xác định góc giữa hai mặt phẳng \(\left( {AB'C'} \right)\) và \(\left( {A'B'C'} \right)\): góc giữa hai mặt phẳng là góc giữa hai đường thẳng nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến.
- Tính độ dài đường cao \(h = AA'\).
- Tính diện tích đáy \({S_{A'B'C'}}\).
- Tính thể tích khối lăng trụ \(V = Sh\).
Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \({V_1};{V_2}\) lần lượt là thể tích của khối tứ diện \(ACB'D'\) và khối hộp \(ABCD.A'B'C'D'.\) Tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\) bằng
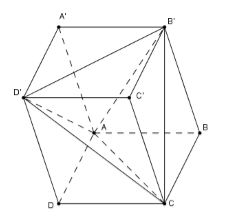
Ta thấy \({V_1} = {V_{ABCD.A'B'C'D'}} = h.{S_{ABCD}}\) với \(h = d\left( {A',\left( {ABCD} \right)} \right)\)
+) \({V_{D'.ADC}} = \dfrac{1}{3}d\left( {D',\left( {ADC} \right)} \right).{S_{\Delta ADC}} = \dfrac{1}{3}.h.\dfrac{1}{2}{S_{ABCD}} = \dfrac{1}{6}{V_1}\)
Tương tự ta có \({V_{C.D'C'B'}} = {V_{B'.ABC}} = {V_{A.A'B'D'}} = {V_{D'.ADC}} = \dfrac{1}{6}{V_1}\)
Lại có \({V_{C.D'C'B'}} + {V_{B'.ABC}} + {V_{A.A'B'D'}} + {V_{D'.ADC}} + {V_{ACB'D'}} = {V_{ABCD.A'B'C'D'}}\)
\( \Leftrightarrow {V_2} = {V_{ACB'D'}} = {V_1} - 4.\dfrac{1}{6}{V_1} = \dfrac{{{V_1}}}{3} \Leftrightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{1}{3}\).
Hướng dẫn giải:
Thể tích khối chóp \(V = \dfrac{1}{3}S.h\).
Thể tích khối hộp \(V = S.h\).
Khối đa diện lồi có \(8\) đỉnh và \(6\) mặt thì có số cạnh là:
Ta có: \(D = 8,M = 6\) thì \(D - C + M = 2 \Leftrightarrow 8 - C + 6 = 2 \Leftrightarrow C = 12\)
Vậy số cạnh là \(12\).
Hướng dẫn giải:
Sử dụng định lý Ơ le cho khối đa diện lồi \(D - C + M = 2\)
Cho khối đa diện lồi có số đỉnh, số mặt và số cạnh lần lượt là \(D,M,C\). Chọn mệnh đề đúng:
Khối đa diện lồi có \(D\) đỉnh, \(M\) mặt và \(N\) cạnh thì \(D - C + M = 2\).
Giải thích thêm:
Một số em sẽ chọn sai đáp án B hặc D vì nhớ nhầm công thức.
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(A,\,\,AB = a,\) cạnh bên \(SC = 3a\) và \(SC\) vuông góc với mặt phẳng đáy. Thể tích khối chóp \(S.ABC\) bằng:
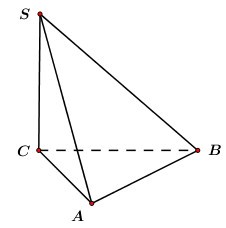
Ta có:\({S_{ABC}} = \dfrac{1}{2}A{B^2} = \dfrac{1}{2}{a^2}.\)
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SC.{S_{ABC}} = \dfrac{1}{3}.3a.\dfrac{1}{2}{a^2} \)\(= \dfrac{1}{2}{a^3}.\)
Hướng dẫn giải:
Thể tích khối chóp có chiều cao \(h\) và diện tích đáy \(S\) là \(V = \frac{1}{3}Sh.\)
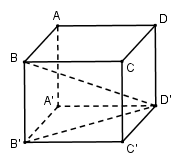
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Hình nào dưới đây bằng hình lăng trụ \(ABC.A'B'C'\)?
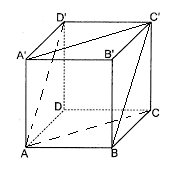
Ta thấy hai lăng trụ đứng \(ABC.A'B'C'\) và \(AA'D'.BB'C'\) có một phép đối xứng qua mặt phẳng \(\left( {AB'C'D} \right)\) nên hai lăng trụ này bằng nhau.
Cho hình lăng trụ \(ABC.A'B'C'\) có \(AB = 2a,AC = a,AA' = \dfrac{{a\sqrt {10} }}{2},\widehat {BAC} = {120^0}\). Hình chiếu vuông góc của $C’$ lên $(ABC)$ là trung điểm của cạnh $BC$. Tính thể tích khối lăng trụ \(ABC.A'B'C'\) theo $a$?
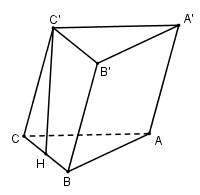
Áp dụng định lí Côsin trong tam giác $ABC$ có: \(BC = \sqrt {A{B^2} + A{C^2} - 2AB.AC.\cos 120} \)
$= \sqrt {4{a^2} + {a^2} - 2.2a.a.\dfrac{{ - 1}}{2}} = a\sqrt 7 \Rightarrow CH = \dfrac{1}{2}BC = \dfrac{{a\sqrt 7 }}{2}$
\(C'H \bot \left( {ABC} \right) \Rightarrow C'H \bot CH \Rightarrow \Delta CC'H\) vuông tại $H$
\( \Rightarrow C'H = \sqrt {CC{'^2} - C{H^2}} = \sqrt {\dfrac{{10{a^2}}}{4} - \dfrac{{7{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{2}\)
\({S_{ABC}} = \dfrac{1}{2}AB.AC.\sin 120 = \dfrac{1}{2}.2a.a.\dfrac{{\sqrt 3 }}{2} = \dfrac{{{a^2}\sqrt 3 }}{2}\)
Vậy \({V_{ABC.A'B'C'}} = C'H.{S_{ABC}} = \dfrac{{a\sqrt 3 }}{2}.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{3{a^3}}}{4}\)
Hướng dẫn giải:
- Tính diện tích đáy \({S_{ABC}}\).
- Tính độ dài đường cao.
- Tính thể tích khối lăng trụ theo công thức \(V = Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao.
Cho lăng trụ xiên tam giác $ABC.A'B'C'$ có đáy $ABC$ là tam giác đều cạnh $a$, biết cạnh bên là \(a\sqrt 3 \) và hợp với đáy $ABC$ một góc \({60^0}\). Thể tích khối lăng trụ là:
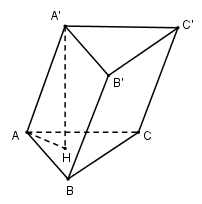
Gọi $H$ là hình chiếu vuông góc của $A'$ trên \(\left( {ABC} \right) \Rightarrow A'H \bot \left( {ABC} \right)\)
\( \Rightarrow AH\) là hình chiếu vuông góc của $AA'$ trên \(\left( {ABC} \right) \Rightarrow \widehat {\left( {AA';\left( {ABC} \right)} \right)} = \widehat {\left( {AA';AH} \right)} = \widehat {A'AH} = {60^0}\)
\(A'H \bot \left( {ABC} \right) \Rightarrow A'H \bot AH \Rightarrow \Delta A'AH\) vuông tại \(H \Rightarrow A'H = AA'.\sin 60 = a\sqrt 3 .\dfrac{{\sqrt 3 }}{2} = \dfrac{{3a}}{2}\)
Tam giác $ABC$ đều cạnh nên \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Vậy \({V_{ABC.A'B'C'}} = A'H.{S_{ABC}} = \dfrac{{3a}}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{3{a^3}\sqrt 3 }}{8}\)
Hướng dẫn giải:
- Tính diện tích đáy \({S_{\Delta ABC}}\)
- Xác định góc \({60^0}\): góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
- Tính độ dài đường cao của lăng trụ.
- Tính thể tích lăng trụ theo công thức \(V = Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao.
Cho hình chóp \(S.\,ABC\) có \(SA\) vuông góc với đáy. Tam giác \(ABC\) vuông cân tại \(B\), biết \(SA = AC = 2a\). Thể tích khối chóp \(S.ABC\) là
Do \(\Delta ABC\) vuông cân tại \(B\) có \(AC = 2a \Rightarrow AB = BC = \dfrac{{AC}}{{\sqrt 2 }} = a\sqrt 2 \).
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SA.\dfrac{1}{2}BA.BC = \dfrac{1}{6}.2a.a\sqrt 2 .a\sqrt 2 = \dfrac{{2{a^3}}}{3}\).
Hướng dẫn giải:
Sử dụng công thức tính thể tích khối chóp \(V = \dfrac{1}{3}{S_{day}}.h\).
Trong một hình đa diện lồi, mỗi cạnh là cạnh chung của tất cả bao nhiêu mặt?
Hình đa diện lồi cũng là hình đa diện nên mỗi cạnh của nó là cạnh chung của đúng \(2\) mặt.
Giải thích thêm:
Một số em sẽ chọn đáp án D vì nhớ nhầm định nghĩa hình đa diện.
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy là tứ giác đều cạnh $a$, biết rằng \(BD' = a\sqrt 6 \) . Tính thể tích của khối lăng trụ?
Vì $A'B'C'D'$ là hình vuông cạnh $a$ nên \(B'D' = a\sqrt 2 \)
\(BB' \bot \left( {A'B'C'D'} \right) \Rightarrow BB' \bot B'D' \Rightarrow \Delta BB'D'\) vuông tại \(B' \Rightarrow BB' = \sqrt {BD{'^2} - B'D{'^2}} = \sqrt {6{a^2} - 2{a^2}} = 2a\)
Vậy \({V_{ABCD.A'B'C'D'}} = BB'.{S_{ABCD}} = 2a.{a^2} = 2{a^3}\)
Hướng dẫn giải:
- Tính diện tích đáy \({S_{A'B'C'D'}}\) và độ dài đường cao \(BB'\).
- Tính thể tích khối lăng trụ theo công thức \(V = Sh\).
Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $a$ và mặt bên hợp với đáy một góc \({60^0}\). Thể tích khối chóp $S.ABC$ là:
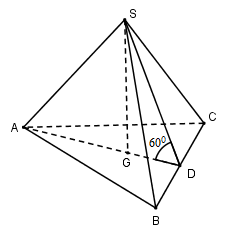
Bước 1:
Gọi $G$ là trọng tâm tam giác $ABC$. Vì chóp $S.ABC$ đều nên \(SG \bot \left( {ABC} \right)\)
Gọi $D$ là trung điểm của $BC$ ta có: \(AD \bot BC\)
Ta có: \(\left. \begin{array}{l}BC \bot AD\\BC \bot SG\,\,\left( {SG \bot \left( {ABC} \right)} \right)\end{array} \right\} \Rightarrow BC \bot \left( {SAD} \right) \Rightarrow BC \bot SD\)
\(\left. \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SD \bot BC\\\left( {ABC} \right) \supset AD \bot BC\end{array} \right\} \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SD;AD} \right)} = \widehat {SDA} = {60^0}\)
Bước 2:
Vì tam giác $ABC$ đều cạnh $a$ nên \(AD = \dfrac{{a\sqrt 3 }}{2} \Rightarrow DG = \dfrac{1}{3}AD = \dfrac{{a\sqrt 3 }}{6}\)
\(SG \bot \left( {ABC} \right) \Rightarrow SG \bot AD \Rightarrow \Delta SGD\) vuông tại $G$
\( \Rightarrow SG = GD.\tan 60 = \dfrac{{a\sqrt 3 }}{6}.\sqrt 3 = \dfrac{a}{2}\)
Bước 3:
Tam giác $ABC$ đều \( \Rightarrow {S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Bước 4:
\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SG.{S_{\Delta ABC}} = \dfrac{1}{3}.\dfrac{a}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{24}}\).
Hướng dẫn giải:
Bước 1: Xác định góc giữa mặt bên và mặt đáy: là góc giữa hai đường thẳng nằm trong hai mặt phẳng đó và cùng vuông góc với giao tuyến.
Bước 2: Tính chiều cao \(SG\)
Bước 3: Tính diện tích đáy \({S_{ABC}}\).
Bước 4: Tính thể tích theo công thức \(V = \dfrac{1}{3}Sh\).
Trong các mệnh đề sau, mệnh đề nào đúng?
Hình đa diện luôn có số đỉnh và số mặt nhỏ hơn số cạnh
Không phải hình đa diện nào cũng có số đỉnh bằng số mặt, ví dụ hình lập phương có 8 đỉnh và 6 mặt
Hình tứ diện có số đỉnh bằng số mặt (bằng 4).
Hướng dẫn giải:
Sử dụng định nghĩa hình đa diện và lấy ví dụ cho những hình đa diện quen thuộc.
Giải thích thêm:
Một số em sẽ chọn đáp án C khi lấy ví dụ tứ diện mà không chú ý đến trường hợp hình hộp.
Có tất cả bao nhiêu loại khối đa diện đều?
Chỉ có $5$ loại khối đa diện đều là tứ diện đều, khối lập phương, khối bát diện đều, khối $12$ mặt đều và khối $20$ mặt đều.
Giải thích thêm:
Một số em có thể sẽ chọn nhầm đáp án C vì nghĩ giống như đối với các hình đa giác đều trong mặt phẳng (có vô số đa giác đều trong mặt phẳng).
Cho bốn hình sau đây. Mệnh đề nào sau đây sai:
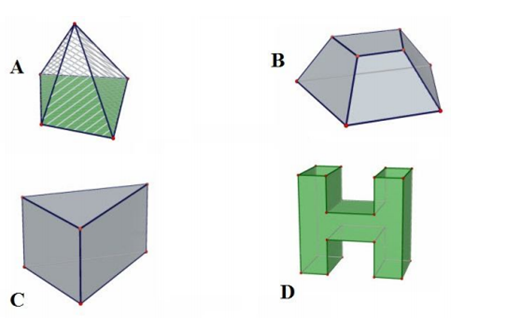
Khối đa diện A là khối chóp tứ giác.
Khối đa diện D không phải là khối đa diện lồi
Khối đa diện B, C là khối đa diện lồi
Mệnh đề nào sau đây là mệnh đề đúng?
Đa diện đều có tất cả các mặt là các đa giác bằng nhau.
Không tồn tại đa diện đều có $5$ và $6$ đỉnh, do đó chóp $S.ABCD$ và lăng trụ $ABC.A'B'C'$ không thể là đa diện đều.
Nếu mỗi đỉnh là đỉnh chung của đúng $3$ mặt thì nó cũng là đỉnh chung của đúng $3$ cạnh. Giả sử số đỉnh của đa diện là $n$ thì số cạnh của nó phải là $\dfrac{{3n}}{2}$ (vì mỗi cạnh được tính $2$ lần), do đó $n$ chẵn.
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\). Biết \(AC = a\sqrt 2 \), cạnh \(SC\) tạo với đáy một góc \({60^0}\) và diện tích tứ giác \(ABCD\) là \(\dfrac{{3{a^2}}}{2}\). Gọi \(H\) là hình chiếu của \(A\) trên cạnh \(SC\). Tính thể tích khối chóp \(H.ABCD\).
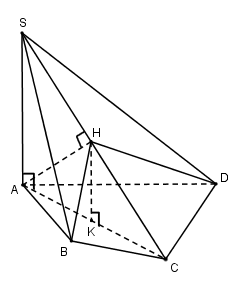
Ta có: \(SA \bot \left( {ABCD} \right) \Rightarrow AC\)là hình chiếu của $SC$ trên \(\left( {ABCD} \right) \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {\left( {SC;AC} \right)} = {60^0}\)
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow \Delta SAC\) vuông tại $A$ và $\widehat {SCA} = {60^0}$
Xét tam giác vuông $SAC$ có: \(SA = AC.\tan 60 = a\sqrt 2 .\sqrt 3 = a\sqrt 6 ;\,SC = \dfrac{{AC}}{{{\rm{cos60}}}} = \dfrac{{a\sqrt 2 }}{{\dfrac{1}{2}}} = 2a\sqrt 2 \)
Áp dụng hệ thức lượng trong tam giác vuông $SAC$ có: \(A{C^2} = HC.SC \Rightarrow \dfrac{{HC}}{{SC}} = \dfrac{{A{C^2}}}{{S{C^2}}} = \dfrac{{2{a^2}}}{{8{a^2}}} = \dfrac{1}{4}\)
Trong $\left( {SAC} \right)$ kẻ \(HK//SA \Rightarrow HK \bot \left( {ABCD} \right)\)
Ta có: \(\dfrac{{HK}}{{SA}} = \dfrac{{HC}}{{SC}} = \dfrac{1}{4} \Rightarrow HK = \dfrac{1}{4}SA = \dfrac{{a\sqrt 6 }}{4}\)
Vậy \({V_{H.ABCD}} = \dfrac{1}{3}HK.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{a\sqrt 6 }}{4}.\dfrac{{3{a^2}}}{2} = \dfrac{{{a^3}\sqrt 6 }}{8}\)
Hướng dẫn giải:
- Xác định góc giữa \(SC\) và mặt phẳng đáy: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
- Dựng đường cao \(HK\) của hình chóp \(H.ABCD\) và tính độ dài \(HK\) dựa vào định lý Ta-let.
- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\).
Khối chóp tam giác có độ dài 3 cạnh xuất phát từ một đỉnh là \(a,\,\,2a,\,\,3a\) có thể tích lớn nhất bằng
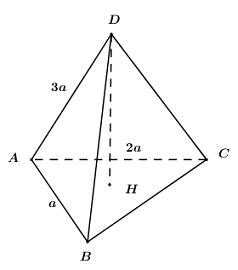
Giả sử khối chóp \(ABCD\) có \(AB = a,\,\,AC = 2a,\,\,AD = 3a\).
Gọi \(H\) là hình chiếu vuông góc của \(D\) lên \(\left( {ABC} \right)\), khi đó ta có: \(DH \bot \left( {ABC} \right)\) và \(DH \le AD\).
Ta có: \({S_{ABC}} = \dfrac{1}{2}AB.AC.\sin \angle BAC \le \dfrac{1}{2}AB.AC\).
Vây \({V_{ABCD}} = \dfrac{1}{3}DH.{S_{\Delta ABC}} \le \dfrac{1}{3}AD.\dfrac{1}{2}AB.AC = \dfrac{1}{6}AB.AC.AD = \dfrac{1}{6}.a.2a.3a = {a^3}\).
Dấu “=” xảy ra \( \Leftrightarrow AD \bot \left( {ABC} \right),\,\,AB \bot AC\) hay \(AB,\,\,AC,\,\,AD\) đôi một vuông góc.
Hướng dẫn giải:
Khối chóp có thể tích lớn nhất khi 3 cạnh đôi một vuông góc.
Cho lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác đều cạnh $a$, và \(A'A = A'B = A'C = a\sqrt {\dfrac{7}{{12}}} \) . Thể tích khối lăng trụ \(ABC.A'B'C'\) theo $a$ là:
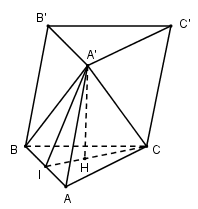
Gọi $H$ là tâm tam giác đều $ABC$ . Vì $A'A = A'B = A'C$ nên hình chóp $A'.ABC$ là đều nên \(A'H \bot \left( {ABC} \right)\)
Gọi $I$ là trung điểm của $AB$.
Vì tam giác $ABC$ đều cạnh $a$ nên \(CI = \dfrac{{a\sqrt 3 }}{2} \Rightarrow HI = \dfrac{1}{3}CI = \dfrac{{a\sqrt 3 }}{6}\)
Tam giác $A'AB$ cân tại $A'$ nên \(A'I \bot AB \Rightarrow \Delta A'AI\) vuông tại \(I \Rightarrow A'I = \sqrt {AA{'^2} - A{I^2}} = \sqrt {\dfrac{{7{a^2}}}{{12}} - \dfrac{{{a^2}}}{4}} = \dfrac{a}{{\sqrt 3 }}\)
\(A'H \bot \left( {ABC} \right) \Rightarrow A'H \bot HI \Rightarrow \Delta A'HI\) vuông tại \(H \Rightarrow A'H = \sqrt {A'{I^2} - H{I^2}} = \sqrt {\dfrac{{{a^2}}}{3} - \dfrac{{{a^2}}}{{12}}} = \dfrac{a}{2}\)
Vì tam giác $ABC$ đều cạnh $a$ nên \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Vậy \({V_{ABC.A'B'C'}} = A'H.{S_{ABC}} = \dfrac{a}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{8}\)
Hướng dẫn giải:
- Tính diện tích đáy \({S_{ABC}}\).
- Xác định chiều cao của khối lăng trụ dựa vào tính chất của hình chóp đều.
- Tính thể tích khối lăng trụ theo công thức \(V = Sh\) với \(S\) là diện tích đáy và \(h\) là chiều cao.
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\)có \(AB = a,\) đường thẳng \(A'B\) tạo với mặt phẳng \(\left( {BCC'B'} \right)\) một góc \({30^0}.\) Tính thể tích khối lăng trụ \(ABC.A'B'C'.\)
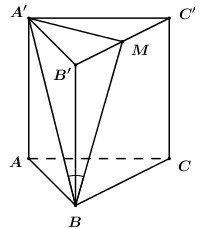
Gọi \(M\) là trung điểm của \(B'C'\). Vì \(\Delta A'B'C'\) đều nên \(A'M \bot B'C'\).
Ta có: \(\left\{ \begin{array}{l}A'M \bot B'C'\\A'M \bot BB'\,\,\left( {BB' \bot \left( {A'B'C'} \right)} \right)\end{array} \right.\) \( \Rightarrow A'M \bot \left( {BCC'B'} \right)\).
\( \Rightarrow BM\) là hình chiếu của \(A'M\) lên \(\left( {BCC'B'} \right)\) \( \Rightarrow \angle \left( {A'B;\left( {BCC'B'} \right)} \right) = \angle \left( {A'B;MB} \right) = \angle A'BM = {30^0}\).
Theo bài ra ta có \(\Delta A'B'C'\) đều cạnh \(a\) nên \(A'M = \dfrac{{a\sqrt 3 }}{2}\) và \({S_{\Delta A'B'C'}} = \dfrac{{{a^2}\sqrt 3 }}{4}\).
Ta có: \(A'M \bot \left( {BCC'B'} \right) \Rightarrow A'M \bot BM\) \( \Rightarrow \Delta A'BM\) vuông tại \(M\) \( \Rightarrow BM = A'M.\cot {30^0} = \dfrac{{3a}}{2}\).
Áp dụng định lí Pytago trong tam giác vuông \(BB'M\) ta có: \(BB' = \sqrt {B{M^2} - BB{'^2}} = \sqrt {{{\left( {\dfrac{{3a}}{2}} \right)}^2} - {{\left( {\dfrac{a}{2}} \right)}^2}} = a\sqrt 2 \).
Vậy \({V_{ABC.A'B'C'}} = BB'.{S_{A'B'C'}} = a\sqrt 2 .\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 6 }}{4}\).
Hướng dẫn giải:
- Xác định góc giữa \(A'B\) và \(\left( {BCC'B'} \right)\) là góc giữa \(A'B\) và hình chiếu của \(A'B\) lên \(\left( {BCC'B'} \right)\).
- Sử dụng công thức tính nhanh: Chiều cao của tam giác đều cạnh \(a\) là \(\dfrac{{a\sqrt 3 }}{2}\) và diện tích tam giác đều cạnh \(a\) là \(\dfrac{{{a^2}\sqrt 3 }}{4}\).
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông và định lí Pytago để tính chiều cao của khối lăng trụ.
- Sử dụng công thức tính thể tích khối lăng trụ có chiều cao \(h\), diện tích đáy \(B\) là \(V = B.h\).
Cho hình chóp \(S.ABC\), đáy là tam giác \(ABC\) có \(AB = BC\sqrt 5 \), \(AC = 2BC\sqrt 2 \), hình chiếu của \(S\) lên mặt phẳng \(\left( {ABC} \right)\) là trung điểm \(O\) của cạnh \(AC\). Khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng 2. Mặt phẳng \(\left( {SBC} \right)\) hợp với mặt phẳng \(\left( {ABC} \right)\) một góc \(\alpha \) thay đổi. Biết rằng giá trị nhỏ nhất của thể tích khối chóp \(S.ABC\) bằng \(\dfrac{{\sqrt a }}{b}\), trong đó \(a,\,\,b \in {\mathbb{N}^*}\), \(a\) là số nguyên tố. Tổng \(a + b\) bằng:
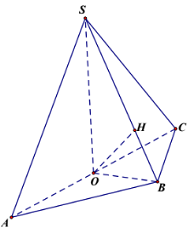
Gọi \(H\) là hình chiếu của \(O\) lên \(SB\).
Ta có: \(OB = \sqrt {\dfrac{{2B{C^2} + 2B{A^2} - A{C^2}}}{4}} = BC\), \(OC = \dfrac{1}{2}AC = BC\sqrt 2 \). Suy ra \(OB \bot BC\).
Dễ thấy \(\angle SBO = \alpha \) và \(OH = d\left( {O;\left( {SBC} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {SBC} \right)} \right) = 1\).
Suy ra \(SO = \dfrac{{OH}}{{\cos \alpha }} = \dfrac{1}{{\cos \alpha }}\), \(OB = \dfrac{{OH}}{{\sin \alpha }} = \dfrac{1}{{\sin \alpha }}\).
\( \Rightarrow BC = OB = \dfrac{1}{{\sin \alpha }}\).
Thể tích khối chóp \(S.ABC\) là:
\(\begin{array}{l}{V_{S.ABC}} = \dfrac{1}{3}SO.{S_{ABC}} = \dfrac{1}{3}SO.2{S_{OBC}}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}.\dfrac{1}{{\cos \alpha }}.{\left( {\dfrac{1}{{\sin \alpha }}} \right)^2} = \dfrac{1}{{3\cos \alpha .{{\sin }^2}\alpha }}\end{array}\)
Áp dụng bất đẳng thức Cô-si ta có:
\(\begin{array}{l}1 = \dfrac{1}{2}{\sin ^2}\alpha + \dfrac{1}{2}{\sin ^2}\alpha + {\cos ^2}\alpha \ge 3.\sqrt[3]{{\dfrac{1}{4}{{\sin }^4}\alpha .{{\cos }^2}\alpha }}\\ \Leftrightarrow \dfrac{1}{{27}} \ge \dfrac{1}{4}.si{n^4}\alpha .co{s^2}\alpha \Rightarrow \dfrac{1}{{{{\sin }^2}\alpha {{\cos }^2}\alpha }} \ge \dfrac{{3\sqrt 3 }}{2}\\ \Rightarrow {V_{S.ABC}} \ge \dfrac{{\sqrt 3 }}{2}\end{array}\)
Vậy \(\min {V_{S.ABC}} = \dfrac{{\sqrt 3 }}{2}\). Dấu “=” xảy ra \( \Leftrightarrow {\cos ^2}\alpha = \dfrac{1}{2}{\sin ^2}\alpha = \dfrac{1}{3} \Leftrightarrow \cos \alpha = \dfrac{{\sqrt 3 }}{3}\).
\( \Rightarrow a = 3,\,\,b = 2\).
Vậy \(a + b = 3 + 2 = 5\).
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\), \(SA\) vuông góc với mặt phẳng đáy \(\left( {ABCD} \right)\) và \(SA = a\). Điểm $M$ thuộc cạnh $SA$ sao cho \(\dfrac{{SM}}{{SA}} = k\). Xác định $k$ sao cho mặt phẳng \(\left( {BMC} \right)\) chia khối chóp \(S.ABCD\) thành hai phần có thể tích bằng nhau.
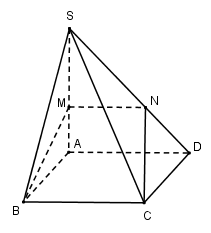
Vì $BC//AD$ nên mặt phẳng $\left( {BMC} \right)$ cắt $\left( {SAD} \right)$ theo đoạn thẳng $MN//AD\left( {N \in SD} \right)$
Vì \(MN//AD \Rightarrow \dfrac{{SM}}{{SA}} = \dfrac{{SN}}{{SD}} = k\)
$\begin{array}{l}\dfrac{{{V_{S.MBC}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SA}} = k \Rightarrow {V_{S.MBC}} = k.{V_{S.ABC}} = \dfrac{k}{2}.{V_{S.ABCD}}\\\dfrac{{{V_{S.MNC}}}}{{{V_{S.ADC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SN}}{{SD}} = {k^2} \Rightarrow {V_{S.MNC}} = {k^2}.{V_{S.ADC}} = \dfrac{{{k^2}}}{2}.{V_{S.ABCD}}\\ \Rightarrow {V_{S.MBCN}} = {V_{S.MBC}} + {V_{S.MNC}} = \left( {\dfrac{k}{2} + \dfrac{{{k^2}}}{2}} \right){V_{S.ABCD}}\end{array}$
Để mặt phẳng $\left( {BMNC} \right)$ chia hình chóp thành 2 phần có thể tích bằng nhau thì $\dfrac{k}{2} + \dfrac{{{k^2}}}{2} = \dfrac{1}{2} \Leftrightarrow {k^2} + k - 1 = 0 \Leftrightarrow k = \dfrac{{ - 1 + \sqrt 5 }}{2}$ do $k > 0$.
Hướng dẫn giải:
- Xác định thiết diện của hình chóp cắt bởi mặt phẳng \(\left( {BMC} \right)\).
- Chia khối chóp \(S.BCNM\) thành hai phần \(S.BCM\) và \(S.CNM\) và tính tỉ lệ thể tích của hai khối chóp đó với các khối chóp \(S.ABC\) và \(S.ACD\).
- Tính tỉ lệ thể tích của khối chóp \(S.BCNM\) với khối chóp \(S.ABCD\), từ đó dựa vào điều kiện đề bài tìm \(k\).
Đề thi THPT QG - 2021 - mã 101
Cho khối hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy là hình vuông, \(BD = 2a,\) góc giữa hai mặt phẳng \(\left( {A'B{\rm{D}}} \right)\) và \(\left( {ABCD} \right)\) bằng \({30^0}\). Thể tích của khối hộp chữ nhật đã cho bằng
* Xác định \(\angle \left( {\left( {A'BD} \right);\left( {ABCD} \right)} \right)\).
+ \(\left( {A'BC} \right) \cap \left( {ABCD} \right) = BD\).
+ \(\left\{ \begin{array}{l}AA' \bot BD\\AO \bot BD\end{array} \right. \Rightarrow \left( {A'AO} \right) \bot BD\).
+ \(\left\{ \begin{array}{l}\left( {A'AO} \right) \cap \left( {A'BD} \right) = A'O\\\left( {A'AO} \right) \cap \left( {ABCD} \right) = AO\end{array} \right.\)
\( \Rightarrow \angle \left( {\left( {A'BD} \right);\left( {ABCD} \right)} \right) = \angle \left( {A'O;AO} \right) = \angle A'OA\).
\( \Rightarrow \angle A'OA = {30^0}\).
* Xét tam giác \(A'OA\) vuông tại \(A\) có \(AO = \dfrac{1}{2}AC = \dfrac{1}{2}BD = a\).
\( \Rightarrow AA' = \tan {30^0}.AO = \dfrac{{a\sqrt 3 }}{3}\).
\( \Rightarrow {V_{ABCD.A'B'C'D'}} = {S_{ABCD}}.AA' = \dfrac{1}{2}AC.BD.AA'\) \( = \dfrac{1}{2}.{\left( {2a} \right)^2}.\dfrac{{a\sqrt 3 }}{3} = \dfrac{{2\sqrt 3 {a^3}}}{3}\).
Hướng dẫn giải:
- Xác định góc giữa hai mặt phẳng là góc tạo bởi 2 đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
- Sử dụng tính chất hình vuông và tỉ số lượng giác trong tam giác vuông để tính chiều cao \(AA'\).
- Tính thể tích khối lăng trụ.
Cho hình lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(A.\) Cạnh \(BC = 2a\) và \(\angle ABC = {60^0}.\) Biết tứ giác \(BCC'B'\) là hình thoi có \(\angle B'BC\) nhọn. Mặt phẳng \(\left( {BCC'B'} \right)\) vuông góc với \(\left( {ABC} \right)\) và mặt phẳng \(\left( {ABB'A'} \right)\) tạo với \(\left( {ABC} \right)\) góc \({45^0}.\) Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng:
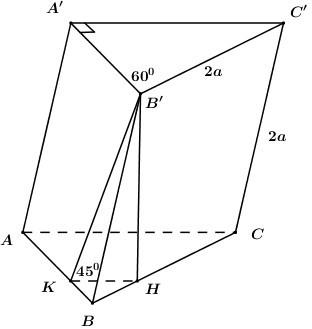
Trong \(\left( {BCC'B'} \right)\) kẻ \(B'H \bot BC\,\,\left( {H \in BC} \right)\) (do \(\angle B'BC\) nhọn).
Trong \(\left( {ABC} \right)\) kẻ \(HK\parallel AC \Rightarrow HK \bot AB\) ta có: \(\left\{ \begin{array}{l}AB \bot HK\\AB \bot B'H\end{array} \right. \Rightarrow AB \bot \left( {B'HK} \right) \Rightarrow AB \bot B'K\).
Ta có: \(\left\{ \begin{array}{l}\left( {ABB'A'} \right) \cap \left( {ABC} \right) = AB\\B'K \subset \left( {ABB'A'} \right),\,\,B'K \bot AB\\HK \subset \left( {ABC} \right),\,\,HK \bot AB\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {ABB'A'} \right);\left( {ABC} \right)} \right) = \angle \left( {B'K;HK} \right) = \angle B'HK = {45^0}\).
\( \Rightarrow \Delta B'HK\) vuông cân tại \(H \Rightarrow B'H = HK = x\).
Xét tam giác vuông \(BB'H\) có: \(BH = \sqrt {BB{'^2} - BH{'^2}} = \sqrt {4{a^2} - {x^2}} \).
Xét tam giác vuông \(ABC\) có: \(AC = BC.\sin {60^0} = a\sqrt 3 \), \(AB = BC.\cos {60^0} = a\).
Áp dụng định lí Ta-lét ta có: \(\dfrac{{BH}}{{BC}} = \dfrac{{HK}}{{AC}} \Rightarrow \dfrac{{\sqrt {4{a^2} - {x^2}} }}{{2a}} = \dfrac{x}{{a\sqrt 3 }}\)
\(\begin{array}{l} \Leftrightarrow 3\left( {4{a^2} - {x^2}} \right) = 4{x^2}\\ \Leftrightarrow 12{a^2} - 3{x^2} = 4{x^2}\\ \Leftrightarrow {x^2} = \dfrac{{12{a^2}}}{7}\\ \Leftrightarrow x = \dfrac{{2a\sqrt {21} }}{7} = B'H\end{array}\)
\({S_{\Delta ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.a.a\sqrt 3 = \dfrac{{{a^2}\sqrt 3 }}{2}\).
Vậy \({V_{ABC.A'B'C'}} = B'H.{S_{\Delta ABC}} = \dfrac{{2a\sqrt {21} }}{7}.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{3{a^3}\sqrt 7 }}{7}\).
Đề thi liên quan
-
Đề kiểm tra 15 phút chương 5: Khối đa diện và thể tích - Đề số 1
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 15 phút chương 5: Khối đa diện và thể tích - Đề số 2
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 15 phút chương 5: Khối đa diện và thể tích - Đề số 3
-
12 câu hỏi
-
45 phút
-
-
Đề kiểm tra 1 tiết chương 5: Khối đa diện và thể tích - Đề số 1
-
25 câu hỏi
-
45 phút
-
-
Đề kiểm tra 1 tiết chương 5: Khối đa diện và thể tích - Đề số 2
-
25 câu hỏi
-
45 phút
-

