Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\)có \(AB = a,\) đường thẳng \(A'B\) tạo với mặt phẳng \(\left( {BCC'B'} \right)\) một góc \({30^0}.\) Tính thể tích khối lăng trụ \(ABC.A'B'C'.\)
A.
\(\dfrac{{3{a^3}}}{2}\)
B.
\(\dfrac{{{a^3}\sqrt 6 }}{4}\)
C.
\(\dfrac{{3{a^3}}}{4}\)
D.
\(\dfrac{{{a^3}\sqrt 3 }}{4}\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: b
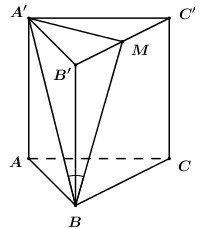
Gọi \(M\) là trung điểm của \(B'C'\). Vì \(\Delta A'B'C'\) đều nên \(A'M \bot B'C'\).
Ta có: \(\left\{ \begin{array}{l}A'M \bot B'C'\\A'M \bot BB'\,\,\left( {BB' \bot \left( {A'B'C'} \right)} \right)\end{array} \right.\) \( \Rightarrow A'M \bot \left( {BCC'B'} \right)\).
\( \Rightarrow BM\) là hình chiếu của \(A'M\) lên \(\left( {BCC'B'} \right)\) \( \Rightarrow \angle \left( {A'B;\left( {BCC'B'} \right)} \right) = \angle \left( {A'B;MB} \right) = \angle A'BM = {30^0}\).
Theo bài ra ta có \(\Delta A'B'C'\) đều cạnh \(a\) nên \(A'M = \dfrac{{a\sqrt 3 }}{2}\) và \({S_{\Delta A'B'C'}} = \dfrac{{{a^2}\sqrt 3 }}{4}\).
Ta có: \(A'M \bot \left( {BCC'B'} \right) \Rightarrow A'M \bot BM\) \( \Rightarrow \Delta A'BM\) vuông tại \(M\) \( \Rightarrow BM = A'M.\cot {30^0} = \dfrac{{3a}}{2}\).
Áp dụng định lí Pytago trong tam giác vuông \(BB'M\) ta có: \(BB' = \sqrt {B{M^2} - BB{'^2}} = \sqrt {{{\left( {\dfrac{{3a}}{2}} \right)}^2} - {{\left( {\dfrac{a}{2}} \right)}^2}} = a\sqrt 2 \).
Vậy \({V_{ABC.A'B'C'}} = BB'.{S_{A'B'C'}} = a\sqrt 2 .\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 6 }}{4}\).
Hướng dẫn giải:
- Xác định góc giữa \(A'B\) và \(\left( {BCC'B'} \right)\) là góc giữa \(A'B\) và hình chiếu của \(A'B\) lên \(\left( {BCC'B'} \right)\).
- Sử dụng công thức tính nhanh: Chiều cao của tam giác đều cạnh \(a\) là \(\dfrac{{a\sqrt 3 }}{2}\) và diện tích tam giác đều cạnh \(a\) là \(\dfrac{{{a^2}\sqrt 3 }}{4}\).
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông và định lí Pytago để tính chiều cao của khối lăng trụ.
- Sử dụng công thức tính thể tích khối lăng trụ có chiều cao \(h\), diện tích đáy \(B\) là \(V = B.h\).

Gọi \(M\) là trung điểm của \(B'C'\). Vì \(\Delta A'B'C'\) đều nên \(A'M \bot B'C'\).
Ta có: \(\left\{ \begin{array}{l}A'M \bot B'C'\\A'M \bot BB'\,\,\left( {BB' \bot \left( {A'B'C'} \right)} \right)\end{array} \right.\) \( \Rightarrow A'M \bot \left( {BCC'B'} \right)\).
\( \Rightarrow BM\) là hình chiếu của \(A'M\) lên \(\left( {BCC'B'} \right)\) \( \Rightarrow \angle \left( {A'B;\left( {BCC'B'} \right)} \right) = \angle \left( {A'B;MB} \right) = \angle A'BM = {30^0}\).
Theo bài ra ta có \(\Delta A'B'C'\) đều cạnh \(a\) nên \(A'M = \dfrac{{a\sqrt 3 }}{2}\) và \({S_{\Delta A'B'C'}} = \dfrac{{{a^2}\sqrt 3 }}{4}\).
Ta có: \(A'M \bot \left( {BCC'B'} \right) \Rightarrow A'M \bot BM\) \( \Rightarrow \Delta A'BM\) vuông tại \(M\) \( \Rightarrow BM = A'M.\cot {30^0} = \dfrac{{3a}}{2}\).
Áp dụng định lí Pytago trong tam giác vuông \(BB'M\) ta có: \(BB' = \sqrt {B{M^2} - BB{'^2}} = \sqrt {{{\left( {\dfrac{{3a}}{2}} \right)}^2} - {{\left( {\dfrac{a}{2}} \right)}^2}} = a\sqrt 2 \).
Vậy \({V_{ABC.A'B'C'}} = BB'.{S_{A'B'C'}} = a\sqrt 2 .\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 6 }}{4}\).
Hướng dẫn giải:
- Xác định góc giữa \(A'B\) và \(\left( {BCC'B'} \right)\) là góc giữa \(A'B\) và hình chiếu của \(A'B\) lên \(\left( {BCC'B'} \right)\).
- Sử dụng công thức tính nhanh: Chiều cao của tam giác đều cạnh \(a\) là \(\dfrac{{a\sqrt 3 }}{2}\) và diện tích tam giác đều cạnh \(a\) là \(\dfrac{{{a^2}\sqrt 3 }}{4}\).
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông và định lí Pytago để tính chiều cao của khối lăng trụ.
- Sử dụng công thức tính thể tích khối lăng trụ có chiều cao \(h\), diện tích đáy \(B\) là \(V = B.h\).
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\). Biết \(AC = a\sqrt 2 \), cạnh \(SC\) tạo với đáy một góc \({60^0}\) và diện tích tứ giác \(ABCD\) là \(\dfrac{{3{a^2}}}{2}\). Gọi \(H\) là hình chiếu của \(A\) trên cạnh \(SC\). Tính thể tích khối chóp \(H.ABCD\).
Trong một hình đa diện lồi, mỗi cạnh là cạnh chung của tất cả bao nhiêu mặt?
Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $a$ và mặt bên hợp với đáy một góc \({60^0}\). Thể tích khối chóp $S.ABC$ là:
Cho hình lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(A.\) Cạnh \(BC = 2a\) và \(\angle ABC = {60^0}.\) Biết tứ giác \(BCC'B'\) là hình thoi có \(\angle B'BC\) nhọn. Mặt phẳng \(\left( {BCC'B'} \right)\) vuông góc với \(\left( {ABC} \right)\) và mặt phẳng \(\left( {ABB'A'} \right)\) tạo với \(\left( {ABC} \right)\) góc \({45^0}.\) Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng:
Đề thi THPT QG - 2021 - mã 101
Cho khối hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy là hình vuông, \(BD = 2a,\) góc giữa hai mặt phẳng \(\left( {A'B{\rm{D}}} \right)\) và \(\left( {ABCD} \right)\) bằng \({30^0}\). Thể tích của khối hộp chữ nhật đã cho bằng
Cho lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác đều cạnh $a$, và \(A'A = A'B = A'C = a\sqrt {\dfrac{7}{{12}}} \) . Thể tích khối lăng trụ \(ABC.A'B'C'\) theo $a$ là:
Cho hình lăng trụ \(ABC.A'B'C'\) có \(AB = 2a,AC = a,AA' = \dfrac{{a\sqrt {10} }}{2},\widehat {BAC} = {120^0}\). Hình chiếu vuông góc của $C’$ lên $(ABC)$ là trung điểm của cạnh $BC$. Tính thể tích khối lăng trụ \(ABC.A'B'C'\) theo $a$?
Khối chóp tam giác có độ dài 3 cạnh xuất phát từ một đỉnh là \(a,\,\,2a,\,\,3a\) có thể tích lớn nhất bằng
Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \({V_1};{V_2}\) lần lượt là thể tích của khối tứ diện \(ACB'D'\) và khối hộp \(ABCD.A'B'C'D'.\) Tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\) bằng
Khối đa diện lồi có \(8\) đỉnh và \(6\) mặt thì có số cạnh là:
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(A,\,\,AB = a,\) cạnh bên \(SC = 3a\) và \(SC\) vuông góc với mặt phẳng đáy. Thể tích khối chóp \(S.ABC\) bằng:
Cho hình chóp \(S.\,ABC\) có \(SA\) vuông góc với đáy. Tam giác \(ABC\) vuông cân tại \(B\), biết \(SA = AC = 2a\). Thể tích khối chóp \(S.ABC\) là