Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
Hỏi bàiĐề kiểm tra 15 phút chương 5: Khối đa diện và thể tích - Đề số 3
-
Hocon247
-
12 câu hỏi
-
45 phút
-
623 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Cho khối chóp có thể tích \(V\), diện tích đáy là \(S\) và chiều cao \(h\). Chọn công thức đúng:
Công thức tính thể tích khối chóp \(V = \dfrac{1}{3}Sh\).
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án D vì nhớ nhầm công thức.
Trong các mệnh đề sau, mệnh đề nào đúng?
Hình đa diện luôn có số đỉnh và số mặt nhỏ hơn số cạnh
Không phải hình đa diện nào cũng có số đỉnh bằng số mặt, ví dụ hình lập phương có 8 đỉnh và 6 mặt
Hình tứ diện có số đỉnh bằng số mặt (bằng 4).
Hướng dẫn giải:
Sử dụng định nghĩa hình đa diện và lấy ví dụ cho những hình đa diện quen thuộc.
Giải thích thêm:
Một số em sẽ chọn đáp án C khi lấy ví dụ tứ diện mà không chú ý đến trường hợp hình hộp.
Cho hình chóp đều $S.ABCD$ có diện tích đáy là \(16c{m^2}\), diện tích một mặt bên là \(8\sqrt 3 c{m^2}\). Thể tích khối chóp $S.ABCD$ là:
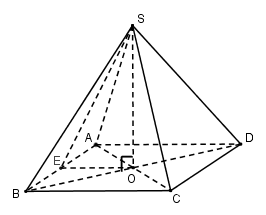
Gọi \(O = AC \cap BD\). Vì chóp $S.ABCD$ đều nên \(SO \bot \left( {ABCD} \right)\)
Vì chóp $S.ABCD$ đều nên $ABCD$ là hình vuông \( \Rightarrow {S_{ABCD}} = A{B^2} = 16 \Rightarrow AB = 4\left( {cm} \right) = AD\)
Gọi $E$ là trung điểm của AB\( \Rightarrow OE\) là đường trung bình của tam giác ABD\( \Rightarrow OE//AD \Rightarrow OE \bot AB\) và \(OE = \dfrac{1}{2}AD = \dfrac{1}{2}.4 = 2\left( {cm} \right)\)
\(\left. \begin{array}{l}OE \bot AB\\SO \bot AB\,\,\left( {SO \bot \left( {ABCD} \right)} \right)\end{array} \right\} \Rightarrow AB \bot \left( {SOE} \right) \Rightarrow AB \bot SE\)
\( \Rightarrow {S_{\Delta SAB}} = \dfrac{1}{2}SE.AB = 8\sqrt 3 \Rightarrow SE = \dfrac{{16\sqrt 3 }}{{AB}} = \dfrac{{16\sqrt 3 }}{4} = 4\sqrt 3 \left( {cm} \right)\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OE \Rightarrow \Delta SOE\) vuông tại O\( \Rightarrow SO = \sqrt {S{E^2} - O{E^2}} = \sqrt {48 - 4} = \sqrt {44} = 2\sqrt {11} \left( {cm} \right)\)
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}.2\sqrt {11} .16 = \dfrac{{32\sqrt {11} }}{3}\left( {c{m^3}} \right)\)
Hướng dẫn giải:
- Gọi \(E\) là trung điểm của \(AB\), tính \(OE,SE \Rightarrow SO\).
- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\).
Một khối chóp có đáy là đa giác $n$ cạnh. Trong các mệnh đề sau đây, mệnh đề nào đúng?
Khối chóp có đáy là đa giác $n$ cạnh thì có $n + 1$ đỉnh (gồm đỉnh $S$ và $n$ đỉnh của đa giác đáy),
$n + 1$ mặt ($1$ mặt đáy và $n$ mặt bên) và $2n$ cạnh ($n$ cạnh bên và $n$ cạnh đáy)
Do đó chỉ có ý A đúng.
Hướng dẫn giải:
Sử dụng định nghĩa khối chóp, tìm số đỉnh, số mặt, số cạnh và đối chiếu đáp án.
Giải thích thêm:
Một số em sẽ chọn đáp án B vì chỉ số đỉnh của mặt đáy mà quên mất đỉnh của khối chóp.
Cho hình lập phương \(ABCD.A'B'C'D'\) có thể tích bằng \(8{a^3}\). Khi đó độ dài cạnh hình lập phương đã cho bằng
Độ dài cạnh hình lập phương đã cho bằng \(2a\).
Hướng dẫn giải:
Thể tích khối lập phương có cạnh a là: \({a^3}\).
Khối đa diện lồi có \(8\) đỉnh và \(6\) mặt thì có số cạnh là:
Ta có: \(D = 8,M = 6\) thì \(D - C + M = 2 \Leftrightarrow 8 - C + 6 = 2 \Leftrightarrow C = 12\)
Vậy số cạnh là \(12\).
Hướng dẫn giải:
Sử dụng định lý Ơ le cho khối đa diện lồi \(D - C + M = 2\)
Đa diện đều loại \(\left\{ {5;3} \right\}\) có tên gọi nào dưới đây?
Đa diện đều loại \(\left\{ {5;3} \right\}\) có tên gọi là Mười hai mặt đều.
Hướng dẫn giải:
Khối đa diện đều loại \(\left\{ {p;q} \right\}\) là khối đa diện lồi thỏa mãn mỗi mặt của nó là đa giác đều \(p\) cạnh và mỗi đỉnh của nó là đỉnh chung của đúng \(q\) mặt.
Cho khối lăng trụ tam giác $ABC.A'B'C'$ mà mặt bên $ABB'A'$ có diện tích bằng $4$. Khoảng cách giữa $CC'$ và mặt phẳng $\left( {ABB'A'} \right)$ bằng $7$. Thể tích khối lăng trụ là:
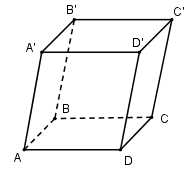
Dựng khối hộp $ABCD.A’B’C’D’$ ta có: \({V_{ABC.A'B'C'}} = \dfrac{1}{2}{V_{ABCD.A'B'C'D'}}\)
Khối hộp \(ABCD.A'B'C'D'\) có hai đáy là $ABB’A’$ và $CDD’C’$
\( \Rightarrow {V_{ABCD.A'B'C'D'}} = {S_{ABB'A'}}.h\)
Trong đó \(h = d\left( {\left( {ABB'A'} \right);\left( {CDD'C'} \right)} \right) = d\left( {CC';\left( {ABB'A'} \right)} \right) = 7\)
\( \Rightarrow {V_{ABCD.A'B'C'D'}} = 4.7 = 28\)
Vậy \({V_{ABC.A'B'C'}} = \dfrac{1}{2}.28 = 14\)
Hướng dẫn giải:
- Dựng khối hộp từ lăng trụ tam giác đã cho.
- Tính thể tích khối hộp dựng được và suy ra thể tích khối lăng trụ tam giác cần tính.
Khối đa diện đều loại \(\left\{ {n;p} \right\}\) thì \(n\) là:
- Khối đa diện đều loại \(\left\{ {n;p} \right\}\):
+ \(n\) là số cạnh của mỗi mặt.
+ \(p\) là số cạnh cùng đi qua một đỉnh.
Vì số đỉnh mỗi mặt bằng số cạnh mỗi mặt nên \(n\) cũng số đỉnh mỗi mặt.
Giải thích thêm:
Với một số em không nhớ kĩ định nghĩa \(n,p\) thì sẽ chọn nhầm đáp án D là sai.
Mệnh đề nào sau đây là mệnh đề đúng?
Đa diện đều có tất cả các mặt là các đa giác bằng nhau.
Không tồn tại đa diện đều có $5$ và $6$ đỉnh, do đó chóp $S.ABCD$ và lăng trụ $ABC.A'B'C'$ không thể là đa diện đều.
Nếu mỗi đỉnh là đỉnh chung của đúng $3$ mặt thì nó cũng là đỉnh chung của đúng $3$ cạnh. Giả sử số đỉnh của đa diện là $n$ thì số cạnh của nó phải là $\dfrac{{3n}}{2}$ (vì mỗi cạnh được tính $2$ lần), do đó $n$ chẵn.
Cho hình chóp \(S.ABC\) đáy \(ABC\) là tam giác vuông tại \(A,AB = a,AC = a\sqrt 3 \). Tam giác $SBC$ đều nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp $S.ABC$
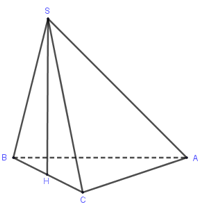
Trong $mp(SBC)$ kẻ \(SH \bot BC\left( {H \in BC} \right) \Rightarrow SH \bot \left( {ABC} \right),H\) là trung điểm \(BC\)
Xét tam giác vuông $ABC$ có \(BC = \sqrt {{a^2} + 3{a^2}} = 2a \Rightarrow \Delta SBC\) đều cạnh $2a$
\( \Rightarrow SH = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SH.{S_{\Delta ABC}} = \dfrac{1}{6}SH.AB.AC = \dfrac{1}{2}{a^3}\)
Hướng dẫn giải:
Bước 1: Xác định chiều cao hình chóp
Bước 2: Áp dụng công thức tính thể tích hình chóp
Cho đa diện \(ABCDEF\) có \(AD,BE,CF\) đôi một song song. \(AD \bot \left( {ABC} \right)\), \(AD + BE + CF = 5\), diện tích tam giác \(ABC\) bằng \(10\). Thể tích đa diện \(ABCDEF\) bằng
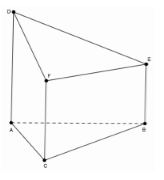
Chọn \(AD = BE = CF = \dfrac{5}{3}\) thì đa diện là hình lăng trụ đứng \(ABC.DEF\) có diện tích đáy \({S_{ABC}} = 10\) và chiều cao \(AD = \dfrac{5}{3}\).
Thể tích \(V = {S_{ABC}}.AD = 10.\dfrac{5}{3} = \dfrac{{50}}{3}\).
Hướng dẫn giải:
Chọn điểm rơi: chọn \(AD = BE = CF = \dfrac{5}{3}\) và tính thể tích khối lăng trụ tam giác theo công thức \(V = Bh\) với \(B\) là diện tích đáy, \(h\) là chiều cao.
