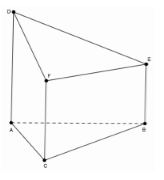
Cho đa diện \(ABCDEF\) có \(AD,BE,CF\) đôi một song song. \(AD \bot \left( {ABC} \right)\), \(AD + BE + CF = 5\), diện tích tam giác \(ABC\) bằng \(10\). Thể tích đa diện \(ABCDEF\) bằng
A.
\(50\)
B.
\(\dfrac{{15}}{2}\)
C.
\(\dfrac{{50}}{3}\)
D.
\(\dfrac{{15}}{4}\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: c
Chọn \(AD = BE = CF = \dfrac{5}{3}\) thì đa diện là hình lăng trụ đứng \(ABC.DEF\) có diện tích đáy \({S_{ABC}} = 10\) và chiều cao \(AD = \dfrac{5}{3}\).
Thể tích \(V = {S_{ABC}}.AD = 10.\dfrac{5}{3} = \dfrac{{50}}{3}\).
Hướng dẫn giải:
Chọn điểm rơi: chọn \(AD = BE = CF = \dfrac{5}{3}\) và tính thể tích khối lăng trụ tam giác theo công thức \(V = Bh\) với \(B\) là diện tích đáy, \(h\) là chiều cao.
Chọn \(AD = BE = CF = \dfrac{5}{3}\) thì đa diện là hình lăng trụ đứng \(ABC.DEF\) có diện tích đáy \({S_{ABC}} = 10\) và chiều cao \(AD = \dfrac{5}{3}\).
Thể tích \(V = {S_{ABC}}.AD = 10.\dfrac{5}{3} = \dfrac{{50}}{3}\).
Hướng dẫn giải:
Chọn điểm rơi: chọn \(AD = BE = CF = \dfrac{5}{3}\) và tính thể tích khối lăng trụ tam giác theo công thức \(V = Bh\) với \(B\) là diện tích đáy, \(h\) là chiều cao.
CÂU HỎI CÙNG CHỦ ĐỀ
Đa diện đều loại \(\left\{ {5;3} \right\}\) có tên gọi nào dưới đây?
Cho khối lăng trụ tam giác $ABC.A'B'C'$ mà mặt bên $ABB'A'$ có diện tích bằng $4$. Khoảng cách giữa $CC'$ và mặt phẳng $\left( {ABB'A'} \right)$ bằng $7$. Thể tích khối lăng trụ là:
Cho khối chóp có thể tích \(V\), diện tích đáy là \(S\) và chiều cao \(h\). Chọn công thức đúng:
Cho hình lập phương \(ABCD.A'B'C'D'\) có thể tích bằng \(8{a^3}\). Khi đó độ dài cạnh hình lập phương đã cho bằng
Cho hình chóp đều $S.ABCD$ có diện tích đáy là \(16c{m^2}\), diện tích một mặt bên là \(8\sqrt 3 c{m^2}\). Thể tích khối chóp $S.ABCD$ là:
Một khối chóp có đáy là đa giác $n$ cạnh. Trong các mệnh đề sau đây, mệnh đề nào đúng?
Cho hình chóp \(S.ABC\) đáy \(ABC\) là tam giác vuông tại \(A,AB = a,AC = a\sqrt 3 \). Tam giác $SBC$ đều nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp $S.ABC$
Khối đa diện đều loại \(\left\{ {n;p} \right\}\) thì \(n\) là:
Khối đa diện lồi có \(8\) đỉnh và \(6\) mặt thì có số cạnh là:

