Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: c
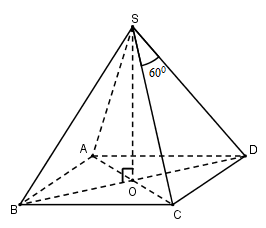
Gọi \(O = AC \cap BD\).
Vì chóp $S.ABCD$ đều nên \(SO \bot \left( {ABCD} \right)\)
Đặt \(SA = SB = SC = SD = a\)
Tam giác $SCD$ có:\(SC = SD;\widehat {CSD} = {60^0} \Rightarrow \Delta SCD\) đều\( \Rightarrow CD = SC = SD = a\)
\( \Rightarrow \) Hình vuông $ABCD$ cạnh \(a \Rightarrow AC = BD = a\sqrt 2 \Rightarrow OC = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OC \Rightarrow \Delta SOC\) vuông tại $O$
\( \Rightarrow SO = \sqrt {S{C^2} - O{C^2}} \Rightarrow h = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 2 }}{2} \Rightarrow a = h\sqrt 2 \)
\( \Rightarrow {S_{ABCD}} = {a^2} = {\left( {h\sqrt 2 } \right)^2} = 2{h^2}\)
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}h.2{h^2} = \dfrac{{2{h^3}}}{3}\)
Hướng dẫn giải:
- Bước 1: Tính diện tích đáy \(S\)
- Bước 2: Tính chiều cao \(h\).
- Bước 3: Tính thể tích \(V = \dfrac{1}{3}Sh\).

Gọi \(O = AC \cap BD\).
Vì chóp $S.ABCD$ đều nên \(SO \bot \left( {ABCD} \right)\)
Đặt \(SA = SB = SC = SD = a\)
Tam giác $SCD$ có:\(SC = SD;\widehat {CSD} = {60^0} \Rightarrow \Delta SCD\) đều\( \Rightarrow CD = SC = SD = a\)
\( \Rightarrow \) Hình vuông $ABCD$ cạnh \(a \Rightarrow AC = BD = a\sqrt 2 \Rightarrow OC = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OC \Rightarrow \Delta SOC\) vuông tại $O$
\( \Rightarrow SO = \sqrt {S{C^2} - O{C^2}} \Rightarrow h = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 2 }}{2} \Rightarrow a = h\sqrt 2 \)
\( \Rightarrow {S_{ABCD}} = {a^2} = {\left( {h\sqrt 2 } \right)^2} = 2{h^2}\)
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}h.2{h^2} = \dfrac{{2{h^3}}}{3}\)
Hướng dẫn giải:
- Bước 1: Tính diện tích đáy \(S\)
- Bước 2: Tính chiều cao \(h\).
- Bước 3: Tính thể tích \(V = \dfrac{1}{3}Sh\).
CÂU HỎI CÙNG CHỦ ĐỀ
Cho tứ diện \(ABCD\) có các cạnh \(AB,AC,AD\) đôi một vuông góc với nhau, \(AB = 6a,AC = 7a,AD = 4a\). Gọi \(M,N,P\) lần lượt là trung điểm của các cạnh \(BC,CD,DB\). Thể tích \(V\) của tứ diện \(AMNP\) là:
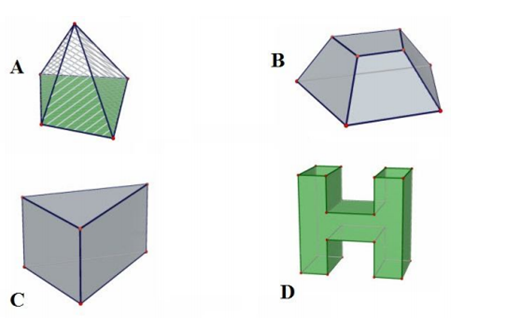
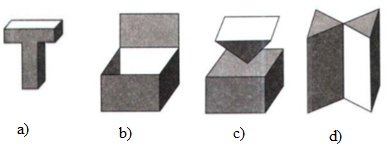
Vật thể nào trong các vật thể sau không phải là khối đa diện?

Trong các hình dưới đây, hình nào là khối đa diện?
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\). Biết \(AC = a\sqrt 2 \), cạnh \(SC\) tạo với đáy một góc \({60^0}\) và diện tích tứ giác \(ABCD\) là \(\dfrac{{3{a^2}}}{2}\). Gọi \(H\) là hình chiếu của \(A\) trên cạnh \(SC\). Tính thể tích khối chóp \(H.ABCD\).
Cho hình chóp \(S.ABC\) có \(SA \bot SB,SB \bot SC,SA \bot SC;SA = 2a,SB = b,SC = c\). Thể tích khối chóp là:
Cho khối đa diện lồi có số đỉnh, số mặt và số cạnh lần lượt là \(D,M,C\). Chọn mệnh đề đúng:
Cho hình chóp đều $S.ABCD$ có cạnh bên và cạnh đáy bằng $a$. Thể tích của khối chóp $S.ABCD$ là:
Cho khối chóp \(S.ABC\). Trên các cạnh \(SA,SB,SC\) lấy các điểm \(A',B',C'\) sao cho \(A'A = 2SA',B'B = 2SB',C'C = 2SC'\), khi đó tồn tại một phép vị tự biến khối chóp \(S.ABC\) thành khối chóp \(S.A'B'C'\) với tỉ số đồng dạng là: