Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình thang vuông tại \(A\) và \(D\) thỏa mãn \(SA \bot \left( {ABCD} \right)\) và \(AB = 2AD = 2CD = 2a = \sqrt 2 SA\). Thể tích khối chóp \(S.BCD\) là:
A.
\(\dfrac{{2{a^3}\sqrt 2 }}{3}\)
B.
\(\dfrac{{{a^3}\sqrt 2 }}{6}\)
C.
\(\dfrac{{2{a^3}}}{3}\)
D.
\(\dfrac{{{a^3}\sqrt 2 }}{{12}}\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: b
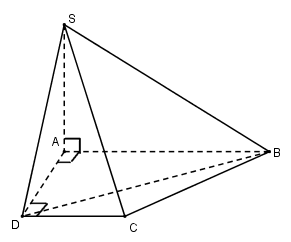
Ta có: \({S_{ABCD}} = \dfrac{1}{2}\left( {AB + CD} \right).AD = \dfrac{1}{2}\left( {2a + a} \right)a = \dfrac{{3{a^2}}}{2}\)
\({S_{\Delta ABD}} = \dfrac{1}{2}AD.AB = \dfrac{1}{2}a.2a = {a^2}\)
\( \Rightarrow {S_{BCD}} = {S_{ABCD}} - {S_{ABD}} = \dfrac{{3{a^2}}}{2} - {a^2} = \dfrac{{{a^2}}}{2}\)
\(SA = \dfrac{{2a}}{{\sqrt 2 }} = a\sqrt 2 \)
\( \Rightarrow {V_{S.BCD}} = \dfrac{1}{3}SA.{S_{BCD}} = \dfrac{1}{3}a\sqrt 2 .\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}\sqrt 2 }}{6}\)
Hướng dẫn giải:
- Bước 1: Tính diện tích đáy \({S_{\Delta BCD}}\), dựa vào các tính chất của đáy.
- Bước 2: Tính chiều cao \(h = SA\).
- Bước 3: Tính thể tích khối chóp \(V = \dfrac{1}{3}Sh\).
Giải thích thêm:
Một số em sẽ tính nhầm \(SA = \dfrac{{a\sqrt 2 }}{2}\) dẫn đến chọn nhầm đáp án D là sai.

Ta có: \({S_{ABCD}} = \dfrac{1}{2}\left( {AB + CD} \right).AD = \dfrac{1}{2}\left( {2a + a} \right)a = \dfrac{{3{a^2}}}{2}\)
\({S_{\Delta ABD}} = \dfrac{1}{2}AD.AB = \dfrac{1}{2}a.2a = {a^2}\)
\( \Rightarrow {S_{BCD}} = {S_{ABCD}} - {S_{ABD}} = \dfrac{{3{a^2}}}{2} - {a^2} = \dfrac{{{a^2}}}{2}\)
\(SA = \dfrac{{2a}}{{\sqrt 2 }} = a\sqrt 2 \)
\( \Rightarrow {V_{S.BCD}} = \dfrac{1}{3}SA.{S_{BCD}} = \dfrac{1}{3}a\sqrt 2 .\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}\sqrt 2 }}{6}\)
Hướng dẫn giải:
- Bước 1: Tính diện tích đáy \({S_{\Delta BCD}}\), dựa vào các tính chất của đáy.
- Bước 2: Tính chiều cao \(h = SA\).
- Bước 3: Tính thể tích khối chóp \(V = \dfrac{1}{3}Sh\).
Giải thích thêm:
Một số em sẽ tính nhầm \(SA = \dfrac{{a\sqrt 2 }}{2}\) dẫn đến chọn nhầm đáp án D là sai.
CÂU HỎI CÙNG CHỦ ĐỀ
Công thức nào sau đây không đúng khi tính diện tích toàn phần hình trụ?
Tập hợp tất cả các giá trị của m để hàm số $y = \dfrac{1}{3}{x^3} - \left( {m - 1} \right){x^2} + 2\left( {m - 1} \right)x - 2$ luôn tăng trên $R$
Điều kiện để hàm số bậc ba không có cực trị là phương trình $y' = 0$ có:
Cho hàm số \(y=\dfrac{2x+1}{x-2}\). Khẳng định nào dưới đây là đúng?
Phép đối xứng qua mặt phẳng \(\left( P \right)\) biến điểm \(M,N\) thành \(M',N'\) thì:
Phép vị tự tỉ số \(k > 0\) biến khối chóp có thể tích \(V\) thành khối chóp có thể tích \(V'\). Khi đó:
Cho hình lập phương \(ABCD.A'B'C'D'\) tâm \(O\). Phép dời hình nào không biến hình vuông \(ABCD\) thành hình vuông \(A'B'C'D'\)?
Công thức tính thể tích khối nón biết diện tích đáy \({S_d}\) và đường sinh \(l\) là:
Gọi $m$ là giá trị nhỏ nhất của hàm số $y = x - 1 + \dfrac{4}{{x - 1}}$ trên khoảng $\left( {1; + \infty {\rm{\;}}} \right)$. Tìm $m?$
Tìm số nghiệm nguyên của bất phương trình \({\left( {\dfrac{1}{3}} \right)^{\sqrt {{x^2} - 3x - 10} }} > {\left( {\dfrac{1}{3}} \right)^{x - 2}}\)
Cho hình trụ có bán kính đáy bằng \(a\). Cắt hình trụ bởi một mặt phẳng song song với trục của hình trụ và cách trục của hình trụ một khoảng bằng \(\dfrac{a}{2}\) ta được thiết diện là một hình vuông. Tính thể tích khối trụ.
Số điểm cực trị của hàm số $y = {(x - 1)^{2017}}$ là

