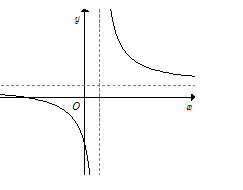
Hàm số $y = \dfrac{{bx - c}}{{x - a}}$ $\left( {a \ne 0;} \right.$ $\left. {a,{\rm{ }}b,{\rm{ }}c \in \mathbb{R}} \right)$ có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng?
A.
\(a > 0,{\rm{ }}b > 0,{\rm{ }}c - ab < 0.\)
B.
\(a > 0,{\rm{ }}b > 0,{\rm{ }}c - ab > 0.\)
C.
\(a > 0,{\rm{ }}b > 0,{\rm{ }}c - ab = 0.\)
D.
\(a > 0,{\rm{ }}b < 0,{\rm{ }}c - ab < 0.\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: a
Đồ thị hàm số có tiệm cận đứng $x = a > 0$; tiệm cận ngang \(y = b > 0.\)
Mặt khác, ta thấy dạng đồ thị là đường cong đi xuống từ trái sang phải trên các khoảng xác định của nó nên
Vậy \(a > 0,{\rm{ }}b > 0,{\rm{ }}c - ab < 0.\)
Hướng dẫn giải:
Tìm các đường tiệm cận của đồ thị hàm số, nhận xét tính đồng biến, nghịch biến rồi suy ra mối quan hệ giữa các hệ số \(a,b,c\)
Đồ thị hàm số có tiệm cận đứng $x = a > 0$; tiệm cận ngang \(y = b > 0.\)
Mặt khác, ta thấy dạng đồ thị là đường cong đi xuống từ trái sang phải trên các khoảng xác định của nó nên
Vậy \(a > 0,{\rm{ }}b > 0,{\rm{ }}c - ab < 0.\)
Hướng dẫn giải:
Tìm các đường tiệm cận của đồ thị hàm số, nhận xét tính đồng biến, nghịch biến rồi suy ra mối quan hệ giữa các hệ số \(a,b,c\)
CÂU HỎI CÙNG CHỦ ĐỀ
Công thức nào sau đây không đúng khi tính diện tích toàn phần hình trụ?
Tập hợp tất cả các giá trị của m để hàm số $y = \dfrac{1}{3}{x^3} - \left( {m - 1} \right){x^2} + 2\left( {m - 1} \right)x - 2$ luôn tăng trên $R$
Điều kiện để hàm số bậc ba không có cực trị là phương trình $y' = 0$ có:
Cho hàm số \(y=\dfrac{2x+1}{x-2}\). Khẳng định nào dưới đây là đúng?
Phép đối xứng qua mặt phẳng \(\left( P \right)\) biến điểm \(M,N\) thành \(M',N'\) thì:
Phép vị tự tỉ số \(k > 0\) biến khối chóp có thể tích \(V\) thành khối chóp có thể tích \(V'\). Khi đó:
Cho hình lập phương \(ABCD.A'B'C'D'\) tâm \(O\). Phép dời hình nào không biến hình vuông \(ABCD\) thành hình vuông \(A'B'C'D'\)?
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình thang vuông tại \(A\) và \(D\) thỏa mãn \(SA \bot \left( {ABCD} \right)\) và \(AB = 2AD = 2CD = 2a = \sqrt 2 SA\). Thể tích khối chóp \(S.BCD\) là:
Gọi $m$ là giá trị nhỏ nhất của hàm số $y = x - 1 + \dfrac{4}{{x - 1}}$ trên khoảng $\left( {1; + \infty {\rm{\;}}} \right)$. Tìm $m?$
Công thức tính thể tích khối nón biết diện tích đáy \({S_d}\) và đường sinh \(l\) là:
Tìm số nghiệm nguyên của bất phương trình \({\left( {\dfrac{1}{3}} \right)^{\sqrt {{x^2} - 3x - 10} }} > {\left( {\dfrac{1}{3}} \right)^{x - 2}}\)
Cho hình trụ có bán kính đáy bằng \(a\). Cắt hình trụ bởi một mặt phẳng song song với trục của hình trụ và cách trục của hình trụ một khoảng bằng \(\dfrac{a}{2}\) ta được thiết diện là một hình vuông. Tính thể tích khối trụ.

