Tứ giác

Lý thuyết về tứ giác, tứ giác lồi, tứ giác đều, định lý về tổng các góc trong tứ giác và phương pháp giải các dạng toán thường gặp Toán 8
(401) 1338 31/07/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    1. Các kiến thức cần nhớ

    Tứ giác

    Định nghĩa : Tứ giác $ABCD$ là một hình gồm bốn đoạn thẳng $AB$ , $BC$ , $CD$ , $DA,$ trong đó bất kỳ hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.

    Tứ giác lồi

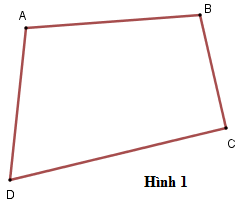
    Định nghĩa: Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào của tứ giác.

    Ví dụ: Tứ giác \(ABCD\) (hình 1) là tứ giác lồi

    Tổng các góc của một tứ giác

    Định lý : Tổng bốn góc của một tứ giác bằng ${360^0}.$

    Ví dụ: Tứ giác \(ABCD\) có \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)

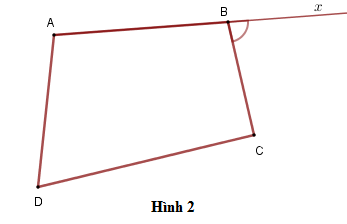
    Chú ý:  Góc ngoài của tứ giác là góc kề bù với một góc của tứ giác.

    Ví dụ: Góc \(CBx\) là góc ngoài tại đỉnh \(B\) của tứ giác \(ABCD\) \( \Rightarrow \widehat {CBx} + \widehat {ABC} = 180^\circ .\) 

    Đa giác đều

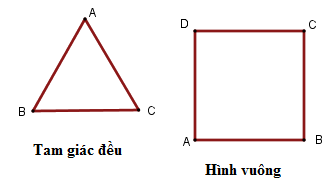
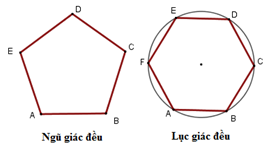
    Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

    2. Các dạng toán thường gặp

    Dạng 1: Sử dụng tính chất về các góc của một tứ giác để tính góc

    Phương pháp:

    Ta sử dụng các kiến thức:

    + Tổng bốn góc của một tứ giác bằng${360^0}$ .

    + Góc ngoài của tứ giác là góc kề bù với một góc của tứ giác.

    Dạng 2: Sử dụng bất đẳng thức tam giác để giải các bài toán liên quan đến các cạnh của một tứ giác

    Phương pháp:

    Ta sử dụng các kiến thức sau:

    + Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.

    + Trong một tam giác, hiệu độ dài hai cạnh bất kì bao giờ cũng nhỏ hơn độ dài cạnh còn lại.

    + Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh còn lại.

    Nghĩa là: Trong tam giác \(ABC\) ta có $\left| {AB-AC} \right| < BC < AB + AC$.

    Xem toàn bộ nội dung Toán 8:

    (401) 1338 31/07/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý thuyết lớp 8 Toán 8