Đường trung bình của tam giác, hình thang

Lý thuyết về đường trung bình của tam giác, đường trung bình hình thang và phương pháp giải các dạng toán về đường trung bình Toán 8
(391) 1303 31/07/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    1. Kiến thức cần nhớ

    Đường trung bình của tam giác

    Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

    Định lý 1: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.

    Định lý 2: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

    Ví dụ:

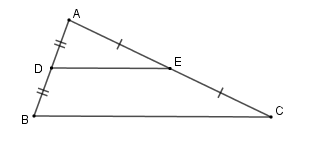
    + \(\Delta ABC\) có \(D\) là trung điểm của \(AB\) , \(E\) là trung điểm của \(AC\) nên \(DE\) là đường trung bình của tam giác \(ABC\) \( \Rightarrow DE{\rm{//}}BC;\,DE = \dfrac{1}{2}BC.\) 

    + Nếu \(\left\{ \begin{array}{l}DA = DB\\DE{\rm{//}}BC\end{array} \right. \Rightarrow EC = EA\) .

    Đường trung bình của hình thang

    Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.

    Định lí 3: Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.

    Định lí 4: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.

    Ví dụ:

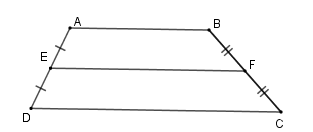
    + Hình thang \(ABCD\) (hình vẽ) có \(E\) là trung điểm \(AD\) , \(F\) là trung điểm của \(BC\) nên \(EF\) là đường trung bình của hình thang \( \Rightarrow \left\{ \begin{array}{l}EF{\rm{//}}DC\\EF = \dfrac{{AB + DC}}{2}\end{array} \right.\)

    2. Các dạng toán thường gặp

    Dạng 1: Chứng minh các hệ thức về cạnh và góc. Tính các cạnh và góc.

    Phương pháp: 

    Sử dụng tính chất đường trung bình của tam giác và hình thang.

    + Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

    + Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.

    + Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.

    + Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.

    Dạng 2: Chứng minh một cạnh là đường trung bình của tam giác, hình thang.

    Phương pháp:

    Sử dụng định nghĩa đường trung bình của tam giác và hình thang.

    + Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

    + Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.

    Xem toàn bộ nội dung Toán 8:

    (391) 1303 31/07/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý thuyết lớp 8 Toán 8