Hình chữ nhật

Lý thuyết về hình chữ nhật và dấu hiệu nhận biết hình chữ nhật, đường thẳng song song cách đều cùng phương pháp giải các dạng toán về hình chữ nhật Toán 8
(401) 1336 31/07/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    I. Các kiến thức cần nhớ

    Định nghĩa: Hình chữ nhật là tứ giác có bốn góc vuông.

    Ví dụ: \(ABCD\) là hình chữ nhật \( \Leftrightarrow \widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \) .

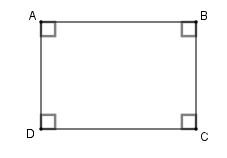
    Chú ý: Hình chữ nhật cũng là một hình bình hành, một hình thang cân.

    Tính chất:

    + Hình chữ nhật có tất cả các tính chất của hình hành, của hình thang cân.

    - Hai cạnh đối song song, hai cạnh đối bằng nhau, hai góc đối bằng nhau

    - Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

    Dấu hiệu nhận biết

    + Tứ giác có ba góc vuông là hình chữ nhật

    + Hình thang cân có một góc vuông là hình chữ nhật.

    + Hình bình hành có một góc vuông là hình chữ nhật

    + Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

    Áp dụng vào tam giác

    Định lí:

    1. Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.

    2. Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.

    Ví dụ:

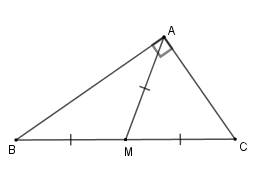
    + Nếu tam giác \(ABC\) vuông tại \(A\) và \(M\) là trung điểm cạnh \(BC \) thì \( AM = BM = CM = \dfrac{{BC}}{2}.\)

    + Nếu tam giác \(ABC\) có \(M\) là trung điểm \(BC\) và \(AM = \dfrac{{BC}}{2}\) thì \(\Delta ABC\) vuông tại \(A.\)

    Đường thẳng song song với một đường thẳng cho trước

    * Định nghĩa: Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thẳng này đến đường thẳng kia.
    Tính chất: Các điểm cách đường thẳng  một khoảng bằng  nằm trên hai đường thẳng song song với và cách  một khoảng bằng
    * Đường thẳng song song cách đều

    Định lí:

    - Nếu các đường thẳng song song cách đều cắt một đường thẳng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.

    - Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.

    II. Các dạng toán thường gặp

    Dạng 1: Vận dụng dấu hiệu nhận biết để chứng minh một tứ giác là hình chữ nhật

    Phương pháp:

    Ta sử dụng các dấu hiệu nhận biết sau:

    + Tứ giác có ba góc vuông là hình chữ nhật

    + Hình thang cân có một góc vuông là hình chữ nhật.

    + Hình bình hành có một góc vuông là hình chữ nhật

    + Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

    Dạng 2: Vận dụng kiến thức hình chữ nhật để chứng minh và tính toán

    Phương pháp:

    Ta sử dụng định nghĩa, định lý và các tính chất của hình chữ nhật để giải toán.

    Xem toàn bộ nội dung Toán 8:

    (401) 1336 31/07/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý thuyết lớp 8 Toán 8