Ôn tập chương 8

I. Sơ đồ Ôn tập chương 8

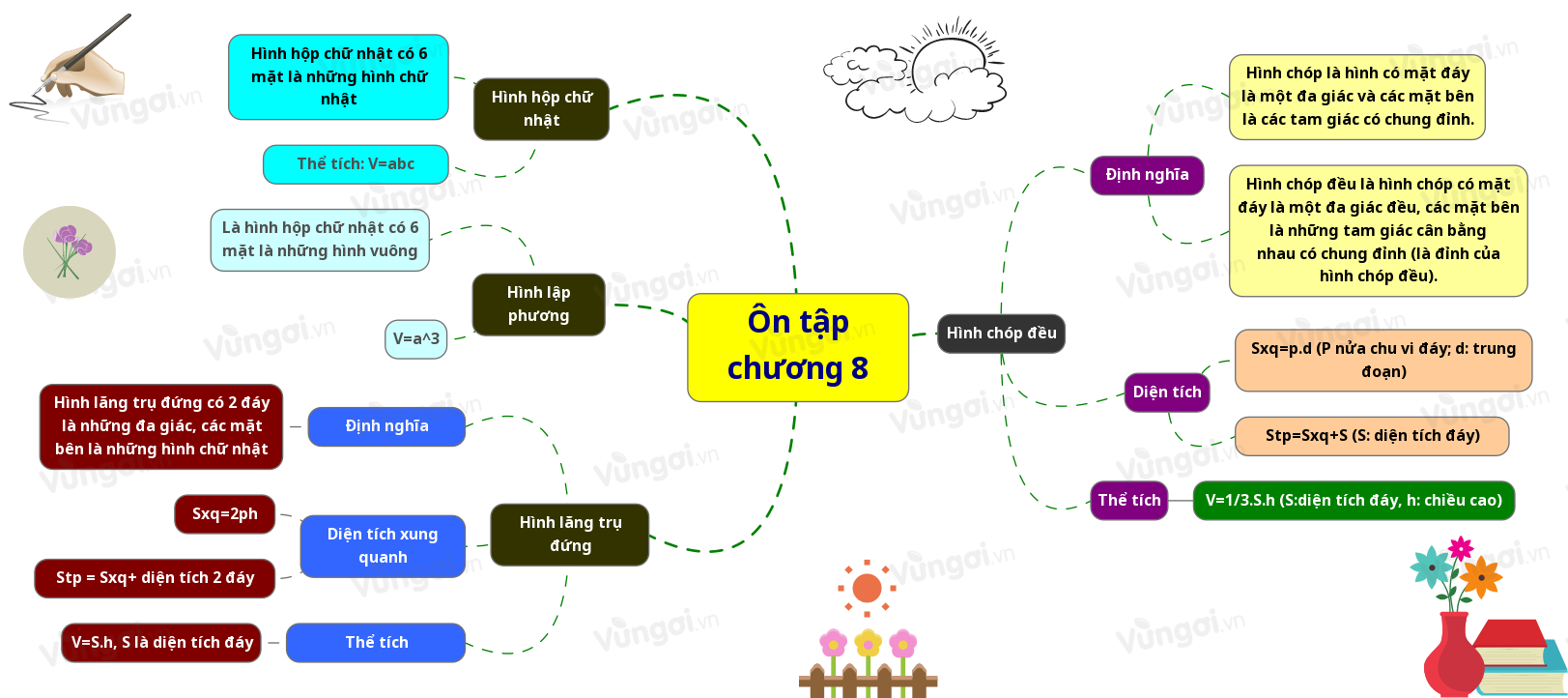
II. Ôn tập chương 8: Hình lăng trụ đứng. Hình chóp đều

1. Hình hộp chữ nhật, hình lập phương

a. Định nghĩa:

Hình hộp chữ nhật có $6$  mặt là những hình chữ nhật .

Hình lập phương là hình hộp chữ nhật có $6$  mặt là những hình vuông

b. Công thức thể tích

2. Đường thẳng và mặt phẳng trong không gian

a) Quan hệ song song

+)  Hai đường thẳng phân biệt trong không gian có các vị trí:

- Cắt nhau nều có một điểm chung

- Song song, nếu cùng nằm trong một mặt phẳng và không có điểm chung

- Không cùng nằm trong một mặt phẳng nào khi đó ta gọi chúng là hai đường thẳng chéo nhau.

+)  Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.

+) Nếu đường thẳng  $\left( a \right)$ không nằm trong mặt phẳng $\left( P \right)$ và song song với một đường thẳng của mp $\left( P \right)$ thì đường thẳng $\left( a \right)$ song song với mp $\left( P \right).$

+) Nếu mặt phẳng $\left( Q \right)$ chứa hai đường thẳng cắt nhau và chúng cùng song song với mp $\left( P \right)$  thì mp $\left( Q \right)$ song song với mp $\left( P \right).$

+)  Hai mặt mặt phẳng phân biệt có các vị trí:

- Song song, nếu chúng không có điểm chung nào.

- Cắt nhau, nếu tồn tại một điểm chung, khi đó chúng cắt nhau theo một đường thẳng đi qua điểm chung đó.

b)  Quan hệ vuông góc

+) Đường thẳng vuông góc với mặt phẳng

- Nếu đường thẳng $\left( a \right)$ vuông góc với hai dường thẳng cắt nhau của mp $\left( P \right)$ thì đường thẳng  $\left( a \right)$ vuông góc với mp $\left( P \right).$

- Nếu đường thẳng $\left( a \right)$ vuông góc với mp $\left( P \right)$ tại điểm $I$  thì nó vuông góc với mọi đường thẳng đi qua $I$ và nằm trong mp $\left( P \right).$

+)  Mặt phẳng vuông góc với mặt phẳng

Nếu mp $\left( Q \right)$ chứa một đường thẳng vuông góc với mp $\left( P \right)$ thì mp $\left( Q \right)$ vuông góc với mp $\left( P \right).$

3. Hình lăng trụ đứng

a) Định nghĩa

+ Hình lăng trụ đứng có hai đáy là những đa giác, các mặt bên là những hình chữ nhật.

+ Các mặt phẳng chứa đáy của hình lăng trụ đứng là các mặt phẳng song song, các mặt bên vuông góc với hai mặt phẳng đáy, các cạnh bên vuông góc với hai mặt phẳng đáy. Độ dài một cạnh bên gọi là chiều cao.

+ Hình lăng trụ đứng có đáy là hình bình hành gọi là hình hộp đứng.

b) Diện tích xung quanh hình lăng trụ đứng

c) Thể tích hình lăng trụ đứng

4. Hình chóp đều, hình chóp cụt đều

a) Đinh nghĩa

+ Hình chóp là hình có mặt đáy là một đa giác và các mặt bên là các tam giác có chung đỉnh.

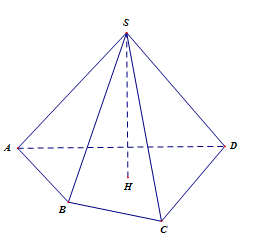
+ Hình chóp đều là hình chóp có mặt đáy là một đa giác đều, các mặt bên là những tam giác cân bằng nhau có chung đỉnh (là đỉnh của hình chóp đều).

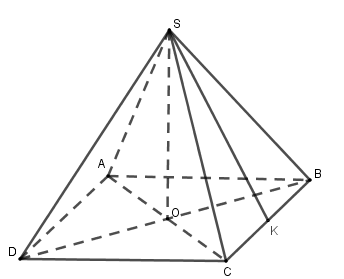
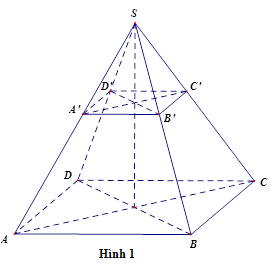
+ Khi cắt hình chóp đều bởi mộ mặt phẳng song song với đáy, phần hình chóp nằm giữa hai mặt phẳng đó và mặt phẳng đáy của hình chóp gọi là hình chóp cụt đều.

Mỗi mặt bên của hình chóp cụt đều là một hình thang cân.

Ở hình 1, ta có hình chóp cụt tứ giác đều $ABCD.A'B'C'D'$.

b. Diện tích xung quanh của hình chóp đều

+ Với hình chóp, để tính diện tích xung quanh ta tính tổng diện tích của các mặt bên.

+  Để tính diện tích xung quanh của hình chóp cụt đều, ta tính diện tích một mặt bên rồi nhân với số mặt bên, hoặc lấy diện tích xung quanh của hình chóp đều lớn trừ đi diện tích xung quanh của hình chóp đều nhỏ.

c. Thể tích hình chóp đều