Tổng hợp dao động - Phương pháp giải bài tập tổng hợp dao động điều hòa
I- NỘI DUNG LÍ THUYẾT
Mỗi dao động điều hòa được biểu diễn bằng một véctơ quay. Véctơ này có gốc tại gốc tọa độ của trục Ox, có độ dài bằng biên độ dao động A và hợp với trục Ox một góc bằng pha ban đầu \(\varphi \) .
- Tổng hợp hai dao động điều hòa cùng phương cùng tần số - Phương pháp giản đồ Fre-nen: Lần lượt vẽ hai véctơ quay biểu diễn hai phương trình dao động thành phần. Sau đó vẽ véctơ tổng của hai véctơ trên. Véctơ tổng la véctơ quay biểu diễn phương trình của dao động tổng hợp.
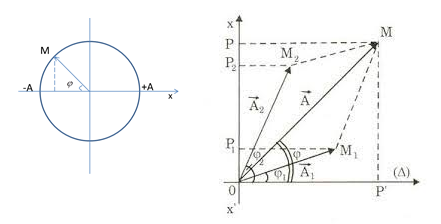
- Biên độ và pha ban đầu của dao động tổng hợp:
\(\begin{array}{l}{A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}{\rm{cos(}}{\varphi _2} - {\varphi _1})\\tan\varphi = \dfrac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}{\rm{cos}}{\varphi _1} + {A_2}{\rm{cos}}{\varphi _2}}}\end{array}\)
Trường hợp độ lệch pha của hai dao động đặc biệt:
- \(\Delta \varphi = {\varphi _2} - {\varphi _1} = k2\pi \): hai dao động cùng pha
\(\begin{array}{l}{A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2} = {({A_1} + {A_2})^2}\\ \to A = {A_1} + {A_2}\end{array}\)
- \(\Delta \varphi = {\varphi _2} - {\varphi _1} = (2k + 1)\pi \): hai dao động ngược pha
\(\begin{array}{l}{A^2} = A_1^2 + A_2^2 - 2{A_1}{A_2} = {({A_1} - {A_2})^2}\\ \to A = \left| {{A_1} - {A_2}} \right|\end{array}\)
- \(\Delta \varphi = {\varphi _2} - {\varphi _1} = \dfrac{{2k + 1}}{2}\pi \) : hai dao động vuông pha
\({A^2} = A_1^2 + A_2^2\)
=> Điều kiện của biên độ tổng hợp A:
\({A_{\min }} \le A \le {A_{\max }} \Leftrightarrow \left| {{A_1} - {A_2}} \right| \le A \le {A_1} + {A_2}\)
II- CÁC DẠNG BÀI TẬP
1. Dạng 1: Xác định độ lệch pha của hai dao động.
Phương pháp
\(\Delta \varphi = {\varphi _2} - {\varphi _1}\)
- \(\Delta \varphi = {\varphi _2} - {\varphi _1} = k2\pi \): hai dao động cùng pha
- \(\Delta \varphi = {\varphi _2} - {\varphi _1} = (2k + 1)\pi \): hai dao động ngược pha
- \(\Delta \varphi = {\varphi _2} - {\varphi _1} = \dfrac{{2k + 1}}{2}\pi \) : hai dao động vuông pha
- \(\Delta \varphi = {\varphi _2} - {\varphi _1} = \alpha \) : hai dao động lệch nhau một góc α
2. Dạng 2: Xác định dao động tổng hợp của hai dao động điều hòa.
Phương pháp
Cách 1: Phương pháp đại số
- Bước 1: Xác định các biên độ thành phần của hai dao động và độ lệch pha giữa hai dao động.
- Bước 2: Tính biên độ và pha ban đầu của dao động tổng hợp:
\(\begin{array}{l}{A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}{\rm{cos(}}{\varphi _2} - {\varphi _1})\\tan\varphi = \dfrac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}{\rm{cos}}{\varphi _1} + {A_2}{\rm{cos}}{\varphi _2}}}\end{array}\)
- Bước 3: Viết ptdđ tổng hợp: \(x = Ac{\rm{os(}}\omega {\rm{t + }}\varphi {\rm{)}}\)
Cách 2: Sử dụng máy tính
Bấm máy tính: Chuyển máy tính về CMPLX (bấm Mode 2); Nhập số:
\({A_1}\angle {\varphi _1} + {A_2}\angle {\varphi _2}\, = \,shift\,2\,\,\,3\,\, = \) Kết quả: \(A\angle \varphi \)
3. Dạng 3: Xác định dao động còn lại khi biết một dao động thành phần \({{\bf{x}}_{\bf{1}}} = {{\bf{A}}_{\bf{1}}}{\bf{cos}}(\omega {\bf{t}}{\rm{ }} + {\varphi _{\bf{1}}})\) và dao động tổng hợp \({\bf{x}}{\rm{ }} = {\rm{ }}{\bf{Acos}}(\omega {\bf{t}}{\rm{ }} + \varphi )\)
Phương pháp
\({x_2} = {A_2}cos(\omega t{\rm{ }} + {\varphi _2}).\)
Trong đó:
- \(A_2^2 = {A^2} + A_1^2 - 2A{A_1}c{\rm{os}}(\varphi - {\varphi _1})\)
- \(\tan {\varphi _2} = \dfrac{{A\sin \varphi - {A_1}\sin {\varphi _1}}}{{Ac{\rm{os}}\varphi - {A_1}c{\rm{os}}{\varphi _1}}}\) với \({\varphi _1} \le \varphi \le {\varphi _2}\) ( nếu \(\varphi 1{\rm{ }} \le \varphi 2\) )
4. Dạng 4: Nếu một vật tham gia đồng thời nhiều dao động điều hoà cùng phương cùng tần số \({{\bf{x}}_{\bf{1}}} = {{\bf{A}}_{\bf{1}}}{\bf{cos}}(\omega {\bf{t}}{\rm{ }} + {\varphi _{\bf{1}}});{{\bf{x}}_{\bf{2}}} = {{\bf{A}}_{\bf{2}}}{\bf{cos}}(\omega {\bf{t}}{\rm{ }} + {\varphi _{\bf{2}}})\) … thì dao động tổng hợp cũng là dao động điều hoà cùng phương cùng tần số
Phương pháp
\(x{\rm{ }} = {\rm{ }}Acos(\omega t{\rm{ }} + \varphi ).\)
Chiếu lên trục Ox và trục Oy
Ta được:
\({A_x} = Ac{\rm{os}}\varphi = {A_1}c{\rm{os}}{\varphi _1} + {A_2}c{\rm{os}}{\varphi _2} + ...\)
\({A_y} = A\sin \varphi = {A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2} + ...\)
\( \Rightarrow A = \sqrt {A_x^2 + A_y^2} \) và \(\tan \varphi = \dfrac{{{A_y}}}{{{A_x}}}\) với \(\varphi \in ({\varphi _{Min}};{\varphi _{Max}})\)
