Sóng dừng
I. Bảng tổng hợp lý thuyết sự phản xạ của sóng - sóng dừng
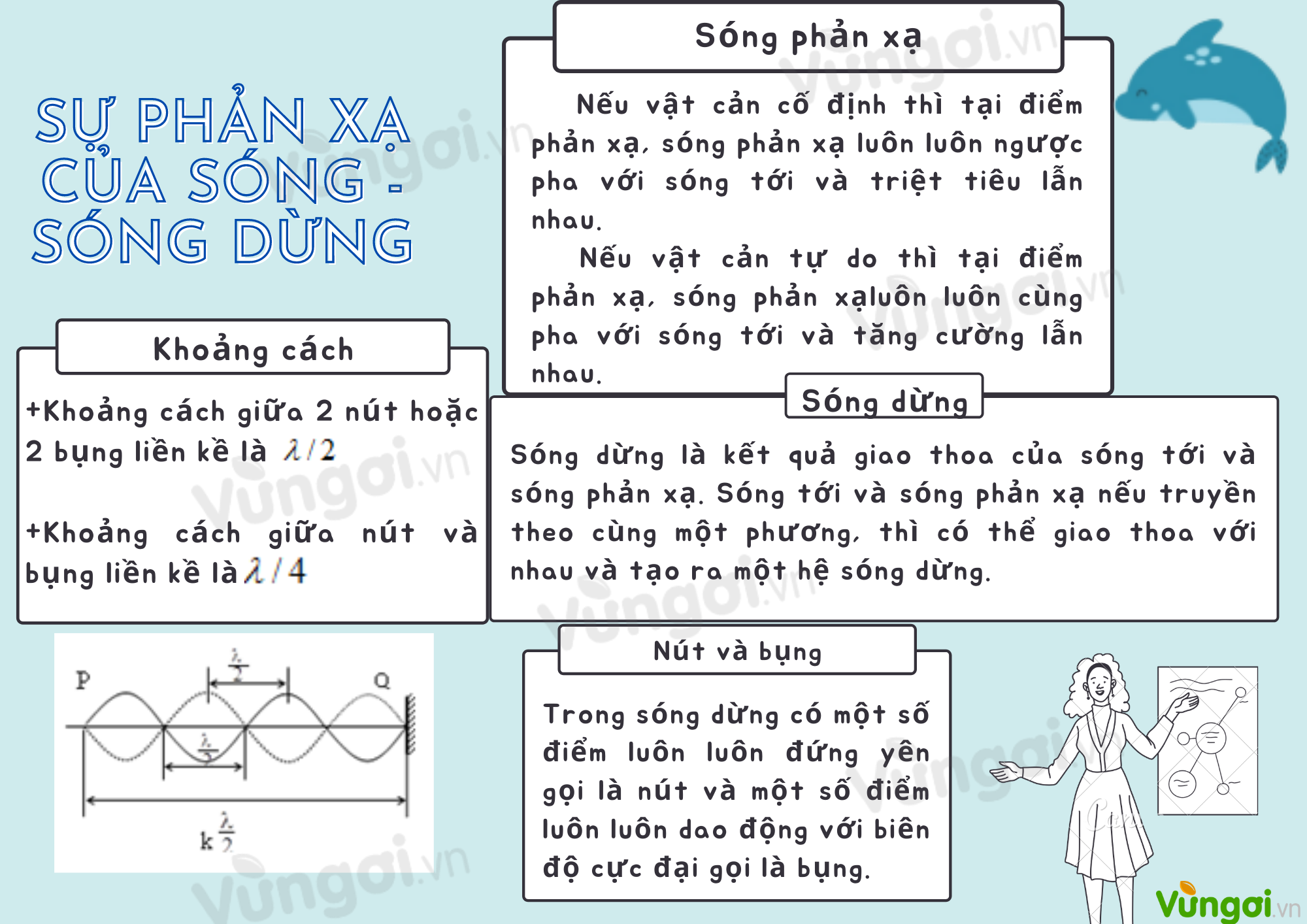
II. Sóng dừng
I- NỘI DUNG LÍ THUYẾT
1. Sự phản xạ của sóng - Sóng dừng.
- Sóng phản xạ:
- Nếu vật cản cố định thì tại điểm phản xạ, sóng phản xạ luôn luôn ngược pha với sóng tới và triệt tiêu lẫn nhau.
- Nếu vật cản tự do thì tại điểm phản xạ, sóng phản xạ luôn luôn cùng pha với sóng tới và tăng cường lẫn nhau.
- Sóng dừng là kết quả giao thoa của sóng tới và sóng phản xạ. Sóng tới và sóng phản xạ nếu truyền theo cùng một phương, thì có thể giao thoa với nhau, và tạo ra một hệ sóng dừng.
- Trong sóng dừng có một số điểm luôn luôn đứng yên gọi là nút, và một số điểm luôn luôn dao động với biên độ cực đại gọi là bụng.
- Ứng dụng: để xác định vận tốc truyền sóng.
- Khoảng cách giữa 2 nút hoặc 2 bụng liền kề của sóng dừng là \(\frac{\lambda }{2}\).
- Khoảng cách giữa nút và bụng liền kề là \(\frac{\lambda }{4}\) .
- Khoảng cách giữa hai nút (bụng, múi) sóng bất kỳ là : \(k\frac{\lambda }{2}\)
- Tốc độ truyền sóng: \(v{\rm{ }} = \lambda f{\rm{ }} = \frac{\lambda }{T}\) .
- Trong sóng dừng bề rộng của một bụng là : \(2.{a_N} = 2.2a = 4a\) .
2. Điều kiện để có sóng dừng trên dây dài l
- Hai đầu là nút sóng:
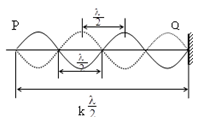
\(l = k\frac{\lambda }{2}{\rm{ }}(k \in {N^*})\)
Số bụng sóng = số bó sóng = k ; Số nút sóng = k + 1
- Một đầu là nút sóng còn một đầu là bụng sóng:
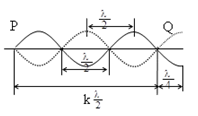
\(l = (2k + 1)\frac{\lambda }{4}{\rm{ }}(k \in N)\)
Số bó (bụng) sóng nguyên = k; Số bụng sóng = số nút sóng = k + 1
3. Phương trình sóng dừng trên dây (đầu P cố định hoặc dao động nhỏ - nút sóng)
- Đầu Q cố định (nút sóng):
- Phương trình sóng tới và sóng phản xạ tại Q:
\({u_B} = Ac{\rm{os2}}\pi ft\) và \(u{'_B} = - Ac{\rm{os2}}\pi ft = Ac{\rm{os(2}}\pi ft - \pi )\)
- Phương trình sóng tới và sóng phản xạ tại M cách Q một khoảng d là:
\({u_M} = Ac{\rm{os(2}}\pi ft + 2\pi \frac{d}{\lambda })\) và \(u{'_M} = Ac{\rm{os(2}}\pi ft - 2\pi \frac{d}{\lambda } - \pi )\)
- Phương trình sóng dừng tại M: \({u_M} = {u_M} + u{'_M}\)
\({u_M} = 2Ac{\rm{os}}(2\pi \frac{d}{\lambda } + \frac{\pi }{2})c{\rm{os}}(2\pi ft - \frac{\pi }{2}) = 2A{\rm{sin}}(2\pi \frac{d}{\lambda })c{\rm{os}}(2\pi ft + \frac{\pi }{2})\)
Biên độ dao động của phần tử tại M: \({A_M} = 2A\left| {c{\rm{os}}(2\pi \frac{d}{\lambda } + \frac{\pi }{2})} \right| = 2A\left| {{\rm{sin}}(2\pi \frac{d}{\lambda })} \right|\)
- Đầu Q tự do (bụng sóng):
- Phương trình sóng tới và sóng phản xạ tại Q: \({u_B} = u{'_B} = Ac{\rm{os2}}\pi ft\)
- Phương trình sóng tới và sóng phản xạ tại M cách Q một khoảng d là:
\({u_M} = Ac{\rm{os(2}}\pi ft + 2\pi \frac{d}{\lambda })\) và \(u{'_M} = Ac{\rm{os(2}}\pi ft - 2\pi \frac{d}{\lambda })\)
- Phương trình sóng dừng tại M: \({u_M} = {u_M} + u{'_M}\); \({u_M} = 2Ac{\rm{os}}(2\pi \frac{d}{\lambda })c{\rm{os}}(2\pi ft)\)
- Biên độ dao động của phần tử tại M: \({A_M} = 2A\left| {{\rm{cos}}(2\pi \frac{d}{\lambda })} \right|\)
* Với x là khoảng cách từ M đến đầu nút sóng thì biên độ: \({A_M} = 2A\left| {{\rm{sin}}(2\pi \frac{x}{\lambda })} \right|\)
* Với x là khoảng cách từ M đến đầu bụng sóng thì biên độ:\({A_M} = 2A\left| {{\rm{cos}}(2\pi \frac{x}{\lambda })} \right|\)
II- CÁC DẠNG BÀI TẬP
1. Dạng 1: Xác định các đại lượng đặc trưng của sóng dừng.
Phương pháp
* Hai đầu là nút sóng: \(l = k\frac{\lambda }{2}{\rm{ }}(k \in {N^*})\)
Số bụng sóng = số bó sóng = k ; Số nút sóng = k + 1
* Một đầu là nút sóng còn một đầu là bụng sóng: \(l = (2k + 1)\frac{\lambda }{4}{\rm{ }}(k \in N)\)
Số bó (bụng) sóng nguyên = k; Số bụng sóng = số nút sóng = k + 1
*Tốc độ truyền sóng: \(v{\rm{ }} = \lambda f{\rm{ }} = \frac{\lambda }{T}\)
2. Dạng 2: Xác định vận tốc, ly độ, biên độ dao động điều hòa trong sóng dừng.
Phương pháp
Phương trình sóng dừng trên sợi dây (đầu P cố định hoặc dao động nhỏ là nút sóng)
* Đầu Q cố định (nút sóng):
Phương trình sóng tới và sóng phản xạ tại Q:
\({u_B} = Ac{\rm{os2}}\pi ft\) và \(u{'_B} = - Ac{\rm{os2}}\pi ft = Ac{\rm{os(2}}\pi ft - \pi )\)
Phương trình sóng tới và sóng phản xạ tại M cách Q một khoảng d là:
\({u_M} = Ac{\rm{os(2}}\pi ft + 2\pi \frac{d}{\lambda })\) và \(u{'_M} = Ac{\rm{os(2}}\pi ft - 2\pi \frac{d}{\lambda } - \pi )\)
Phương trình sóng dừng tại M: \({u_M} = {u_M} + u{'_M}\)
\({u_M} = 2Ac{\rm{os}}(2\pi \frac{d}{\lambda } + \frac{\pi }{2})c{\rm{os}}(2\pi ft - \frac{\pi }{2}) = 2A{\rm{sin}}(2\pi \frac{d}{\lambda })c{\rm{os}}(2\pi ft + \frac{\pi }{2})\)
Biên độ dao động của phần tử tại M: \({A_M} = 2A\left| {c{\rm{os}}(2\pi \frac{d}{\lambda } + \frac{\pi }{2})} \right| = 2A\left| {{\rm{sin}}(2\pi \frac{d}{\lambda })} \right|\)
* Đầu Q tự do (bụng sóng):
Phương trình sóng tới và sóng phản xạ tại Q: \({u_B} = u{'_B} = Ac{\rm{os2}}\pi ft\)
Phương trình sóng tới và sóng phản xạ tại M cách Q một khoảng d là:
\({u_M} = Ac{\rm{os(2}}\pi ft + 2\pi \frac{d}{\lambda })\) và \(u{'_M} = Ac{\rm{os(2}}\pi ft - 2\pi \frac{d}{\lambda })\)
Phương trình sóng dừng tại M: \({u_M} = {u_M} + u{'_M}\) ; \({u_M} = 2Ac{\rm{os}}(2\pi \frac{d}{\lambda })c{\rm{os}}(2\pi ft)\)
Biên độ dao động của phần tử tại M: \({A_M} = 2A\left| {{\rm{cos}}(2\pi \frac{d}{\lambda })} \right|\)
* Công thức tính biên độ dao động của 1 phần tử tại P cách 1 nút sóng đoạn d : \({A_P} = 2A\left| {\sin (2\pi \frac{d}{\lambda }} \right|\)
* Với x là khoảng cách từ M đến đầu nút sóng thì biên độ: \({A_M} = 2A\left| {{\rm{sin}}(2\pi \frac{x}{\lambda })} \right|\)
* Với x là khoảng cách từ M đến đầu bụng sóng thì biên độ: \({A_M} = 2A\left| {{\rm{cos}}(2\pi \frac{x}{\lambda })} \right|\)
* Tốc độ truyền sóng: \(v{\rm{ }} = \lambda f{\rm{ }} = \frac{\lambda }{T}\)
