Phương pháp giải bài tập mạch xoay chiều RLC - pha u, i - viết u, i

Đối với mạch chỉ có L, C thì u vuông pha với i

\({\left( {\frac{{{u_L}}}{{{U_{0L}}}}} \right)^2} + {\left( {\frac{i}{{{I_0}}}} \right)^2} = 1\)

2. PHA U, I - VIẾT PHƯƠNG TRÌNH U, I

Cách 1: Phương pháp đại số

Ta có: \(R = 50\Omega ;{Z_L} = \omega L = 100\Omega ;{Z_C} = \frac{1}{{\omega C}} = 50\Omega  \to Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}}  = 50\sqrt 2 \Omega \)

\({U_0} = {I_0}Z = 5.50\sqrt 2  = 250\sqrt 2 V\)

\(\tan \varphi  = \frac{{{Z_L} - {Z_C}}}{R} = \frac{{100 - 50}}{{50}} = 1 \to \varphi  = \frac{\pi }{4} \to {\varphi _u} = {\varphi _i} + \frac{\pi }{4}\)

\( \to u = 250\sqrt 2 {\rm{cos(100}}\pi {\rm{t + }}\frac{\pi }{4})V\)

Cách 2: Phương pháp sử dụng casio

Với máy fx570ES : 

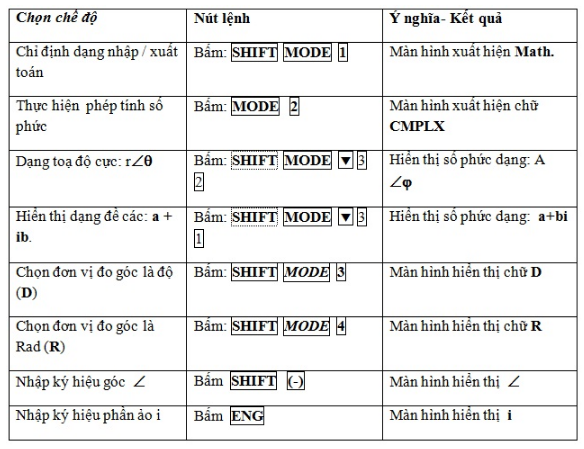
• Bước 1: Bấm  MODE 2  màn hình xuất hiện: CMPLX.
• Bước 2: Bấm  SHIFT MODE \( \vee \) 3 2 :  dạng hiển thị toạ độ cực:( r∠Θ )
• Bước 3: Chọn đơn vị đo góc là độ (D) hoặc rad (R) , bấm: SHIFT MODE 3 (hoặc 4 - rad)  màn hình hiển thị  D hoặc R
• Bước 4: Nhập liệu

 Ta có: u=i\(\overline Z \)=I₀∠φ_iX(R+(Z_L−Z_C))i=5∠0X(50+50i)     ( Phép NHÂN hai số phức)

  Nhập máy: 5 SHIFT (-)  0   X   ( 50  +  50   ENG i )

• Bước 5: Gọi kết quả: Shift 2 3 = \(353.55339\angle 45 = 250\sqrt 2 \angle 45\)

Vậy biểu thức tức thời điện áp của  hai đầu mạch:

\(u = 250\sqrt 2 {\rm{cos(100}}\pi {\rm{t + }}\frac{\pi }{4})V\)

Cách 1: Phương pháp đại số

Ta có: \(R = 40\Omega ;{Z_L} = \omega L = 100\Omega ;{Z_C} = \frac{1}{{\omega C}} = 60\Omega  \to Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}}  = 40\sqrt 2 \Omega \)

\({I_0} = \frac{{{U_0}}}{Z} = \frac{{100\sqrt 2 }}{{40\sqrt 2 }} = 2,5A\)

\(\tan \varphi  = \frac{{{Z_L} - {Z_C}}}{R} = \frac{{100 - 40}}{{40}} = 1 \to \varphi  = \frac{\pi }{4} \to {\varphi _i} = {\varphi _u} - \frac{\pi }{4}\)

\( \to i = 2,5{\rm{cos(100}}\pi {\rm{t - }}\frac{\pi }{4})V\)

Cách 2: Phương pháp sử dụng casio

Với máy fx570ES : 

• Bấm  MODE 2  màn hình xuất hiện: CMPLX.
• Bấm  SHIFT MODE 3 2 :  dạng hiển thị toạ độ cực:( r∠Θ )
• Chọn đơn vị đo góc là độ (D), bấm: SHIFT MODE 3  màn hình hiển thị  D

  Ta có: \(i = \frac{u}{{\overline Z }} = \frac{{{U_0}\angle {\varphi _u}}}{{(R + ({Z_L} - {Z_C})i)}} = \frac{{100\sqrt 2 \angle 0}}{{40 + 40i}}\)  ( Phép CHIA hai số phức)

  Nhập máy: \(100\sqrt 2 \)SHIFT (-)  0   :   ( 40  +  40   ENG i ) = 

• Gọi kết quả: Shift 2 3 = Hiển thị: \(2,5\angle  - 45\)

Vậy biểu thức tức thời điện áp của  hai đầu mạch:

\(i = 2,5{\rm{cos(100}}\pi {\rm{t - }}\frac{\pi }{4})V\)