Phương pháp giải bài tập về cường độ dòng quang điện bão hòa và hiệu suất lượng tử

Phương pháp giải bài tập về cường độ dòng quang điện bão hòa và hiệu suất lượng tử MÔN LÝ Lớp 12 với nhiều phương pháp giải nhanh kèm bài tập vận dụng
(413) 1377 26/07/2022
Bài viết đã được lưu

Nội dung bài viết

    Xem thêm

    I - NỘI DUNG

    1. Các định luật quang điện

    - Định luật quang điện thứ nhất (Định luật về giới hạn quang điện): Hiện tượng quang điện chỉ xảy ra khi ánh sáng kích thích chiếu vào kim loại có bước sóng nhở hơn hoặc bằng giới hạn quang điệnλ0 .

    - Định luật quang điện thứ hai (Định luật về cường độ dòng quang điện bão hòa): Đối với mỗi ánh sáng thích hợp (có λ≤λ0 ) cường độ dòng quang điện bão hòa tỉ lệ với cường độ của chùm sáng kích thích.

    - Định luật quang điện thứ ba (Định luật về động năng cực đại của quang electron): Động năng ban đầu cực đại của quang electron không phụ thuộc cường độ của chùm sáng kích thích, mà chỉ phụ thuộc bước sóng ánh sáng kích thích và bản chất của kim loại.

    2. Tế bào quang điện - các công thức liên quan.

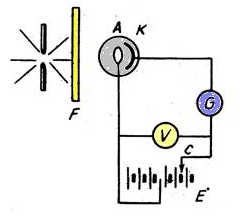
    Đặt một hiệu điện thế UAK vào hai điện cực của tế bào quang điện

    UAK có thể thay đổi giá trị (âm, dương hoặc bằng 0) tùy theo vị trí của con chạy C.

    Chiếu ánh sáng đơn sắc vào catốt của tế bào quang điện và điều chỉnh giá trị của UAK người ta thu được đường đặc trưng Vôn - Ampe của tế bào quang điện.

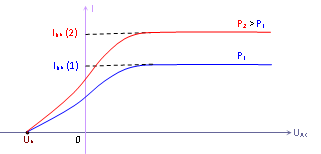
    => Điều này và một số thí nghiệm khác cho ra kết luận tương ứng với định luật quang điện thứ hai và thứ ba.

    Các công thức:

    • Công thức Anhxtanh về hiện tượng quang điện: ε=hf=A+Wd0(max)=A+12mv2max
    • Công thức tính động năng ban đầu cực đại của quang electron: Wd0(max)=12mv2max=e|Uh|

    →ε=A+12mv2max=A+e|Uh|

    II - BÀI TẬP - PHƯƠNG PHÁP GIẢI

    Xét một nguồn sáng đơn sắc có bước sóng λ, công suất P được chiếu vào catốt của một tế bào quang điện có giới hạn quang điện λ0. Khi đó:

    - Năng lượng của nguồn sáng phát ra trong thời gian t:E=P.t=Npε=Nphcλ

    Trong đó: NP là số photon phát ra trong thời gian t: Np=Ptε=Pλhct

    - Số photon của nguồn sáng phát ra trong 1s là: np=Npt=Pε=Pλhc

    - Cường độ dòng quang điện bão hòa là:Ibh=qt=Ne.et=ne.e

    Trong đó

    • q là điện lượng chuyển từ catốt sáng anốt
    • Ne là số electron bứt khỏi catốt trong thời gian t
    • ne là số electron bứt ra khỏi catốt trong 1s: ne=Net=Ibhe

    - Hiệu suất lượng tử: H=nenp100%=Ibh.hcPλe100%

    - Khi electron chuyển động trong điện trường: |e||Uh|=12mv2max=|e|Ed

    Với U là hiệu điện thế giữa anốt và catốt, vA là vận tốc cực đại của electron khi đập vào anốt, vK=vmax là vận tốc ban đầu cực đại của electron khi rời catốt thì: |eU|=12mv2A−12mv2K

    Quãng đường chuyển động mà electron đi được: Wdmax=Fsmax=qEsmax=eUdsmax

    Xem toàn bộ nội dung Vật lý 12:

    (413) 1377 26/07/2022
    Bài viết đã được lưu
    Bài trước
    Bài sau  
    Tìm thêm: Lý thuyết Lý Thuyết Lớp 12 Vật lý 12