Lý thuyết
Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Công thức
Công thức Toán học
Soạn văn
Toán THPT
Toán THCS
Thi vào lớp 10
Tuyển sinh
Đại học
Bản tin
Thư viện câu hỏi
Thi Online
Hỏi bàiPhương pháp giải bài tập năng lượng của con lắc lò xo
I. Sơ đồ năng lượng của con lắc lò xo
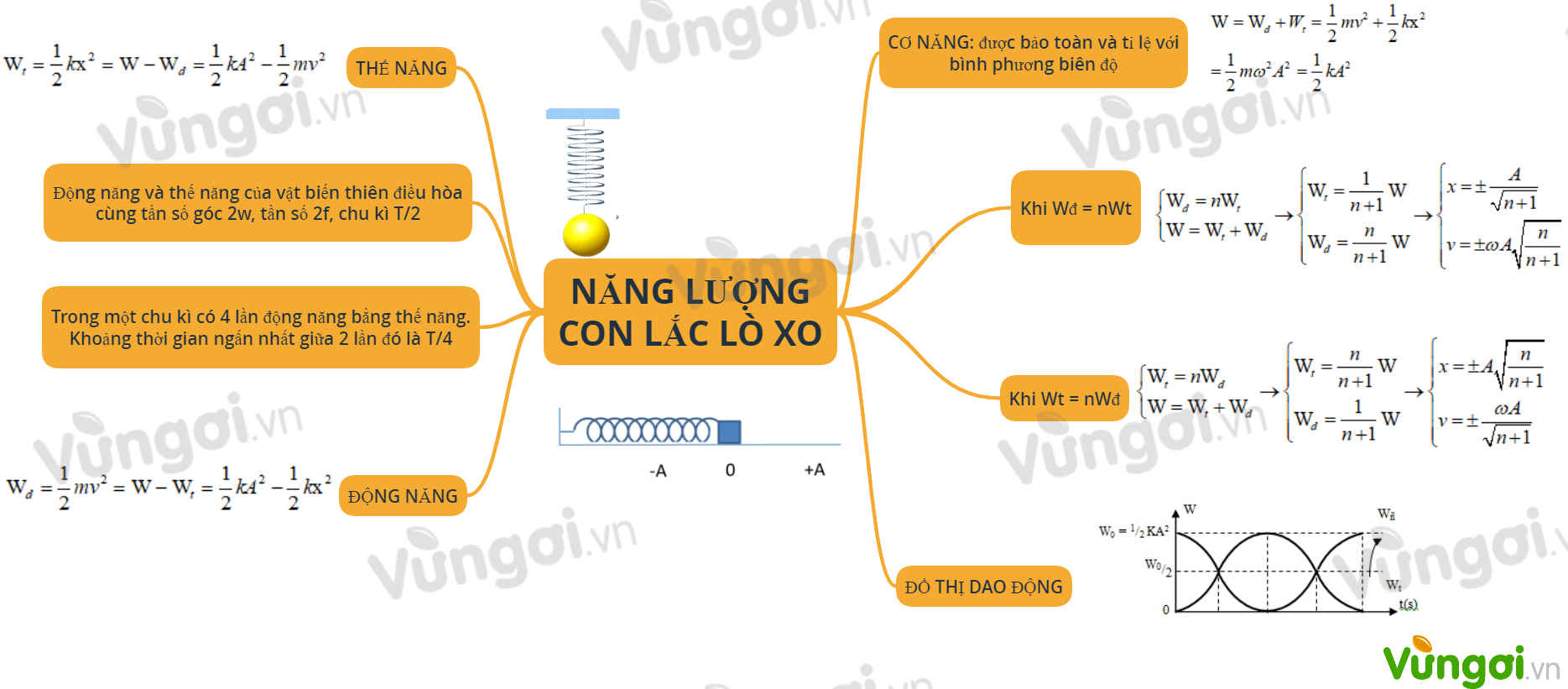
II. Phương pháp giải bài tập năng lượng của con lắc lò xo
PHƯƠNG PHÁP
Cho một con lắc lò xo có độ cứng k, vật có khối lượng m, dao động điều hòa với phương trình : \(x = Ac{\rm{os(}}\omega {\rm{t + }}\varphi {\rm{)}}\) và có vận tốc: \(v = - A\omega \sin (\omega t + \varphi )\).
- Cơ năng: \(W = {W_d} + {W_t} = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}k{x^2} = \dfrac{1}{2}m{\omega ^2}{A^2} = \dfrac{1}{2}k{A^2}\)
- Thế năng:
\(\begin{array}{l}{W_t} = \dfrac{1}{2}k{x^2} = \dfrac{1}{2}k{A^2}{\rm{co}}{{\rm{s}}^2}(\omega t + \varphi )\\ = W - {W_d} = \dfrac{1}{2}k{A^2} - \dfrac{1}{2}m{v^2}\end{array}\)
- Động năng:
\(\begin{array}{l}{W_d} = \dfrac{1}{2}m{v^2} = \dfrac{1}{2}m{\omega ^2}{A^2}{\sin ^2}(\omega t + \varphi )\\ = W - {W_t} = \dfrac{1}{2}k{A^2} - \dfrac{1}{2}k{x^2}\end{array}\)
- Đồ thị dao động:
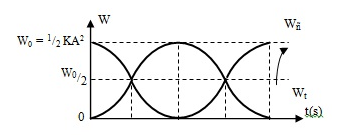
Nhận xét:
- Cơ năng được bảo toàn và tỉ lệ với bình phương biên độ.
- Vị trí thế năng cực đại thì động năng cực tiểu và ngược lại.
- Động năng và thế năng của vật biến thiên điều hòa với cùng tần số góc \(2ω\), tần số \(2f\) và chu kì \(\dfrac{T}{2}\).
- Trong 1 chu kì: có 4 lần động năng bằng thế năng. Khoảng thời gian ngắn nhất giữa hai lần động năng bằng thế năng là \(\dfrac{T}{4}\).
- Xác định vận tốc- li độ:
- Vận tốc: \({W_d} = \dfrac{1}{2}m{v^2} \to v = \pm \sqrt {\dfrac{{2{W_d}}}{m}} \)
- Li độ: \({W_t} = \dfrac{1}{2}k{x^2} \to x = \pm \sqrt {\dfrac{{2{W_t}}}{k}} \)
- Khi biết thế năng tại vị trí có li độ x gấp n lần động năng của vật: Wt = nWđ
\(\left\{ \begin{array}{l}{W_t} = n{W_d}\\W = {W_t} + {W_d}\end{array} \right. \to \left\{ \begin{array}{l}{W_t} = \dfrac{n}{{n + 1}}W\\{W_d} = \dfrac{1}{{n + 1}}W\end{array} \right. \to \left\{ \begin{array}{l}x = \pm A\sqrt {\dfrac{n}{{n + 1}}} \\v = \pm \dfrac{{A\omega }}{{\sqrt {n + 1} }}\end{array} \right.\)
- Khi biết động năng tại vị trí có li độ x gấp n lần thế năng của vật: Wđ = nWt
\(\left\{ \begin{array}{l}{W_d} = n{W_t}\\W = {W_t} + {W_d}\end{array} \right. \to \left\{ \begin{array}{l}{W_t} = \dfrac{1}{{n + 1}}W\\{W_d} = \dfrac{n}{{n + 1}}W\end{array} \right. \to \left\{ \begin{array}{l}x = \pm \dfrac{A}{{\sqrt {n + 1} }}\\v = \pm A\omega \sqrt {\dfrac{n}{{n + 1}}} \end{array} \right.\)