Ôn tập chương 1 - Dao động cơ

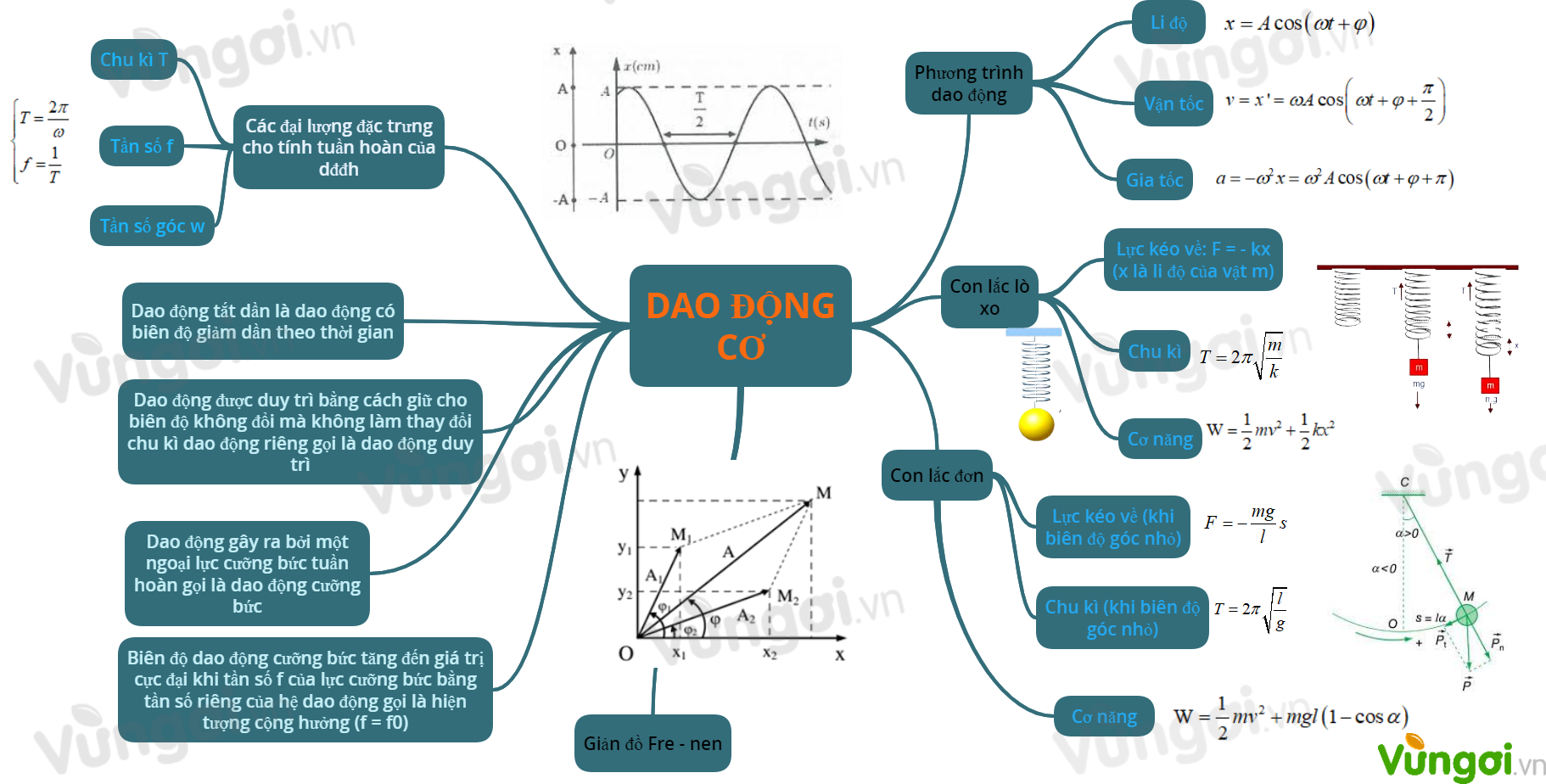
I. Sơ đồ tư duy tổng kết chương 1: Dao động cơ

II. Ôn tập chương 1: Dao động cơ

I - ĐỊNH NGHĨA VỀ DAO ĐỘNG ĐIỀU HÒA

II – CÁC ĐẠI LƯỢNG TRONG DAO ĐỘNG ĐIỀU HÒA

1. Các đại lượng dao động: x, v, a, F:

- Li độ: $x = Acos\left( {\omega t + \varphi } \right)$

- Vận tốc: $v = x' = \omega Acos\left( {\omega t + \varphi  + \dfrac{\pi }{2}} \right)$

- Gia tốc: $a = v' = x'' = {\omega ^2}Acos\left( {\omega t + \varphi  + \pi } \right)$

- Lực kéo về: $F = ma = m{\omega ^2}Acos\left( {\omega t + \varphi  + \pi } \right)$

2. Các dạng năng lượng trong dao động:

- Thế năng: ${{\rm{W}}_t} = \dfrac{1}{2}k{x^2} = \dfrac{1}{2}m{\omega ^2}{x^2}$

- Động năng: ${{\rm{W}}_d} = \dfrac{1}{2}m{v^2}$

- Cơ năng: ${\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_d} = \dfrac{1}{2}k{A^2} = \dfrac{1}{2}m{\omega ^2}{A^2} = \dfrac{1}{2}mv_{{\rm{max}}}^2$

- Khi ${{\rm{W}}_d} = n{{\rm{W}}_t} \to x =  \pm \dfrac{A}{{\sqrt {n + 1} }}$

3. Chú ý:

- Tốc độ trung bình trong một chu kì: ${v_{tb\left( T \right)}} = \dfrac{{4A}}{T} = \dfrac{{2\omega A}}{\pi } = \dfrac{{2{v_{{\rm{max}}}}}}{\pi }$

- Cứ sau khoảng thời gian ngắn nhất $\dfrac{T}{4}$ thì vật lại có ${{\rm{W}}_d} = {{\rm{W}}_t}$

III – TRỤC PHÂN BỐ THỜI GIAN

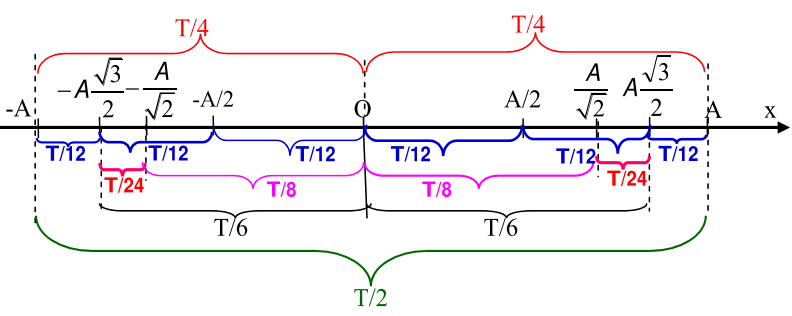
IV – QUÃNG ĐƯỜNG NHỎ NHẤT, LỚN NHẤT TRONG THỜI GIAN $\Delta t$

- Trường hợp $\Delta t < \dfrac{T}{2}$: ${S_{{\rm{max}}}} = 2A\sin \dfrac{{\omega \Delta t}}{2}$  và ${S_{\min }} = 2A\left( {1 - c{\rm{os}}\dfrac{{\omega \Delta t}}{2}} \right)$

- Trường hợp $\Delta t > \dfrac{T}{2}$ :

+ Tách $\Delta t = n\dfrac{T}{2} + \Delta t'$ trong đó $\Delta t' < \dfrac{T}{2}$

+ ${S_{{\rm{max}}}} = n.2A + {S_{{\rm{max}}\left( {\Delta t'} \right)}} = n.2A + 2A\sin \dfrac{{\omega \Delta t'}}{2}$  và ${S_{\min }} = n.2A + {S_{\min \left( {\Delta t'} \right)}} = n.2A + 2A\left( {1 - c{\rm{os}}\dfrac{{\omega \Delta t'}}{2}} \right)$ 

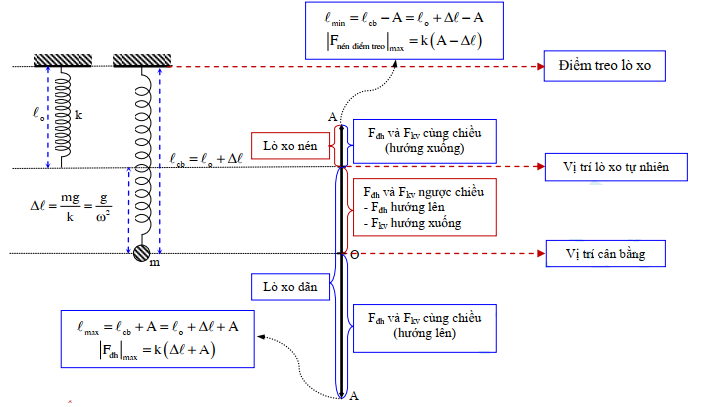
V – CON LẮC LÒ XO TREO THẲNG ĐỨNG

VI – CON LẮC ĐƠN

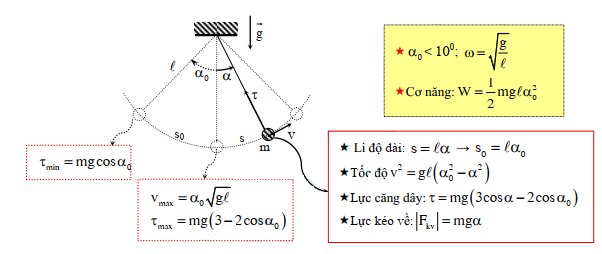
Con lắc đơn chịu tác dụng của ngoại lực:

VII – TỔNG HỢP DAO ĐỘNG ĐIỀU HÒA

${x_1} = A\cos \left( {\omega t + {\varphi _1}} \right),{x_2} = A\cos \left( {\omega t + {\varphi _2}} \right)$

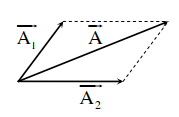
+ Biên độ dao động tổng hợp: ${A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}{\rm{cos}}\left( {{\varphi _2} - {\varphi _1}} \right)$

Điều kiện biên độ: $\left| {{A_1} - {A_2}} \right| \le A \le {A_1} + {A_2}$

+ Pha: $\tan \varphi  = \dfrac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}{\rm{cos}}{\varphi _1} + {A_2}{\rm{cos}}{\varphi _2}}}$ $\left( {{\varphi _1} \le \varphi  \le {\varphi _2}} \right)$