Con lắc lò xo - Bài tập chu kì, tần số, tần số góc của con lắc lò xo

Lý thuyết về con lắc lò xo - bài tập chu kì, tần số, tần số góc của con lắc lò xo môn lý lớp 12 với nhiều dạng bài cùng phương pháp giải nhanh kèm bài tập vận dụng
(422) 1407 26/07/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    I. Sơ đồ tổng hợp lý thuyết

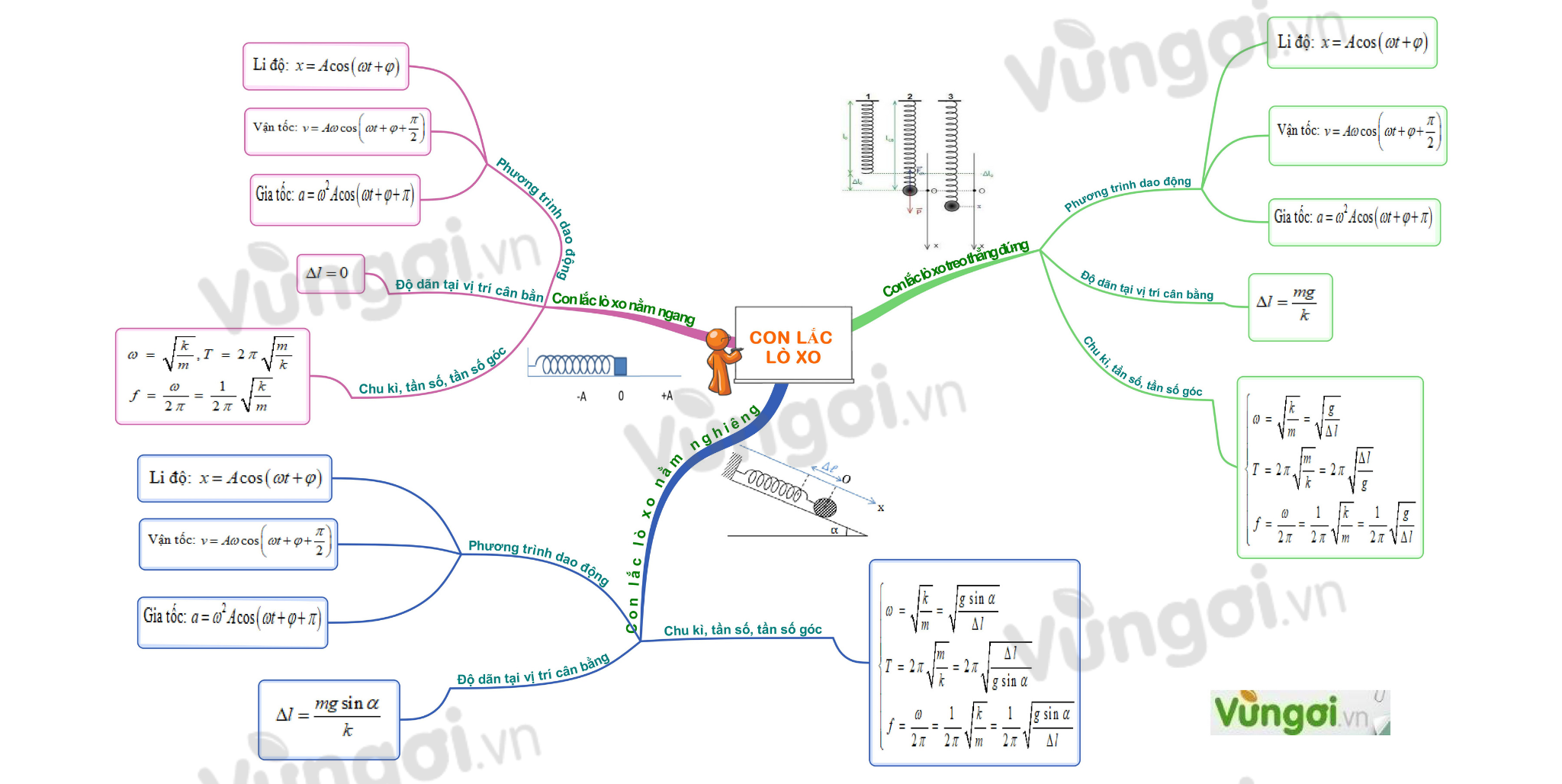
    II. Con lắc lò xo - Bài tập chu kì, tần số, tần số góc của con lắc lò xo

    I- NỘI DUNG LÍ THUYẾT

    Con lắc lò xo gồm: một vật nhỏ có khối lượng m gắn vào đầu của một lò xo có độ cứng k và có khối lượng không đáng kể, đầu kia của lò xo được giữa cố định.

    II- CÁC DẠNG BÀI TẬP

    1. Dạng 1: Xác định độ dãn của lò xo tại vị trí cân bằng.

    • Con lắc lò xo nằm ngang: \(\Delta l = 0\)
    • Con lắc lò xo treo thẳng đứng: \(\Delta l = \frac{{mg}}{k}\)
    • Con lắc lò xo nằm nghiêng: \(\Delta l = \frac{{mg\sin \alpha }}{k}\)

    2. Dạng 2: Xác định chu kì - tần số - tần số góc của con lắc lò xo

    • Con lắc lò xo nằm ngang:
    • \(\omega = \sqrt {\frac{k}{m}} ,T = \frac{{2\pi }}{\omega } = 2\pi \sqrt {\frac{m}{k}} ,f = \frac{\omega }{{2\pi }} = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} \)
    • Con lắc lò xo treo thẳng đứng:\(\omega  = \sqrt {\frac{k}{m}}  = \sqrt {\frac{g}{{\Delta l}}} ,T = 2\pi \sqrt {\frac{m}{k}}  = 2\pi \sqrt {\frac{{\Delta l}}{g}} ,{\rm{f}} = \frac{\omega }{{2\pi }} = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}}  = \frac{1}{{2\pi }}\sqrt {\frac{g}{{\Delta l}}} \)
    • Con lắc lò xo nằm nghiêng:\(\omega  = \sqrt {\frac{k}{m}}  = \sqrt {\frac{{g\sin \alpha }}{{\Delta l}}} ,T = 2\pi \sqrt {\frac{m}{k}}  = 2\pi \sqrt {\frac{{\Delta l}}{{g\sin \alpha }}} ,{\rm{ f}} = \frac{\omega }{{2\pi }} = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}}  = \frac{1}{{2\pi }}\sqrt {\frac{{g\sin \alpha }}{{\Delta l}}} \)

    3. Dạng 3: Sự thay đổi chu kì - tần số - tần số góc theo khối lượng vật nặng:

    Phương pháp:

    Gắn lò xo k vào vật khối lượng m1 được chu kỳ T1, vào vật khối lượng m2 được T2, vào vật khối lượng  m1+m2 được chu kỳ T3, vào vật khối lượng m1 – m2 (m1 > m2) được chu kỳ T4.

    Ta có: \(T = 2\pi \sqrt {\frac{m}{k}}  \to {T^2} \sim m\)

    => \(T_3^2 = T_1^2 + T_2^2 \to \left\{ \begin{array}{l}\frac{1}{{{f_3}^2}} = \frac{1}{{f_1^2}} + \frac{1}{{f_2^2}}\\\frac{1}{{{\omega _3}^2}} = \frac{1}{{\omega _1^2}} + \frac{1}{{\omega _2^2}}\end{array} \right.\) và \(T_4^2 = T_1^2 - T_2^2 \to \left\{ \begin{array}{l}\frac{1}{{{f_4}^2}} = \frac{1}{{f_1^2}} - \frac{1}{{f_2^2}}\\\frac{1}{{{\omega _4}^2}} = \frac{1}{{\omega _1^2}} - \frac{1}{{\omega _2^2}}\end{array} \right.\)

    4. Dạng 4: Chu kì, tần số, tần số góc của vật khi cắt - ghép lò xo.

    Phương pháp:

    Ta có: \(T = 2\pi \sqrt {\frac{m}{k}}  \to {T^2} \sim \frac{1}{k}\)

    Ghép lò xo:

    • Nối tiếp \(\frac{1}{k} = \frac{1}{{{k_1}}} + \frac{1}{{{k_2}}} + ...\) Þ cùng treo một vật khối lượng như nhau thì:

    \({T^2} = T_1^2 + T_2^2 + ... \to \left\{ \begin{array}{l}\frac{1}{{{f^2}}} = \frac{1}{{f_1^2}} + \frac{1}{{f_2^2}} + ...\\\frac{1}{{{\omega ^2}}} = \frac{1}{{\omega _1^2}} + \frac{1}{{\omega _2^2}} + ...\end{array} \right.\)

    • Song song: k = k1 + k2 + … Þ cùng treo một vật khối lượng như nhau thì:

    \(\frac{1}{{{T^2}}} = \frac{1}{{T_1^2}} + \frac{1}{{T_2^2}} + ... \to \left\{ \begin{array}{l}{f^2} = f_1^2 + f_2^2 + ...\\{\omega ^2} = \omega _1^2 + \omega _2^2 + ...\end{array} \right.\)

    Cắt lò xo: Một lò xo có độ cứng k, chiều dài l được cắt thành các lò xo có độ cứng k1, k2, … và chiều dài tương ứng là l1, l2, … thì có: kl = k1l1 = k2l2 = …

    Xem toàn bộ nội dung Vật lý 12:

    (422) 1407 26/07/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý Thuyết Lớp 12 Vật lý 12