Phương pháp giải bài tập về pha dao động tại một điểm trong trường giao thoa

1. DẠNG 1: XÁC ĐỊNH TẠI VỊ TRÍ ĐIỂM M DAO ĐỘNG CÙNG PHA HOẶC NGƯỢC PHA VỚI NGUỒN.

Phương pháp

Xét hai nguồn cùng pha:

Cách 1: Dùng phương trình sóng.

Gọi M là điểm dao động ngược pha với nguồn

Phương trình sóng tổng hợp tại M là: ${u_M} = 2acos(\pi \frac{{{d_2} - {d_1}}}{\lambda })cos(20\pi t - \pi \frac{{{d_2} + {d_1}}}{\lambda })$

- Nếu M dao động cùng pha với S₁, S₂ thì: $\pi \frac{{{d_2} + {d_1}}}{\lambda } = 2k\pi$

Suy ra: ${d_2} + {d_1} = 2k\lambda$ .Với ${d_1} = {\rm{ }}{d_{2}}$ ta có:    ${d_2} = {d_1} = k\lambda$

Gọi x là khoảng cách từ M đến AB: ${d_1} = {\rm{ }}{d_2} = \sqrt {{x^2} + {{\left( {\frac{{{S_1}{S_2}}}{2}} \right)}^2}}  = k\lambda$

=> Rồi suy ra x

- Nếu M dao động ngược pha với S₁, S₂ thì: $\pi \frac{{{d_2} + {d_1}}}{\lambda } = (2k + 1)\pi$

Suy ra: ${d_2} + {d_1} = \left( {2k + 1} \right)\lambda$ . Với ${d_1} = {\rm{ }}{d_{2}}$ta có: ${d_2} = {d_1} = \left( {2k + 1} \right)\frac{\lambda }{2}$

Gọi x là khoảng cách từ M đến AB: ${d_1} = {\rm{ }}{d_2} = \sqrt {{x^2} + {{\left( {\frac{{{S_1}{S_2}}}{2}} \right)}^2}}  = \left( {2k + 1} \right)\frac{\lambda }{2}$

=> Rồi suy ra x

Cách 2: Giải nhanh:          

  Ta có:      $k = \left( {\frac{{{S_1}{S_2}}}{{2\lambda }}} \right)$ (lấy phần nguyên)

- Tìm điểm cùng pha gần nhất: k +  1

- Tìm điểm ngược pha gần nhất: k +  0.5  

- Tìm điểm cùng pha thứ    n: k +  n

- Tìm điểm ngược pha thứ n : k + n - 0.5

Sau đó,  ta tính:$k\lambda  = d$.

Khoảng cách cần tìm: $x = OM{\rm{ }} = \sqrt {{d^2} - {{\left( {\frac{{{S_1}{S_2}}}{2}} \right)}^2}}$

2. DẠNG 2: XÁC ĐỊNH SỐ ĐIỂM DAO ĐỘNG CÙNG PHA, NGƯỢC PHA VỚI NGUỒN TRÊN 1 ĐOẠN THẲNG.

Phương pháp

Cách 1: Phương trình sóng tại 2 nguồn cùng biên độ A:(Điểm M cách hai nguồn lần lượt d₁, d₂)

${u_1} = {\rm{Acos}}(2\pi ft + {\varphi _1})$ và ${u_2} = {\rm{Acos}}(2\pi ft + {\varphi _2})$

+Phương trình sóng tại M do hai sóng từ hai nguồn truyền tới:

${u_{1M}} = {\rm{Acos}}(2\pi ft - 2\pi \frac{{{d_1}}}{\lambda } + {\varphi _1})$ và ${u_{2M}} = {\rm{Acos}}(2\pi ft - 2\pi \frac{{{d_2}}}{\lambda } + {\varphi _2})$

+Phương trình giao thoa sóng tại M: ${u_M} = {\rm{ }}{u_{1M}} + {\rm{ }}{u_{2M}}$

${u_M} = 2Ac{\rm{os}}\left( {\pi \frac{{{d_1} - {d_2}}}{\lambda } + \frac{{\Delta \varphi }}{2}} \right)c{\rm{os}}\left( {2\pi ft - \pi \frac{{{d_1} + {d_2}}}{\lambda } + \frac{{{\varphi _1} + {\varphi _2}}}{2}} \right)$

Pha ban đầu sóng tại M : ${\varphi _M} =  - \pi \frac{{{d_1} + {d_2}}}{\lambda } + \frac{{{\varphi _1} + {\varphi _2}}}{2}$

Pha ban đầu sóng tại nguồn S₁ hay S₂ : ${\varphi _{S1}} = {\varphi _1}$ hay ${\varphi _{S2}} = {\varphi _2}$

Độ lệch pha giữa 2 điểm M và nguồn S₁ (hay S₂ )

$\Delta \varphi  = {\varphi _{S1}} - {\varphi _M} = {\varphi _1} + \pi \frac{{{d_1} + {d_2}}}{\lambda }$ 

$\Delta \varphi  = {\varphi _{S2}} - {\varphi _M} = {\varphi _2} + \pi \frac{{{d_1} + {d_2}}}{\lambda }$

Để điểm M  dao động cùng pha với nguồn 1:$\Delta \varphi  = k2\pi  = {\varphi _1} + \pi \frac{{{d_1} + {d_2}}}{\lambda }$

 => ${d_1} + {d_2} = 2k\lambda  - \frac{{{\varphi _1}\lambda }}{\pi }$

Để điểm M dao động ngược pha với nguồn 1:$\Delta \varphi  = (2k + 1)\pi  = {\varphi _1} + \pi \frac{{{d_1} + {d_2}}}{\lambda }$

=>${d_1} + {d_2} = (2k + 1)\lambda  - \frac{{{\varphi _1}\lambda }}{\pi }$

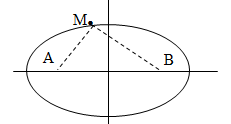
Tập hợp những điểm dao động cùng pha với 2 nguồn là họ đường Ellip nhận S₁ và S₂ làm 2 tiêu điểm.

Tập hợp những điểm dao động ngược pha với 2 nguồn là họ đường Ellip nhận S₁ và S₂ làm 2 tiêu điểm xen kẻ với họ đường Ellip trên

Cách 2: Phương pháp  nhanh :

Xác định số điểm cùng pha, ngược pha với nguồn S₁S₂  giữa 2 điểm MN trên đường trung trực

Ta có: $k = \left( {\frac{{{S_1}{S_2}}}{{2\lambda }}} \right)$

${d_{M}} = \sqrt {O{M^2} + {{\left( {\frac{{{S_1}{S_2}}}{2}} \right)}^2}}$ ;   ${d_N} = \sqrt {O{N^2} + {{\left( {\frac{{{S_1}{S_2}}}{2}} \right)}^2}}$ 

- Cùng pha khi:   ${k_M} = \frac{{{d_M}}}{\lambda }$   ;                   ${k_N} = \frac{{{d_N}}}{\lambda }$          

- Ngược pha khi: ${k_M} + 0,5 = \frac{{{d_M}}}{\lambda }$  ;   ${k_N} + 0,5 = \frac{{{d_N}}}{\lambda }$       

 Từ  k  và  k_M  =>   số điểm trên  OM

 Từ  k  và  k_N  =>  số điểm trên  ON

=>  số điểm trên MN ( cùng phía thì trừ, khác phía thì cộng)