Phương pháp giải tập chiều dài CLLX - Lực đàn hồi, lực hồi phục của CLLX

Phương pháp giải bài tập chiều dài CLLX - lực đàn hồi, lực hồi phục của con lắc lò xo MÔN LÝ Lớp 12 với nhiều phương pháp giải nhanh kèm bài tập vận dụng
(402) 1340 26/07/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    I. Phương pháp giải bài tập chiều dài CLLX - lực đàn hồi, lực hồi phục của con lắc lò xo

    CÁC DẠNG BÀI TẬP - PHƯƠNG PHÁP GIẢI

    1. Dạng 1: Tính chiều dài của lò xo trong quá trình vật dao động

    Gọi chiều dài tự nhiên của lò xo là l0.

    - Khi con lắc lò xo nằm ngang:

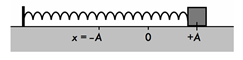
    + Lúc vật ở VTCB, lò xo không bị biến dạng, 

    + Chiều dài cực đại của lò xo: \({l_{{\rm{max}}}} = {l_0} + A\)

    + Chiều dài cực tiểu của lò xo: \({l_{{\rm{min}}}} = {l_0} - A\)

    + Chiều dài ở li độ x: \(l = {l_0} + x\)

    - Khi con lắc lò xo bố trí thẳng đứng hoặc nằm nghiêng một góc αvà treo ở dưới.

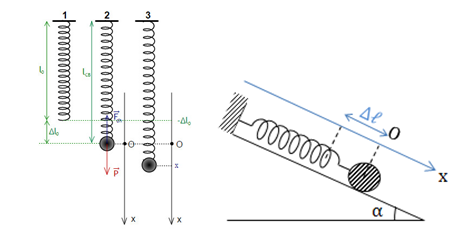
    + Độ biến dạng của lò xo khi vật ở VTCB: 

    • Con lắc lò xo treo thẳng đứng: \(\Delta {l_0} = \frac{{mg}}{k}\)
    • Con lắc lò xo nằm nghiêng góc α: \(\Delta {l_0} = \frac{{mg\sin \alpha }}{k}\)

    + Chiều dài lò xo khi vật ở VTCB: \({l_{vtcb}} = {l_0} + \Delta l\)

    + Chiều dài ở li độ x: \(l = {l_0} + \Delta {l_0} + x\)

    + Chiều dài cực đại của lò xo: \({l_{{\rm{max}}}} = {l_0} + \Delta {l_0} + A\)

    + Chiều dài cực tiểu của lò xo: \({l_{{\rm{min}}}} = {l_0} + \Delta {l_0} - A\)

    2. Dạng 2: Lực kéo về

    \(F{\rm{ }} =  - {\rm{ }}kx{\rm{ }} =  - {\rm{ }}m{\omega ^2}x\)

        Đặc điểm:

    * Là lực gây dao động cho vật.

    * Luôn hướng về VTCB

    * Biến thiên điều hoà cùng tần số với li độ

    3. Dạng 3: Lực đàn hồi - Lực hồi phục cực đại, cực tiểu.

    Có độ lớn \({F_{dh}} = {\rm{ }}k{x^*}\)  (x* là độ biến dạng của lò xo)

    - Với con lắc lò xo nằm ngang thì lực kéo về và lực đàn hồi là một (vì tại VTCB lò xo không biến dạng)

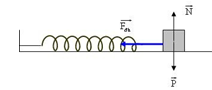
    - Với con lắc lò xo thẳng đứng hoặc đặt trên mặt phẳng nghiêng:

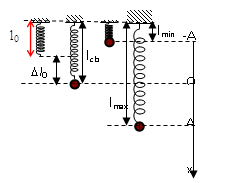
    + Độ lớn lực đàn hồi có biểu thức:

    • \({F_{dh}} = {\rm{ }}k|\Delta {l_0} + {\rm{ }}x|\) với chiều dương hướng xuống
    • \({F_{dh}} = k\left| {\Delta {l_0} - {\rm{ }}x} \right|\) với chiều dương hướng lên

    + Lực đàn hồi cực đại (lực kéo): \({F_{{\rm{max}}}} = k\left( {\Delta {l_0} + A} \right) = {F_{Km{\rm{ax}}}}\) (lúc vật ở vị trí thấp nhất)

    + Lực đàn hồi cực tiểu:

    • Nếu\(A{\rm{ }} < \Delta {l_0} \to {F_{Min}} = {\rm{ }}k(\Delta {l_0} - {\rm{ }}A) = {F_{KMin}}\)
    • Nếu \(A{\rm{ }} \ge \Delta {l_0} \to {F_{Min}} = 0\)  (lúc vật đi qua vị trí lò xo không biến dạng)

    + Lực đẩy (lực nén) đàn hồi cực đại: ${F_{Nm{\rm{ax}}}} = k\left( {A - \Delta {l_0}} \right)$ (lúc vật ở vị trí cao nhất)

    + Lực đàn hồi, lực hồi phục:

    • Lực đàn hồi:

      \(\begin{array}{l}{F_{dh}} = k(\Delta l + x){\rm{ }}\\ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{F_{d{h_{{\rm{Max}}}}}} = k(\Delta l + A){\rm{                 }}}\\{{F_{d{h_{\min }}}} = k(\Delta l - A){\rm{ khi }}\Delta l > A}\\{{F_{d{h_{\min }}}} = 0{\rm{ khi}}\Delta {\rm{l}} \le {\rm{A             }}}\end{array}} \right.{\rm{      }}\end{array}\)

    •  Lực hồi phục: \({F_{hp}} = kx{\rm{ }} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{F_{h{p_{{\rm{Max}}}}}} = kA}\\{{F_{h{p_{\min }}}} = 0{\rm{ }}}\end{array}} \right.{\rm{ }}\)hay\({F_{hp}} = ma{\rm{ }} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{F_{h{p_{{\rm{Max}}}}}} = m{\omega ^2}A}\\{{F_{h{p_{\min }}}} = 0{\rm{        }}}\end{array}} \right.\)  

    + Lực hồi phục luôn hướng vào vị trí cân bằng.

    Khi hệ dao động theo phương nằm ngang thì lực đàn hồi và lực hồi phục là như nhau ${F_{dh}} = {F_{hp}}$

    II. Bảng so sánh lực lực hồi phục và lực đàn hồi

    Xem toàn bộ nội dung Vật lý 12:

    (402) 1340 26/07/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý Thuyết Lớp 12 Vật lý 12