Phương pháp giải bài tập mạch xoay chiều RLC - có C thay đổi
1. C THAY ĐỔI => XẢY RA HIỆN TƯỢNG CỘNG HƯỞNG \({\varphi _{{\bf{U}}/{\bf{I}}}} = {\bf{0}}\) VÀ \({{\bf{I}}_{{\bf{MAX}}}},{\rm{ }}{{\bf{U}}_{{\bf{RMAX}}}},{\rm{ }}{{\bf{U}}_{{\bf{LMAX}}}},{\rm{ }}{{\bf{U}}_{{\bf{LCMIN}}}}\)
\({Z_L} = {Z_C}\)
Khi đó:
\(\begin{array}{l}{Z_{\min }} = R\\{I_{{\rm{max}}}} = \dfrac{U}{R}\\{P_{{\rm{max}}}} = {I^2}R = \dfrac{{{U^2}}}{R}\end{array}\)
+ Điện áp giữa hai đầu điện trở cực đại và bằng điện áp toàn mạch
\({U_L} = {U_C} \to U = \sqrt {U_R^2 + {{({U_L} - {U_C})}^2}} = {U_R}\)
+ Điện áp hai đầu đoạn mạch cùng pha với cường độ dòng điện trong mạch: φ=0
2. C THAY ĐỔI ĐỂ UCMAX VÀ ĐIỆN ÁP HAI ĐẦU ĐOẠN MẠCH VUÔNG PHA VỚI URL
Ta có: \({U_C} = I{Z_C} = \dfrac{{U{Z_C}}}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}\)
Chia cả tử và mẫu cho ZC, ta được: \({U_C} = \dfrac{U}{{\sqrt {\dfrac{{{R^2}}}{{{Z_C}^2}} + \frac{{{{({Z_L} - {Z_C})}^2}}}{{{Z_C}^2}}} }} = \dfrac{U}{{\sqrt {\dfrac{{{R^2} + Z_L^2}}{{{Z_C}^2}} - \dfrac{{2{Z_L}}}{{{Z_C}}} + 1} }}\)
Đặt \(y = \dfrac{{{R^2} + Z_L^2}}{{{Z_C}^2}} - \dfrac{{2{Z_L}}}{{{Z_C}}} + 1 = ({R^2} + Z_L^2){x^2} - 2{Z_L}x + 1\) với $x = \dfrac{1}{{{Z_C}}}$
Ta có UCmax khi ymin
\({y_{\min }} \leftrightarrow x = - \dfrac{b}{{2{\rm{a}}}} = \dfrac{{2{Z_L}}}{{2({R^2} + Z_L^2)}} \to {Z_C} = \dfrac{{{R^2} + Z_L^2}}{{{Z_L}}}\)
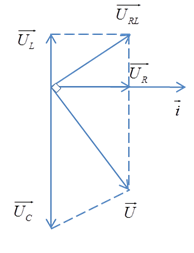
Khi đó: \({U_{Cm{\rm{ax}}}} = \dfrac{{U_R^2 + U_L^2}}{{{U_L}}} = \dfrac{{U\sqrt {{R^2} + Z_L^2} }}{R}\)
Hệ quả: \(\left\{ \begin{array}{l}{U_{RL}} \bot {U_{AB}}\\U_{C\max }^2 = {U^2} + U_{RL}^2 = {U^2} + U_R^2 + U_L^2\\U_{C\max }^{}.{U_R} = U.{U_{RL}}\\\dfrac{1}{{U_R^2}} = \dfrac{1}{{{U^2}}} + \dfrac{1}{{U_{RL}^2}}\end{array} \right.\)
3. C THAY ĐỔI ĐỂ URCMAX
Ta có: \({U_{RC}} = I{Z_{RC}} = \dfrac{{U\sqrt {{R^2} + Z_C^2} }}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \dfrac{{U\sqrt {{R^2} + Z_C^2} }}{{\sqrt {{R^2} + {Z_L}^2 - 2{Z_L}{Z_C} + {Z_C}^2} }} = \dfrac{U}{{\sqrt {1 + \dfrac{{ - 2{Z_L}{Z_C} + {Z_L}^2}}{{{R^2} + Z_C^2}}} }}\)
\({U_{RLmax}} \leftrightarrow {\left( {1 + \dfrac{{ - 2{Z_L}{Z_C} + {Z_L}^2}}{{{R^2} + Z_C^2}}} \right)_{\min }}\)
\(\begin{array}{*{20}{l}}{y = 1 + \dfrac{{ - 2{Z_L}{Z_C} + {Z_L}^2}}{{{R^2} + Z_C^2}}}\\{y' = {{(1 + \dfrac{{ - 2{Z_L}{Z_C} + {Z_L}^2}}{{{R^2} + Z_C^2}})}^\prime } = \dfrac{{2{Z_C}^2 - 2{R^2} - 2{Z_L}{Z_C}}}{{{{({R^2} + Z_C^2)}^2}}}}\\{y' = 0 \leftrightarrow 2{Z_C}^2 - 2{R^2} - 2{Z_L}{Z_C} = 0}\\{\left\{ \begin{array}{l}{Z_C} > 0\\{Z_C} = \dfrac{{ - b + \sqrt \Delta }}{{2a}} = \dfrac{{{Z_L} + \sqrt {4{R^2} + Z_L^2} }}{2}\end{array} \right.}\end{array}\)
Khi đó:
\({{U}_{RC\max }}=\frac{2UR}{\sqrt{4{{R}^{2}}+Z_{L}^{2}}-{{Z}_{L}}}\)
4. C THAY ĐỔI ĐỂ URL KHÔNG PHỤ THUỘC VÀO R
URL không phụ thuộc vào R
\( \leftrightarrow {U_{RL}} = {U_{AB}}\)
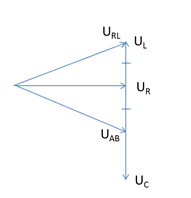
Từ giản đồ:
\(\begin{array}{l} \to {U_C} = 2{U_L}\\ \to {Z_C} = 2{Z_L}\end{array}\)
5. C THAY ĐỔI ĐỂ \({U_{RC}} \bot {U_{RL}}\)
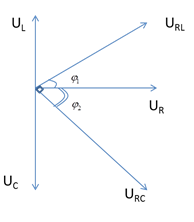
\(\begin{array}{l}{U_{RL}} \bot {U_{RC}}\\ \leftrightarrow \left\{ \begin{array}{l}\sin {\varphi _1} = c{\rm{os}}{\varphi _2}\\c{\rm{os}}{\varphi _1} = \left| {\sin {\varphi _2}} \right|\end{array} \right. \to \left| {\tan {\varphi _1}\tan {\varphi _2}} \right| = 1\\ \leftrightarrow \frac{{{U_L}}}{{{U_R}}}\frac{{{U_C}}}{{{U_R}}} = 1 \leftrightarrow {U_L}{U_C} = {U_R}^2 \leftrightarrow {Z_L}{Z_C} = {R^2}\end{array}\)
6. C=C1 HOẶC C=C2 THÌ UC CÓ CÙNG GIÁ TRỊ
\({C_1} + {C_2} = 2{C_{max}} = 2{C_0} \to {C_0} = \dfrac{{{C_1} + {C_2}}}{2}\)
7. C THAY ĐỔI CÓ 2 GIÁ TRỊ LÀM CHO: \({{\bf{I}}_{\bf{1}}} = {{\bf{I}}_{\bf{2}}},{\rm{ }}{{\bf{P}}_{\bf{1}}} = {{\bf{P}}_{\bf{2}}},{\rm{ }}{\bf{cos}}{\varphi _{\bf{1}}} = {\bf{cos}}{\varphi _{\bf{2}}},{\rm{ }}{{\bf{Z}}_{\bf{1}}} = {{\bf{Z}}_{\bf{2}}}\)
- Z1=Z2
\({R^2} + {({Z_L} - {Z_{C1}})^2} = {R^2} + {({Z_L} - {Z_{C2}})^2} \to \left| {{Z_L} - {Z_{C1}}} \right| = \left| {{Z_L} - {Z_{C2}}} \right|\)
Với ZC2>ZC1 \( \to {Z_{C1}} + {Z_{C2}} = 2{Z_L}\)
- I1=I2 hoặc P1=P2 => L=? để cộng hưởng điện
\( \leftrightarrow \left\{ \begin{array}{l}I = {I_{{\rm{max}}}}\\{\varphi _u} = {\varphi _i}\\\left| {{\rm{cos}}\varphi } \right| = 1\end{array} \right. \to 2{Z_{Cm{\rm{ax}}}} = {Z_{C1}} + {Z_{C2}}\)
