Lý thuyết
Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Công thức
Công thức Toán học
Soạn văn
Toán THPT
Toán THCS
Thi vào lớp 10
Tuyển sinh
Đại học
Bản tin
Thư viện câu hỏi
Thi Online
Hỏi bàiPhương pháp giải bài tập dao động điều hòa - Viết phương trình dao động điều hòa
I. Bảng tóm tắt các bước viết phương trình dao động điều hòa
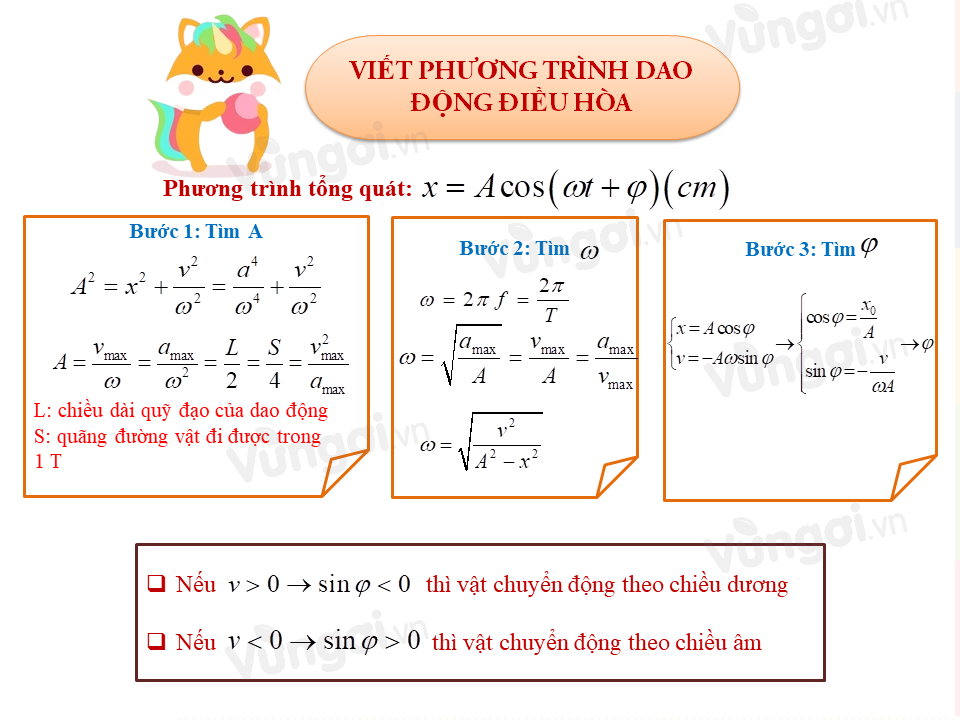
II. Phương pháp giải bài tập dao động điều hòa - Viết phương trình dao động điều hòa
I- DẠNG 1: VIẾT PHƯƠNG TRÌNH DAO ĐỘNG ĐIỀU HÒA.
1. Phương pháp.
Phương trình dao động tổng quát: \(x{\rm{ }} = {\rm{ }}Acos\left( {\omega t{\rm{ }} + {\rm{ }}\varphi } \right)\)
- Bước 1: Tìm A: $\left\{ \begin{array}{l}
A = \dfrac{{{v_{{\rm{max}}}}}}{\omega } = \dfrac{{{a_{{\rm{max}}}}}}{{{\omega ^2}}} = \dfrac{L}{2} = \dfrac{S}{4} = \dfrac{{{v_{{\rm{max}}}}^2}}{{{a_{{\rm{max}}}}}}\\
{A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {\dfrac{a}{{{\omega ^4}}}^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}
\end{array} \right.$
- L: chiều dài quỹ đạo của dao động
- S: quãng đường vật đi được trong một chu kì
- Bước 2: Tìm Tìm \(\omega\): \(\omega = \sqrt {\dfrac{k}{m}} = 2\pi f = \dfrac{{2\pi }}{T} = \sqrt {\dfrac{{{a_{{\rm{max}}}}}}{A}} = \dfrac{{{v_{{\rm{max}}}}}}{A} = \dfrac{{{a_{{\rm{max}}}}}}{{{v_{{\rm{max}}}}}} = \sqrt {\dfrac{{{v^2}}}{{{A^2} - {x^2}}}} \)
Trong đó:
- Chu kì T: \(T = \dfrac{t}{N}\)
- Tần số f: \(f = \dfrac{N}{t}\)
- N là số dao động vật thực hiện được trong khoảng thời gian t
- Bước 3: Tìm \(\varphi \)
Tại t = 0: \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\varphi \\{\rm{v = - A}}\omega {\rm{sin}}\varphi \end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\dfrac{{{x_0}}}{A}\\\sin \varphi = - \dfrac{v}{{A\omega }}\end{array} \right. \to \varphi = ?\)
- nếu \(v > 0 \to \sin \varphi < 0\) vật chuyển động theo chiều dương
- nếu \(v < 0 \to \sin \varphi > 0\) vật chuyển động theo chiều âm
Ta có thể thay đổi thứ tự các bước tùy theo tính chất đề bài.
2. Ví dụ:
|
Ví dụ 1: Một vật nhỏ dao động điều hòa theo trục Ox (VTCB là O) với biên độ 4cm và tần số 10Hz. Tại thời điểm t = 0, vật có li độ 4cm. Phương trình dao động của vật là: A. \(x = 4c{\rm{os(20}}\pi {\rm{t + }}\pi {\rm{)}}\) B. \(x = 4c{\rm{os(20}}\pi t{\rm{)}}\) C. \(x = 4c{\rm{os(}}10{\rm{t + }}\pi {\rm{)}}\) D. \(x = 4c{\rm{os(10t)}}\) |
Hướng dẫn:
Ta có:
\(A{\rm{ }} = {\rm{ }}4cm\)
\(f = 10{\rm{ }}Hz \to \omega = 2\pi f = 2\pi .10 = 20\pi {\rm{ }}ra{\rm{d}}/s\)
Tại t = 0: \(x = A \to \varphi = 0\)
=> Phương trình dao động : \(x = 4c{\rm{os(20}}\pi t{\rm{)}}\)
Chọn B
|
Ví dụ 2: Một chất điểm dao động điều hòa trên trục Ox. Trong thời gian 31,4s chất điểm thực hiện được 100 dao động thành phần. Chọn gốc thời gian lúc vật đi qua vị trí có li độ \(x = 2cm\) theo chiều âm với tốc độ \(40\sqrt 3 cm/s\). Phương trình dao động của chất điểm là: A. \(x = 0,04cos(20t + \dfrac{\pi }{3}){\rm{ }}cm\) B. \(x = 4cos(10\pi t + \dfrac{\pi }{3}){\rm{ }}cm\) C. \(x = 0,04cos(10\pi t + \dfrac{\pi }{3}){\rm{ }}cm\) D. \(x = 4cos(20t + \dfrac{\pi }{3}){\rm{ }}cm\) |
Hướng dẫn:
Chu kì: \(T = \dfrac{t}{N} = \dfrac{{31,4}}{{100}} = 0,314{\rm{s}}\)
\( \to \omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{0,314}} = 20{\rm{r}}a{\rm{d}}/s\)
Sử dụng hệ thức độc lập A-x-v:
\(\begin{array}{l}{A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {2^2} + \dfrac{{{{(40\sqrt 3 )}^2}}}{{{{20}^2}}} = 16\\ \to A = 4cm\end{array}\)
Tại t = 0: \(\left\{ \begin{array}{l}x = 2\\v < 0\end{array} \right. \to \left\{ \begin{array}{l}Ac{\rm{os}}\varphi {\rm{ = 2}}\\{\rm{sin}}\varphi {\rm{ > 0}}\end{array} \right. \to \left\{ \begin{array}{l}{\rm{cos}}\varphi {\rm{ = }}\dfrac{2}{4} = \dfrac{1}{2}\\{\rm{sin}}\varphi {\rm{ > 0}}\end{array} \right. \to \varphi = \dfrac{\pi }{3}\)
=> Phương trình dao động: \(x = 4cos(20t + \dfrac{\pi }{3}){\rm{ }}cm\)
Chọn D
II- DẠNG 2: CHO PHƯƠNG TRÌNH VẬN TỐC HOẶC GIA TỐC - TÌM PHƯƠNG TRÌNH LI ĐỘ X
1. Phương pháp:
Giả sử phương trình của v và a là: \(\left\{ \begin{array}{l}v = \omega Ac{\rm{os(}}\omega {\rm{t + }}{\varphi _v})\\a = \omega {\rm{Acos(}}\omega {\rm{t + }}{\varphi _a})\end{array} \right.\)
- Bước 1: Tìm A, ω: từ phương trình của v hoặc a.
- Bước 2: Tìm \({\varphi _x}:\left\{ \begin{array}{l}{\varphi _x} = {\varphi _v} - \frac{\pi }{2}\\{\varphi _x} = {\varphi _a} - \pi \end{array} \right.\)
(do vận tốc nhanh pha hơn x một góc \(\pi /2\) và gia tốc a ngược pha với x)
2. Ví dụ:
Cho phương trình của vận tốc là \(v = 8\pi cos(2\pi t + \frac{\pi }{3})cm/s\). Tìm phương trình của li độ x.
Hướng dẫn:
Từ phương trình vận tốc, ta có: \(\omega = 2\pi ra{\rm{d}}/s\) , \(A = \frac{{{v_{{\rm{max}}}}}}{\omega } = \frac{{8\pi }}{{2\pi }} = 4cm\)
\({\varphi _x} = {\varphi _v} - \frac{\pi }{2} = \frac{\pi }{3} - \frac{\pi }{2} = - \frac{\pi }{6}\)
=> Phương trình của li độ x: \(x = 4cos(2\pi t - \frac{\pi }{6})cm\)
III- DẠNG 3: DAO ĐỘNG CÓ PHƯƠNG TRÌNH ĐẶC BIỆT
Phương pháp:
- \(x{\rm{ }} = {\rm{ }}a \pm Acos(\omega t{\rm{ }} + \varphi )\) với a = const
- Biên độ là A
- tần số góc là \(\omega \)
- pha ban đầu \(\varphi \)
- x là toạ độ
- \({x_0} = Acos(\omega t{\rm{ }} + \varphi )\) là li độ.
- Toạ độ vị trí cân bằng \(x{\rm{ }} = {\rm{ }}a\)
- toạ độ vị trí biên \(x{\rm{ }} = {\rm{ }}a \pm A\)
- Vận tốc \(v = {\rm{ }}x' = {\rm{ }}{x_0}'\)
- gia tốc \(a{\rm{ }} = v' = x'' = {x_0}''\)
Hệ thức độc lập: \(a{\rm{ }} = - {\omega ^2}{x_0};{A^2} = x_0^2 + {(\frac{v}{\omega })^2}\)
- \(x = a \pm Aco{s^2}(\omega t{\rm{ }} + \varphi )\) (ta hạ bậc)
- Biên độ A/2
- tần số góc \(2\omega \)
- pha ban đầu \(2\varphi \)